Файл: Расчётнографическая работа по дисциплине Статистическая радиотехника вариант 1 бригада 5.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 41
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
.
Вычислим коэффициент :
:
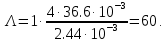
Отсюда нормированная дисперсия ошибки при использовании фильтра Винера:
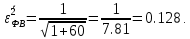
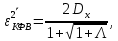
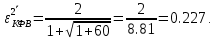
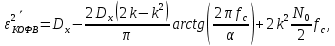
где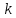 и
и 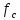 – оптимальные параметры, которые равны:
– оптимальные параметры, которые равны:
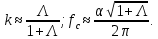
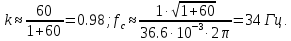
Подставим эти значения и получим нормированную дисперсию ошибки при использовании квазиоптимального фильтра Винера:
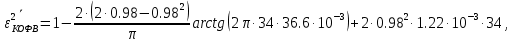
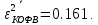

10
Задание 2:
Рассчитать зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от:
а) спектральной плотности шума при заданных в п. 1 значениях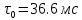 и
и  ;
;
б) интервала корреляции сигнала при заданных в п.1 значениях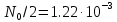 и
и  .
.
Диапазон изменения параметров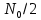 в п. 2(а) и
в п. 2(а) и 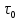 в п. 2(б) должен составлять
в п. 2(б) должен составлять 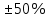 относительно значений, заданных в задании 1.
относительно значений, заданных в задании 1.
Решение:
а) Нормированная дисперсия ошибки фильтрации ФВ:
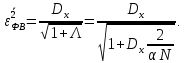
Нормированная дисперсия ошибки фильтрации КФВ:
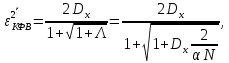
где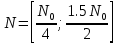 – СПМ шума в заданном диапазоне изменения
– СПМ шума в заданном диапазоне изменения  .
.
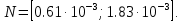
Построим график зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения СПМ шума (рис. 3.1).

11
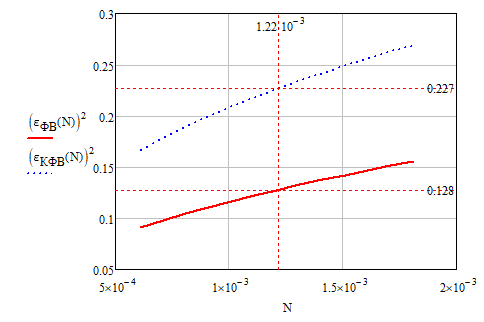
Рис. 3.1. График зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения СПМ шума
б) Нормированная дисперсия ошибки фильтрации ФВ:
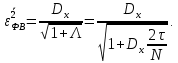
Нормированная дисперсия ошибки фильтрации КФВ:
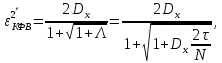
где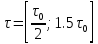 – интервал корреляции сигнала в заданном диапазоне изменения
– интервал корреляции сигнала в заданном диапазоне изменения  .
.
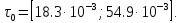
Построим график зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения интервала корреляции сигнала (рис. 3.2).

12
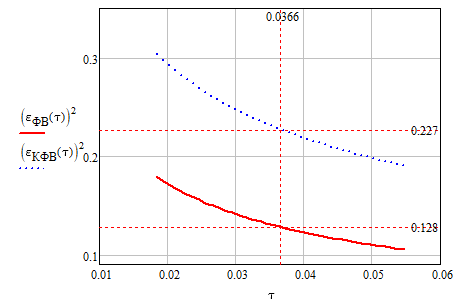
Рис. 3.2. График зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения интервала корреляции
Задание 3:
Рассчитать объём выборки (количество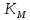 независимых реализаций), при которой относительная ошибка измерения в эксперименте величины
независимых реализаций), при которой относительная ошибка измерения в эксперименте величины  не превысит 1%. При этом приближённо принять интервал корреляции
не превысит 1%. При этом приближённо принять интервал корреляции 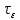 текущей ошибки фильтрации
текущей ошибки фильтрации 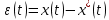 равным удвоенному интервалу корреляции
равным удвоенному интервалу корреляции 
процесса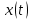 , а отсчёты, отстоящие на интервал корреляции – независимыми.
, а отсчёты, отстоящие на интервал корреляции – независимыми.
Решение:
Интервал дискретизации:

Интервал корреляции, согласно заданию, определяется как:
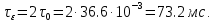

13
Длина реализации, при котором относительная ошибка измерения в эксперименте величины не превысит 1%:
не превысит 1%:
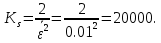
Количество отсчётов :
:
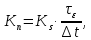
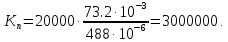
Объём выборки:
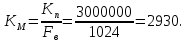
ВЫВОД: из расчётов видно, что лучшие результаты искомых параметров показывает некаузальный фильтр Винера (ФВ), так как он обеспечивает минимум нормированной дисперсии ошибки, по сравнению с квазиоптимальным и каузальным фильтрами. Но фильтр Винера физически нереализуем, что является его существенным недостатком. Это связано с тем, что некаузальный ФВ, использует все входные данные для получения оценки - от ранее поступивших до будущих. Использование прошлых данных, т. е. уже поступивших к текущему моменту времени, физически оправдано и технически реализуемо, а использование будущих данных - невозможно.
Каузальный фильтр Винера, физически реализуем и формирует оценку только за счёт ранее поступивших данных, но имеет ошибку фильтрации значительно выше, чем квазиоптимальный фильтр и фильтр Винера. Это связано с тем, что для образования оценки он использует малое количество данных, в отличие от НКФВ и КОФВ.


14
14
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ


15
15
Вычислим коэффициент
 :
: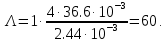
Отсюда нормированная дисперсия ошибки при использовании фильтра Винера:
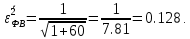
-
Нормированная дисперсия ошибки при использовании каузального фильтра Винера:
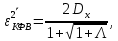
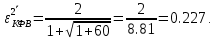
-
Нормированная дисперсия ошибки при использовании квазиоптимального фильтра Винера:
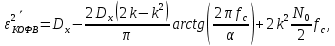
где
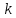 и
и 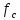 – оптимальные параметры, которые равны:
– оптимальные параметры, которые равны: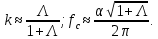
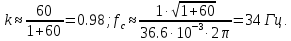
Подставим эти значения и получим нормированную дисперсию ошибки при использовании квазиоптимального фильтра Винера:
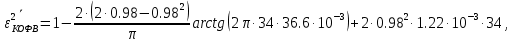
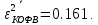

10
Задание 2:
Рассчитать зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от:
а) спектральной плотности шума при заданных в п. 1 значениях
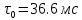 и
и  ;
;б) интервала корреляции сигнала при заданных в п.1 значениях
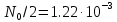 и
и  .
.Диапазон изменения параметров
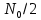 в п. 2(а) и
в п. 2(а) и 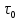 в п. 2(б) должен составлять
в п. 2(б) должен составлять 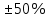 относительно значений, заданных в задании 1.
относительно значений, заданных в задании 1.Решение:
а) Нормированная дисперсия ошибки фильтрации ФВ:
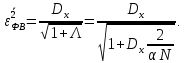
Нормированная дисперсия ошибки фильтрации КФВ:
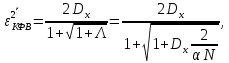
где
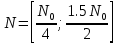 – СПМ шума в заданном диапазоне изменения
– СПМ шума в заданном диапазоне изменения  .
.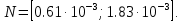
Построим график зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения СПМ шума (рис. 3.1).

11

Рис. 3.1. График зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения СПМ шума
б) Нормированная дисперсия ошибки фильтрации ФВ:
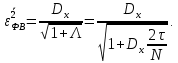
Нормированная дисперсия ошибки фильтрации КФВ:
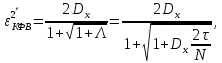
где
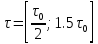 – интервал корреляции сигнала в заданном диапазоне изменения
– интервал корреляции сигнала в заданном диапазоне изменения  .
.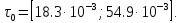
Построим график зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения интервала корреляции сигнала (рис. 3.2).

12

Рис. 3.2. График зависимости нормированных дисперсий ошибок фильтраций ФВ и КФВ от изменения интервала корреляции
Задание 3:
Рассчитать объём выборки (количество
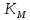 независимых реализаций), при которой относительная ошибка измерения в эксперименте величины
независимых реализаций), при которой относительная ошибка измерения в эксперименте величины  не превысит 1%. При этом приближённо принять интервал корреляции
не превысит 1%. При этом приближённо принять интервал корреляции 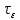 текущей ошибки фильтрации
текущей ошибки фильтрации 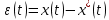 равным удвоенному интервалу корреляции
равным удвоенному интервалу корреляции 
процесса
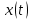 , а отсчёты, отстоящие на интервал корреляции – независимыми.
, а отсчёты, отстоящие на интервал корреляции – независимыми. Решение:
Интервал дискретизации:

Интервал корреляции, согласно заданию, определяется как:
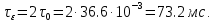

13
Длина реализации, при котором относительная ошибка измерения в эксперименте величины
 не превысит 1%:
не превысит 1%: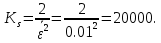
Количество отсчётов
 :
: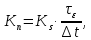
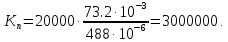
Объём выборки:
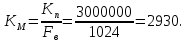
ВЫВОД: из расчётов видно, что лучшие результаты искомых параметров показывает некаузальный фильтр Винера (ФВ), так как он обеспечивает минимум нормированной дисперсии ошибки, по сравнению с квазиоптимальным и каузальным фильтрами. Но фильтр Винера физически нереализуем, что является его существенным недостатком. Это связано с тем, что некаузальный ФВ, использует все входные данные для получения оценки - от ранее поступивших до будущих. Использование прошлых данных, т. е. уже поступивших к текущему моменту времени, физически оправдано и технически реализуемо, а использование будущих данных - невозможно.
Каузальный фильтр Винера, физически реализуем и формирует оценку только за счёт ранее поступивших данных, но имеет ошибку фильтрации значительно выше, чем квазиоптимальный фильтр и фильтр Винера. Это связано с тем, что для образования оценки он использует малое количество данных, в отличие от НКФВ и КОФВ.


14
14
СПИСОК ИСПОЛЬЗОВАННОЙ ЛИТЕРАТУРЫ
-
Применение теории случайных процессов: уч. пособие/ И. С. Грузман. – Новосибирск: Изд-во НГТУ, 2006. – 84 с.; -
Основы случайных процессов: уч. пособие/ И. С. Грузман. – Новосибирск: Изд-во НГТУ, 2004. – 96 с.; -
Лабораторный практикум по курсу “статистическая радиотехника”. Методические указания к лабораторным работам № 1-3 для студентов факультета радиотехники, электроники и физики (специальности 2007) всех форм обучения: уч. пособие/ А. А. Спектор, И. С. Грузман. – Новосибирск: Изд-во НГТУ, 1998. – 33 с.


15
15