Расчетно-графическая работа

по МАТЕМАТИЧЕСКОЙ СТАТИСТИКИ
Вариант 19


Выполнила: ст. группы М-4-2 Щербакова А.Н.

Проверил: Щетинин Е.Ю.

Москва 2002 год

• 
  Условия расчетно-графической работы:
  

Задание 1: По данной выборки построить статистический ряд и эмпирическую функцию распределения. Вычислить выборочное среднее х и оценку дисперсии S². Построить график эмпирической функции распределения.

2,0

3,0

1,0

1,0

5,0

7,0

3,0

4,0

5,0

9,0

Задание 2: Дана выборка из нормально распределенной генеральной совокупности. Найти доверительные интервалы для среднего квадратичного отклонения σ при известном m, или для математического ожидания при известном σ для трех уровней значимости (α₁=0,01 α₂=0,05 α₃=0,1)

Объём выборки 14 m=3,00
1.19	3.34	-.077	1.34	0.99	3.24	1.35	1.40	0.01	1.27	5.58	4.56	1.97	2.61

Задание 3: По заданной выборке (x_i,y_i)(i=1,2,3…10, x_i первая строка y_i вторая строка ) найти оценки методом наименьших квадратов а* b* параметров a и b линейной регрессии Y на X. При этом результаты наблюдений (x_i,y_i) i=1,2,3…10 представляют в виде y_i=b+a*x_i*σ_i, где ошибки наблюдений σ_i независимы и нормально распределены с параметрами (0,1). На координатной плоскости Оху изобразить диаграмму рассеивания и прямую регрессии У на Х.

x	2,04	2,11	0,67	1,93	9,02	7,82	3,03	4,22	9,9	7,97
y	4,37	3,26	4,88	5,11	-4,02	-1,87	0,39	0,37	-4,91	-2,05

---

Задание 4: Партия изделий принимается, если вероятность того, что изделие окажется бракованным, не превышает 0,03. Среди случайно отобранных 400 изделий оказалось 18 бракованных. Можно ли принять партию?
Задание 1

Выборка

2,0

3,0

1,0

1,0

5,0

7,0

3,0

4,0

5,0

9,0

• 
  построение статического ряда
  

в выборке объёмом n элемент x_i встречается n_i раз:

xi	1	2	3	4	5	7	9
yi	2	1	2	1	2	1	1

• 
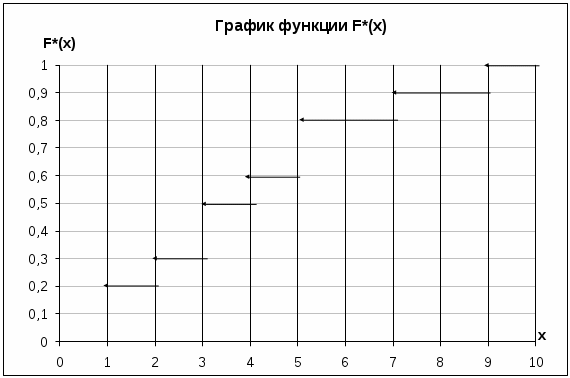
  Построение эмпирической функции распределения
  

Объём выборки: n=2+1+2+1+2+1+1=10

Эмпирической функцией распределения случайной величины Х называется функция F*(x), определяющая для каждого значения х относительную частоту события (Х

F*(x)=m/n

где m-число выборочных значений меньших х (х_i

Наименьшая варианта равна 1 следовательно F*(x)=0 при x<=1

Значение X<2 то есть x=1 наблюдалось 2 раза следовательно F*(x)=2/10=0,2 при 1
Значение X<3 то есть x=1 и х=2 наблюдалось 2+1=3 раза следовательно F*(x)=3/10=0,3 при 2
Значение X<4 наблюдалось 5 раз следовательно F*(x)=0,5 при 3
Значение X<5 наблюдалось 6 раз следовательно F*(x)=0,6 при 4
Значение X<7 наблюдалось 8 раз следовательно F*(x)=0,8 при 5
Значение X<9 наблюдалось 9 раз следовательно F*(x)=0,9 при 7
Значение X>9 наблюдалось 10 раз следовательно F*(x)=1 при x>9

Э
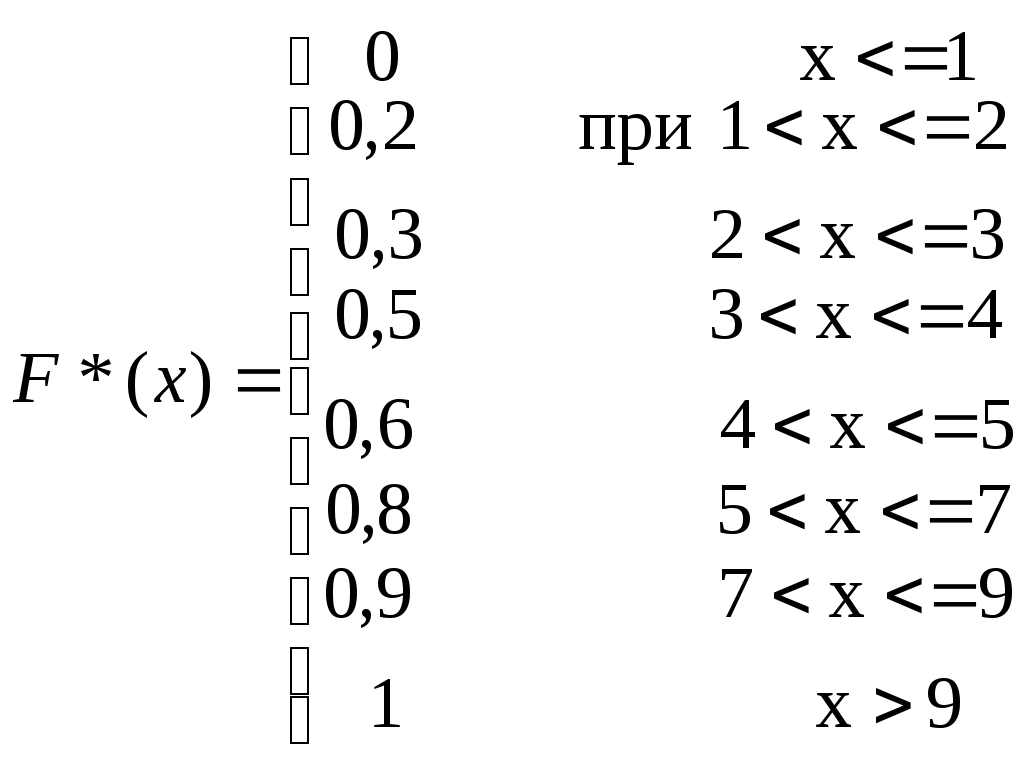
мпирическая функция имеет вид:

Выборочное среднее- называется среднее арифметическое элементов выборки

И
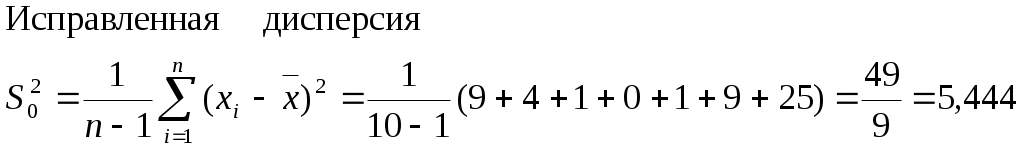
справленная дисперсия (выборочная)-среднее арифметическое квадратов отклонений наблюдаемых значений выборки от выборочного среднего







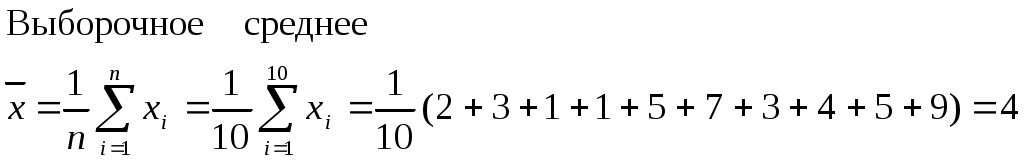
Задание 2

Объём выборки 14 m=3,00
1.19	3.34	-.077	1.34	0.99	3.24	1.35	1.40	0.01	1.27	5.58	4.56	1.97	2.61

• 
  
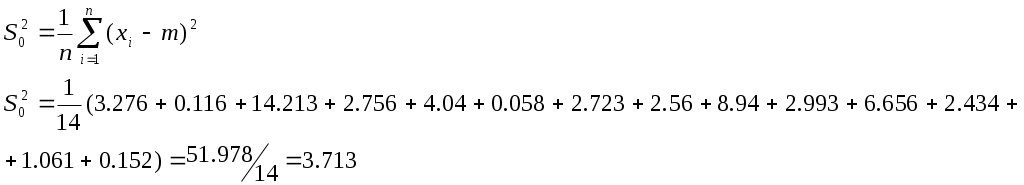
  Оценка дисперсии
  

Где n-объем выборки x_i i-й элемент выборки m-математическое ожидание

α-уровень значимости

• 
  при α=0,01
  

П
о таблице значений квантилей распределения хи-квадрат находим:

где: Х_α/2²(n)-квантиль порядка α/2 распределения хи-квадрат

Х_1-α/2²(n)-квантиль порядка 1-α/2 распределения хи-квадрат

• 
  
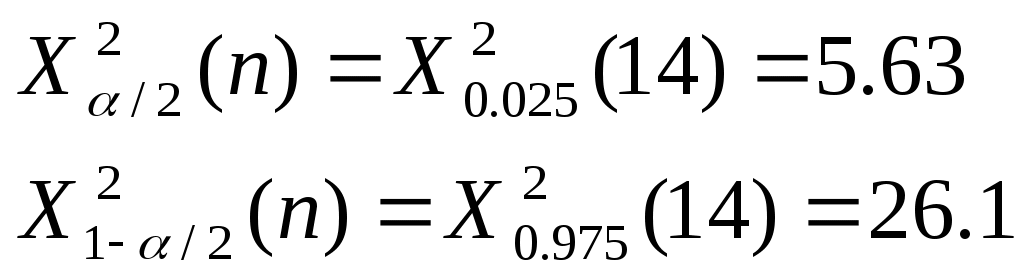
  при α=0,05
  

По таблице находим:

• 
  при α=0,1
  

П
о таблице находим:

• 
  д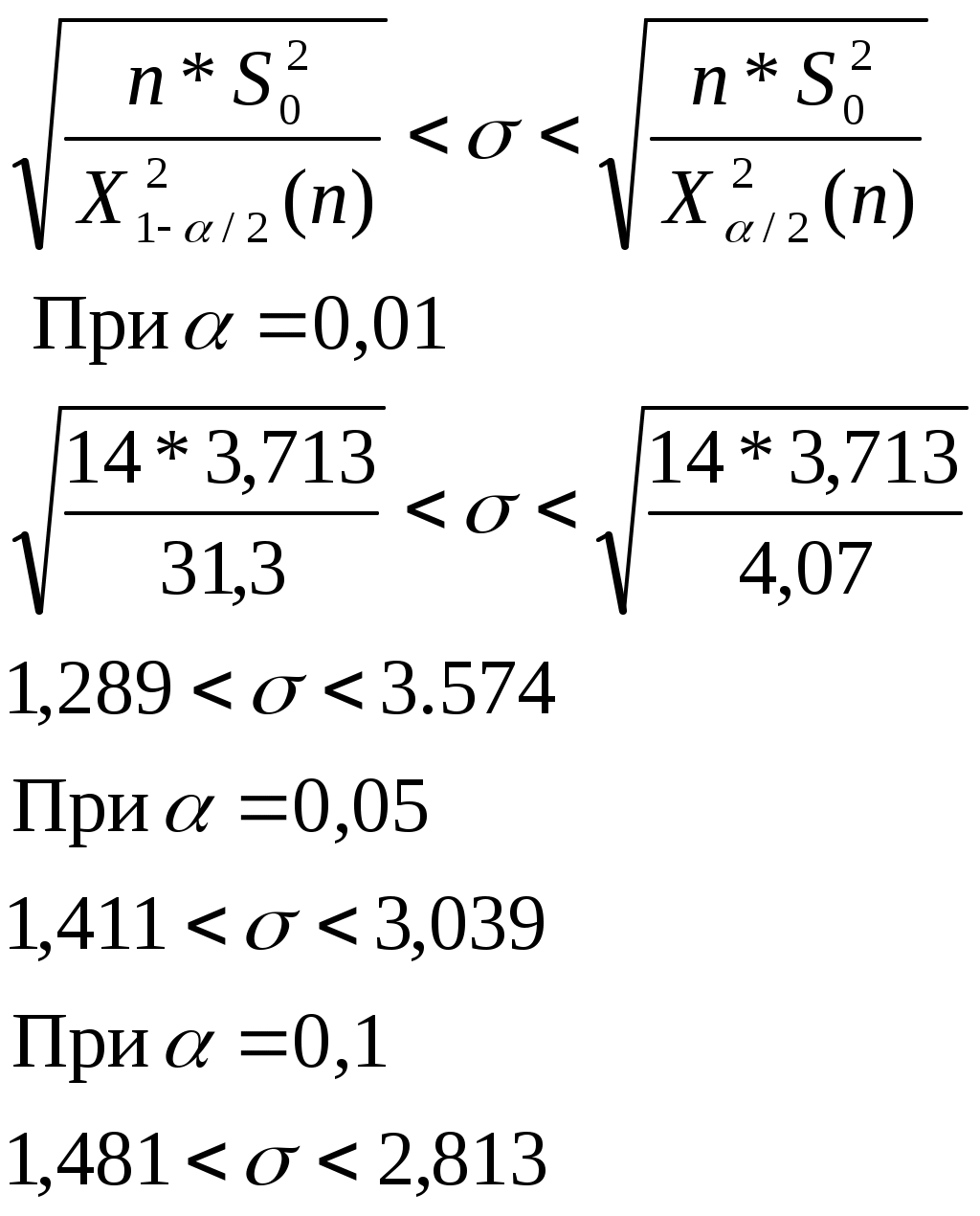
  оверительный интервал для среднего квадратичного отклонение
  

Задание 3

x	2,04	2,11	0,67	1,93	9,02	7,82	3,03	4,22	9,9	7,97
y	4,37	3,26	4,88	5,11	-4,02	-1,87	0,39	0,37	-4,91	-2,05

Диаграмма рассеивания-предварительное представление о зависимости между Х и Y можно получить, нанося элементы выборки (хi;yi), i=1,2,…k в виде точек на плоскости с выбранной системой координат.

y_i=b*+a*x_i+δ_i

• 
  О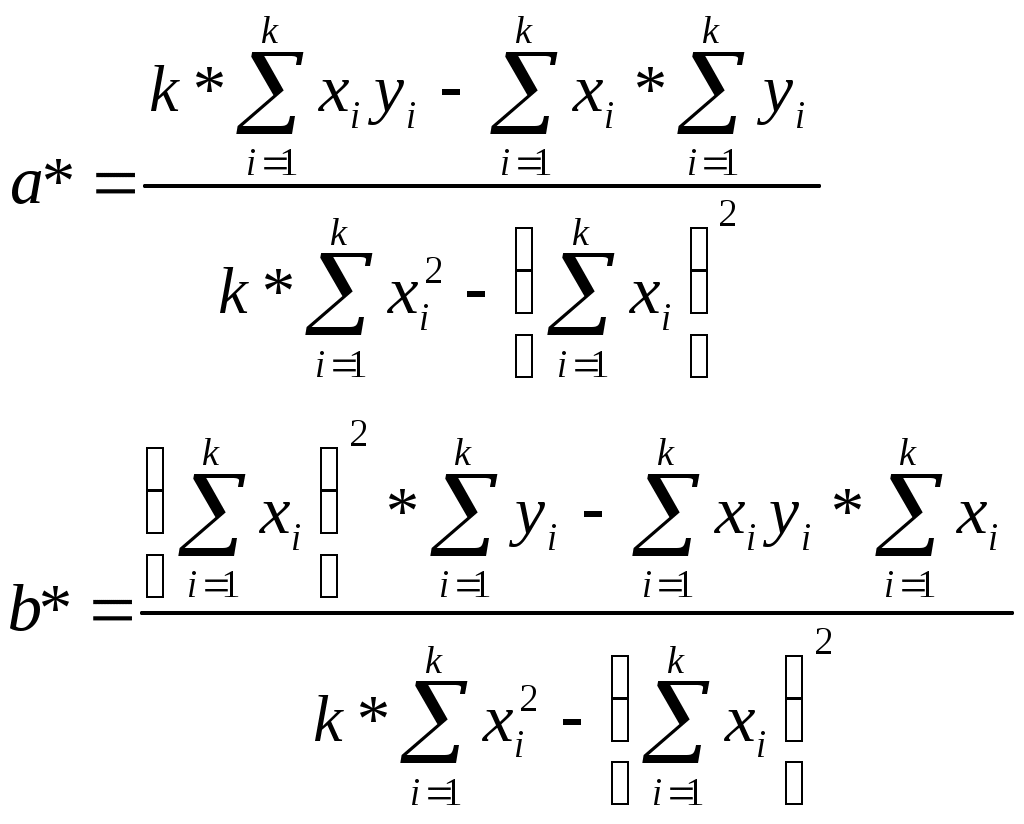
  ценка параметров а* и в* по методу наименьших квадратов:
  

значения											сумма
xi	2,04	2,11	0,67	1,93	9,02	7,82	3,03	4,22	9,9	7,97	48,71
yi	4,37	3,26	4,88	5,11	-4,02	-1,87	0,39	0,37	-4,91	-2,05	5,53
xi2	4,16	4,45	0,45	3,72	81,36	61,15	9,18	17,81	98,01	63,52	343,82
xiyi	8,91	6,88	3,27	9,86	-36,26	-14,62	1,18	1,56	-48,61	-16,34	-84,16

Таким образом подставляя значения в формулы получим:

a*=-1,04

в*=5,63

• 
  Искомое уравнение регрессии имеет вид:
  

Y=-1,04x+5,63

Для того чтобы получить представление, насколько хорошо вычисленые по этому уравнению значения У_i согласуются с наблюдаемыми значениями y_i, найдем отклонения Y_i-y_i

• 
  Отклонение Y_i-y_i:
  

xi	2,04	2,11	0,67	1,93	9,02	7,82	3,03	4,22	9,9	7,97
yi	4,37	3,26	4,88	5,11	-4,02	-1,87	0,39	0,37	-4,91	-2,05
Yi	3,50	3,43	4,93	3,62	-3,77	-2,52	2,47	1,23	-4,69	-2,68
Yi-yi	-0,87	0,17	0,05	-1,49	0,25	-0,65	2,08	0,86	0,22	-0,63

• 
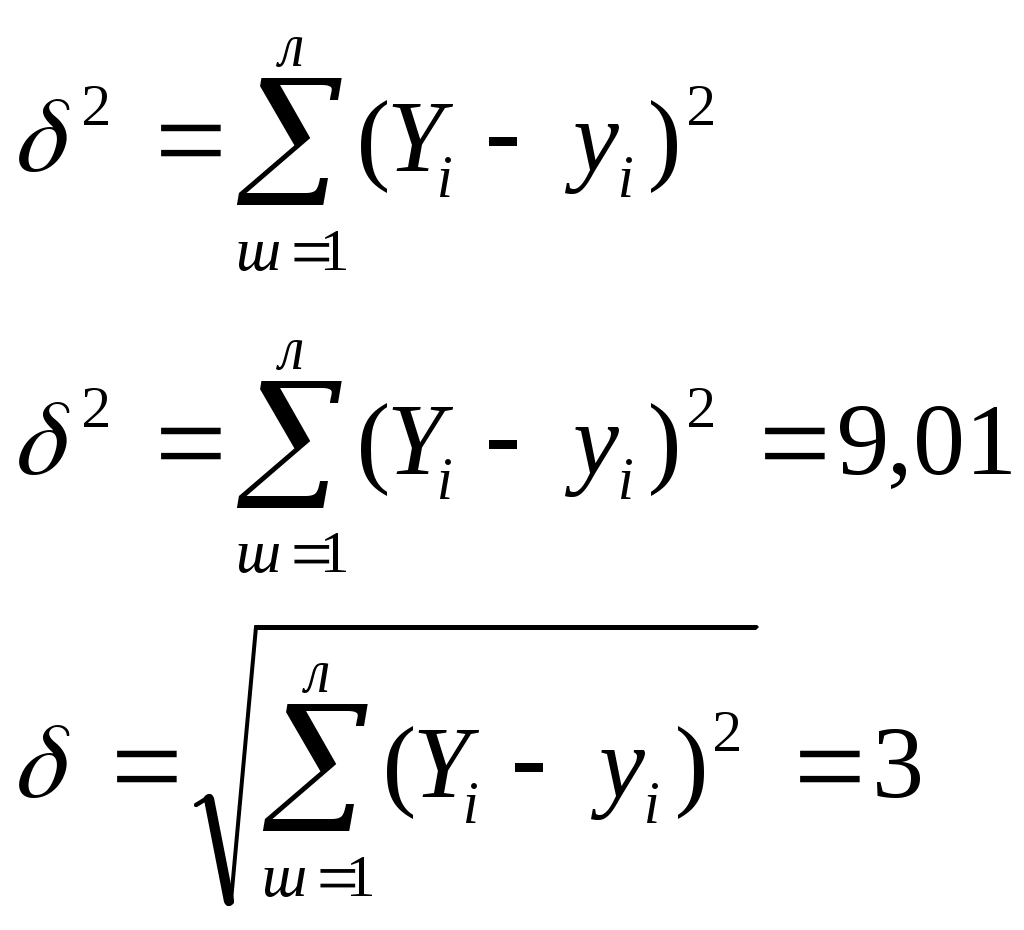
  Ошибка наблюдений δ
  

• 
  Д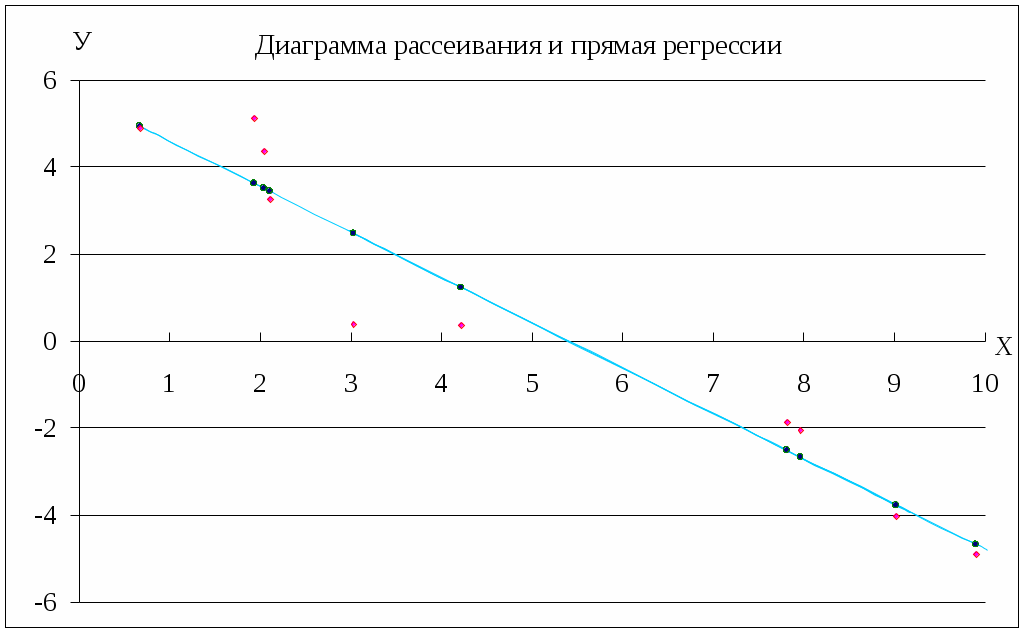
  иаграмма рассеивания и прямая регрессии:
  

Задание №4

H₀- партия не принята (нулевая гипотеза- выдвинутая гипотеза, которую нужно проверить)

H₁-партия принята (альтернативная гипотеза)

H₀: p=p₀

H₁: p≠p₀

Так как n*p_o*q_o=n*p_o*(1-p_o)=400*0,03*(1-0,03)=11,64 >9, для проверки гипотезы H₀ можно использовати статистику
П
усть Х- случайная величина, равная числу успехов в n испытаниях, и пусть вероятность успеха в каждом испытании равна р, тогда величина Х имеет биноминальное распределение с параметрами n и p:

Т
ребуется при заданном уровне значимости α=0,03 проверить нулевую гипотезу, состоящую в том, что неизвестная вероятность р равна гипотической вероятности р_о. Для проверки нулевой гипотезы используют статистику:

В данной задаче число испытаний n=400 число исходов опыта благоприятных появлению бракованных изделий равна х=18

h=x/n=18/400

q_o=(1-p_o)=0,97

В
ычислим значение статистики:

По таблице квантилей стандартного нормального распределения определяем:

Т
ак как U>u_1-α/2- есть основание отвергнуть нулевую гипотезу H₀- партия не принята, следовательно верна альтернативная гипотеза, т.е. H₁-партия принята.
Ответ: партия принята

9>7>5>4>3>2>

---

Смотрите также файлы

• Результат практики.docx

• Абонементная плата.docx

• Попытки ввести лекарство в организм человека прямо в кровь, минуя пищеварительный тракт, делались с тех самых пор, как человек получил элементарное представление об анатомии.docx

• Этапы многолетней спортивной подготовки.docx

• Оформление документа.doc