ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 36
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
(37)
Подставляем числа (переводя одновременно все величины в СИ).
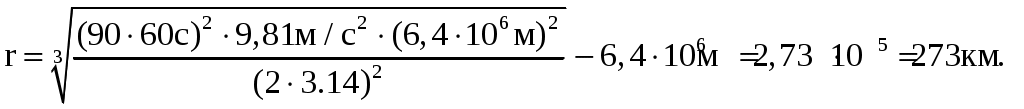
Ответ: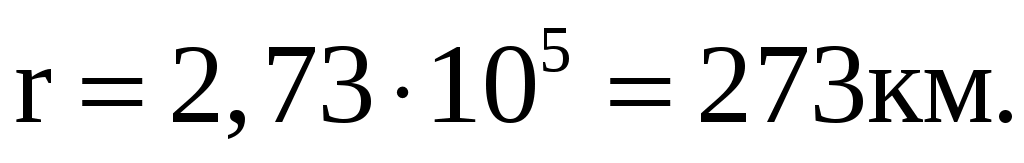
1.75 Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.
Дано: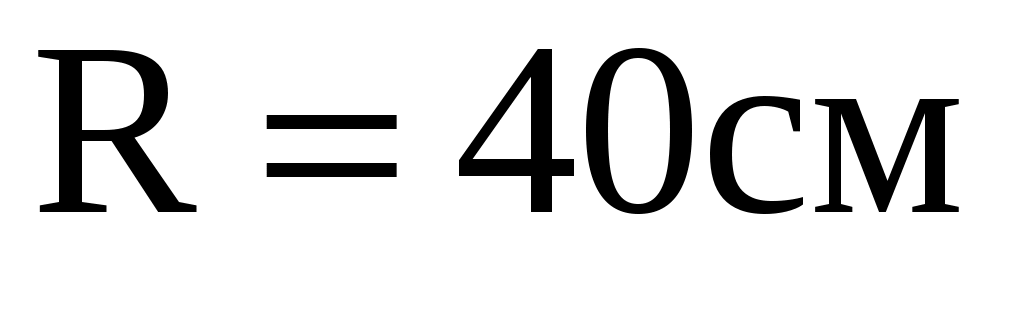
Найти: T=?
Решение:

Известно, что период колебаний физического маятника (ф.м. – это твердое тело, совершающее колебания под действием силы тяжести относительно горизонтальной оси) равно
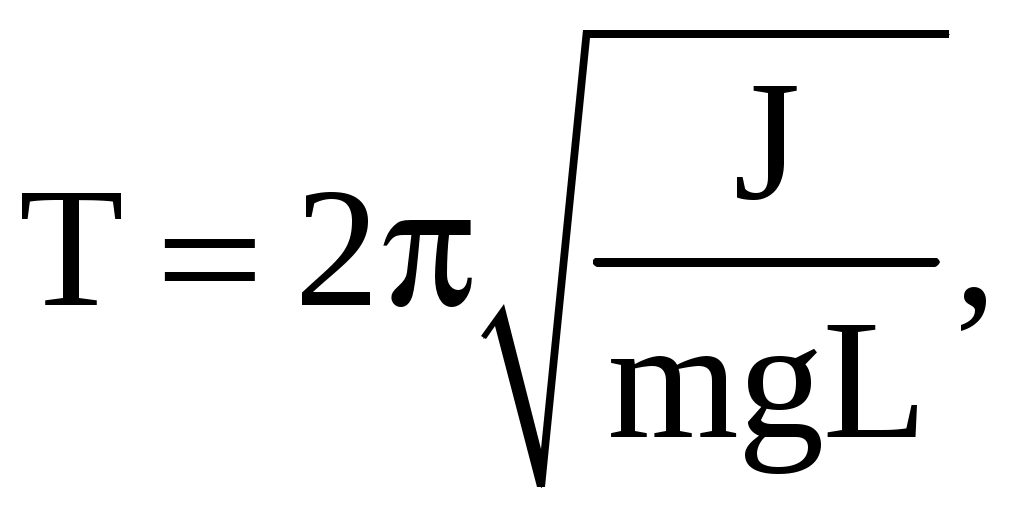 (38)
(38)
где J – момент инерции тела относительно точки подвеса;
m – масса физического маятника;
L – расстояние от точки подвеса до центра тяжести тела (в нашем случае L=AO=R).
Для нашего случая нужно найти момент инерции диска J относительно точки подвеса А. Для того чтобы вычислить J воспользуемся теоремой Штейнера:
Если ось вращения тела параллельна оси симметрии, но смещена от нее на расстояние х, то момент инерции J относительно параллельно смещенной оси выражается соотношением
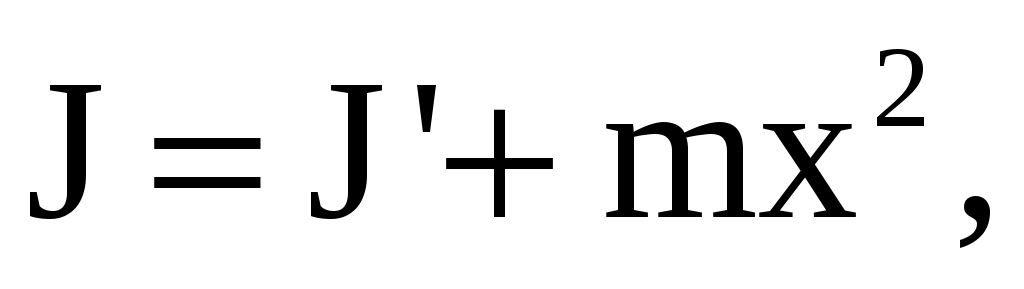 (39)
(39)
где - момент инерции тела относительно его оси симметрии. В нашем случае
- момент инерции тела относительно его оси симметрии. В нашем случае
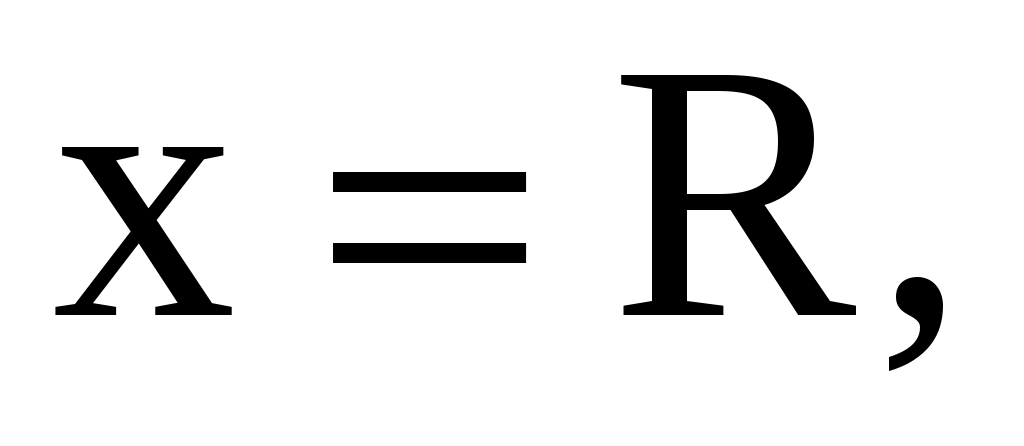 (40)
(40)
a
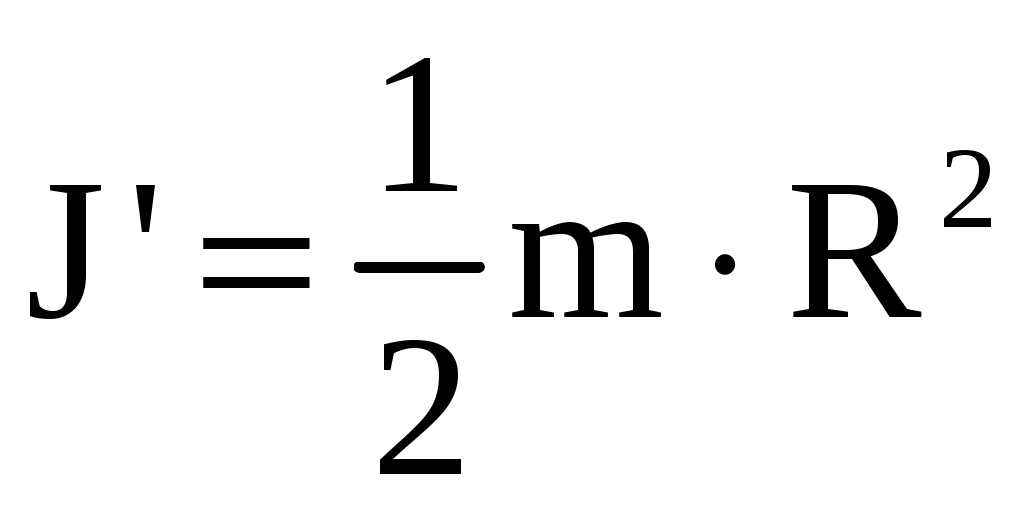 - момент инерции диска относительно его оси симметрии,
- момент инерции диска относительно его оси симметрии,
поэтому
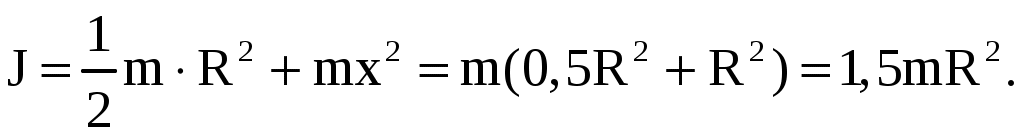 (41)
(41)
Тогда
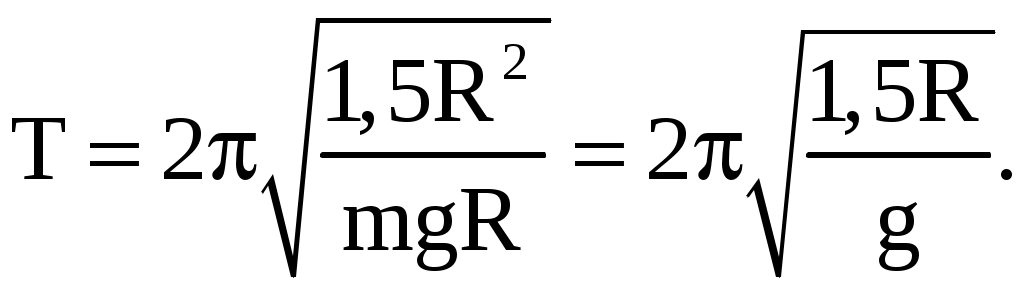 (42)
(42)
Подставляем числа (переводя одновременно все виличины в систему СИ).
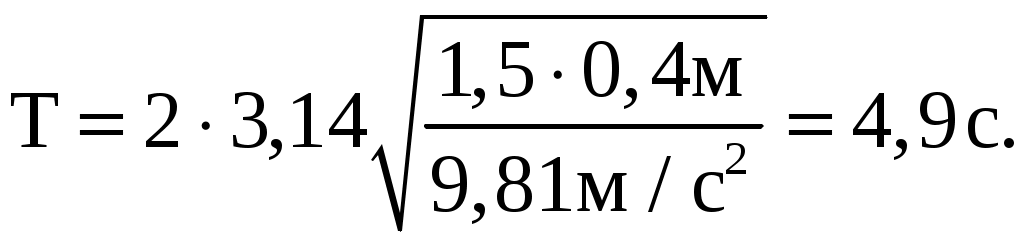
Ответ: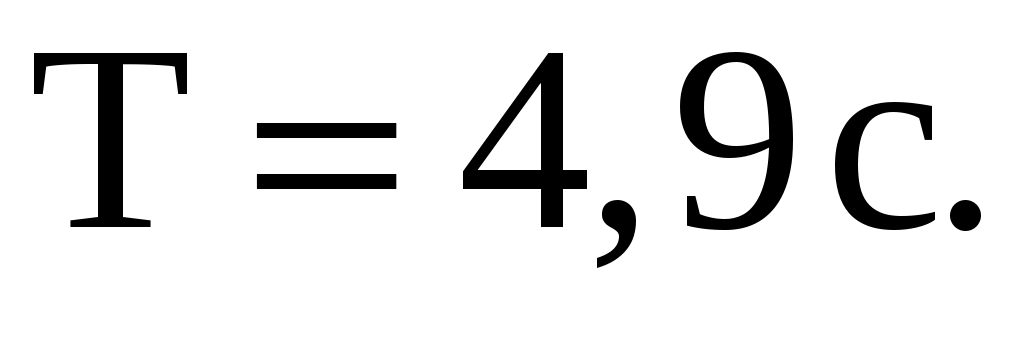
Подставляем числа (переводя одновременно все величины в СИ).
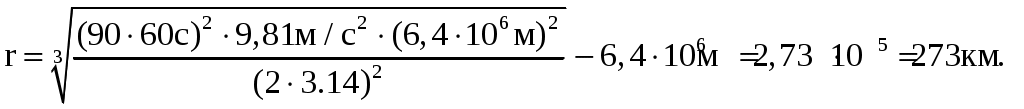
Ответ:
1.75 Определить период Т простых гармонических колебаний диска радиусом R = 40 см около горизонтальной оси, проходящей через образующую диска.
Дано:
Найти: T=?
Решение:

Известно, что период колебаний физического маятника (ф.м. – это твердое тело, совершающее колебания под действием силы тяжести относительно горизонтальной оси) равно
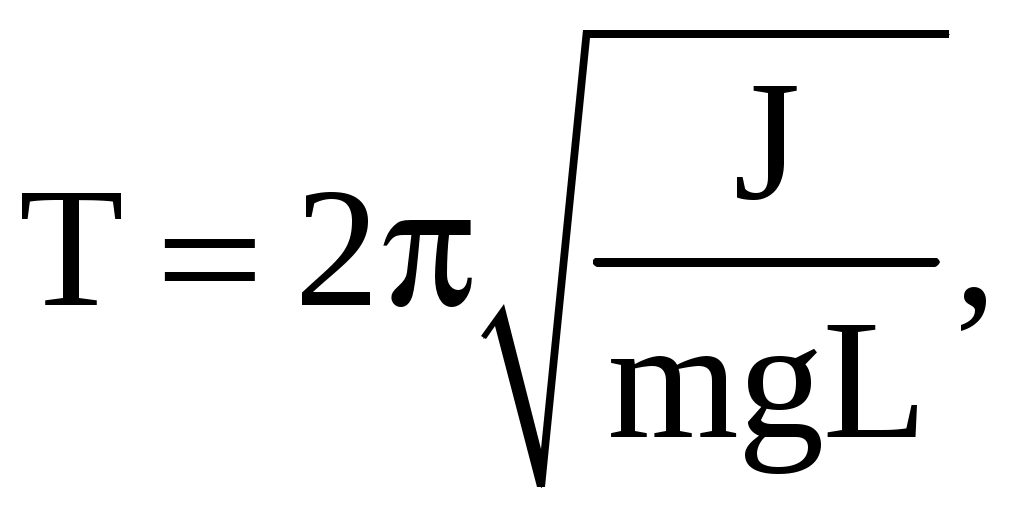 (38)
(38)где J – момент инерции тела относительно точки подвеса;
m – масса физического маятника;
L – расстояние от точки подвеса до центра тяжести тела (в нашем случае L=AO=R).
Для нашего случая нужно найти момент инерции диска J относительно точки подвеса А. Для того чтобы вычислить J воспользуемся теоремой Штейнера:
Если ось вращения тела параллельна оси симметрии, но смещена от нее на расстояние х, то момент инерции J относительно параллельно смещенной оси выражается соотношением
где
a
поэтому
Тогда
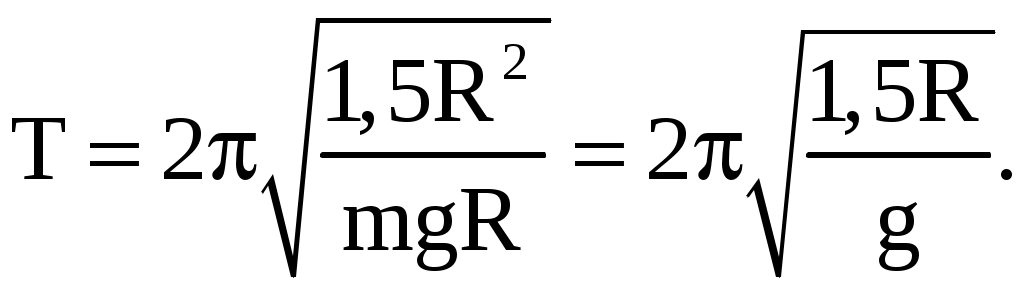 (42)
(42)Подставляем числа (переводя одновременно все виличины в систему СИ).
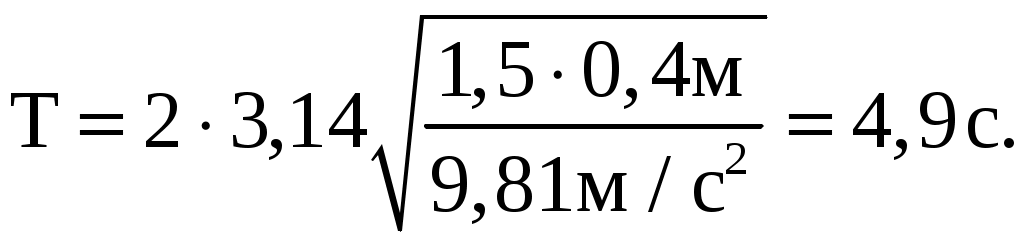
Ответ: