Файл: Вычисление определенного интеграла Екатеринбург 2006 Вычисление определенного интеграла.rtf
Добавлен: 03.12.2023
Просмотров: 34
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
абсолютная ошибка результата, полученного по формуле Симпсона, меньше 0,00011. Это находится в соответствии с данной выше оценкой погрешности и, кроме того, свидетельствует, что формула Симпсона значительно точнее формулы трапеций. Поэтому формулу Симпсона для приближенного вычисления определенных интегралов используют чаще, чем формулу трапеций.
Сравним методы по точности, для этого произведем вычисления интеграла функций y=x, y=x+2, y=x2, при n=10 и n=60, a=0, b=10. Точное значение интегралов составляет соответственно: 50, 70, 333.(3)
таблица 1
Из таблицы 1 видно, что наиболее точным является интеграл, найденный по формуле Симпсона, при вычислении линейных функций y=x, y=x+2 также достигается точность методами средних прямоугольников и методом трапеций, метод правых прямоугольников является менее точным. Из таблицы 1 видно, что при увеличении количества разбиений n (увеличения числа интеграций) повышается точность приближенного вычисления интегралов
f(x)=x2
f(x)= x3
f(x)= x4
на отрезке [0, 1] с шагом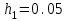 ,
, 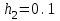 ,
, 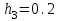
f(x)=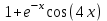
f(x)=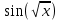
Таблица 2 Индивидуальные варианты задания
Вычисление определенного интеграла: Методические указания к лабораторной работе по дисциплине «Вычислительная математика» / сост. И.А.Селиванова. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 14 с.
Указания предназначены для студентов всех форм обучения специальности 230101 – «Вычислительные машины, комплексы, системы и сети» и бакалавров направления 230100 – «Информатика и вычислительная техника». Составитель Селиванова Ирина Анатольевна
Сравнение методов по точности
Сравним методы по точности, для этого произведем вычисления интеграла функций y=x, y=x+2, y=x2, при n=10 и n=60, a=0, b=10. Точное значение интегралов составляет соответственно: 50, 70, 333.(3)
таблица 1
| метод | n | x | x+2 | x2 |
| Метод средних прямоугольников | 10 | 50 | 70 | 332.5 |
| Метод правых прямоугольников | 10 | 45 | 65 | 285 |
| Метод трапеции | 10 | 50 | 70 | 335 |
| Формула Симпсона | 10 | 50 | 70 | 333.333 |
| | | | | |
| Метод средних прямоугольников | 60 | 50 | 70 | 333.310 |
| Метод правых прямоугольников | 60 | 49.1667 | 69.1667 | 325.046 |
| Метод трапеции | 60 | 50 | 70 | 333.379 |
| Формула Симпсона | 60 | 50 | 70 | 333.333 |
Из таблицы 1 видно, что наиболее точным является интеграл, найденный по формуле Симпсона, при вычислении линейных функций y=x, y=x+2 также достигается точность методами средних прямоугольников и методом трапеций, метод правых прямоугольников является менее точным. Из таблицы 1 видно, что при увеличении количества разбиений n (увеличения числа интеграций) повышается точность приближенного вычисления интегралов
Задание на лабораторную работу
-
Написать программы вычисления определенного интеграла методами: средних, правых прямоугольников, трапеции и методом Симпсона. Выполнить интегрирование следующих функций:
-
f(x)=x
f(x)=x2
f(x)= x3
f(x)= x4
на отрезке [0, 1] с шагом
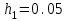 ,
, 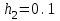 ,
, 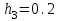
-
f(x)=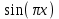
f(x)=
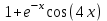
f(x)=
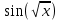
-
Выполнить вариант индивидуального задания (таблица 2)
Таблица 2 Индивидуальные варианты задания
| № | Функция f(x) | Отрезок интегрирования [a,b] |
| 1 | | [1;3] |
| 2 | | [1;3] |
| 3 | | [0;2] |
| 4 | | [2;4] |
| 5 | | [1;3] |
| 6 |  | [0;2] |
| 7 | | [0;2] |
| 8 | | [1;3] |
| 9 | | [0;2] |
| 10 | | [0;2] |
| 11 | | [1;3] |
| 12 | | [1;3] |
| 13 | | [0;2] |
| 14 | | [2;4] |
| 15 | | [1;3] |
| 16 |  | [0;2] |
| 17 | | [0;2] |
| 18 | | [1;3] |
| 19 | | [0;2] |
| 20 | | [0;2] |
| 21 | | [1;3] |
| 22 | | [1;3] |
| 23 | | [0;2] |
| 24 | | [2;4] |
| 25 | | [1;3] |
| 26 |  | [0;2] |
| 27 | | [0;2] |
| 28 | | [1;3] |
| 29 | | [0;2] |
| 30 | | [0;2] |
-
Провести сравнительный анализ методов.
Вычисление определенного интеграла: Методические указания к лабораторной работе по дисциплине «Вычислительная математика» / сост. И.А.Селиванова. Екатеринбург: ГОУ ВПО УГТУ-УПИ, 2006. 14 с.
Указания предназначены для студентов всех форм обучения специальности 230101 – «Вычислительные машины, комплексы, системы и сети» и бакалавров направления 230100 – «Информатика и вычислительная техника». Составитель Селиванова Ирина Анатольевна