Файл: Отчет по лабораторной работе 2 по дисциплине Информатика.docx
Добавлен: 03.12.2023
Просмотров: 38
Скачиваний: 2
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ
РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное бюджетное образовательное учреждение высшего образования
«Воронежский государственный технический университет»
(ФГБОУ ВО «ВГТУ», ВГТУ)
Факультет информационных технологий и компьютерной безопасности
Кафедра систем управления и информационных технологий в строительстве
Отчет по лабораторной работе 2
по дисциплине: «Информатика»
Выполнил студент: Хрячков Н.В.
Группа: бИСТ-222
Руководитель: доцент, к.т.н. Ефимова О.Е.
Работа защищена « » 2023г.
С
(подпись)
оценкой
Воронеж 2023
Лабораторная работа № 1
«Метод последовательных приближений (метод итераций).
Понятие рекуррентной формулы. Ряд Тейлора»
1 Цель работы.
Научиться работать с рядом Тэйлора на языке программирования C++.
-
Задание на лабораторную работу
1. Вычислить и вывести на экран в виде таблицы значения функции за-
данной с помощью ряда Тейлора на интервале от хn до xk с шагом dx.
Реализовать два цикла вычисления значений функции:f1(x) - для вычис-
ления ряда с заданной точностью ε1 = 0.1 и f2(x) - для вычисления ряда с за-
данной точностью ε2 = 0.000001.
Каждая строка таблицы должна содержать значение аргумента, значение
заданной f(x), точность eps1, значение функции f1(x), точность eps2, значение
функции f2(x)
Оценить скорость сходимости ряда, найдя число слагаемых, необходи-
мое для достижения каждой из заданных погрешностей.
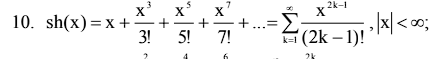
2. Найти
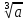как предел последовательности 
,
,
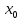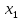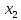,…, где 
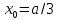в каждое следующее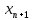 
получается из предыдущего по формуле:
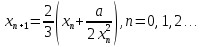
3. Пусть дано натуральное число n. Найдите наименьшее среди чисел
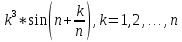
4. Пусть дано натуральное число n. Найдите
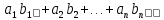, где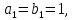 
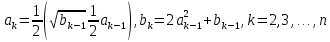
5. Проверить численно замечательные пределы:
a) первый:
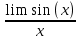, задавая значения 
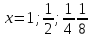до тех пор, пока левая часть равенства не будет отличаться от правой менее, чем на заданнуювеличину погрешности
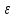.b) второй:
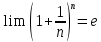задавая значения n = 1;2;3…. При каком n исследуемое выражение будет отличаться от е менее, чем на заданную величину погрешности 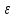.3 Ход выполнения
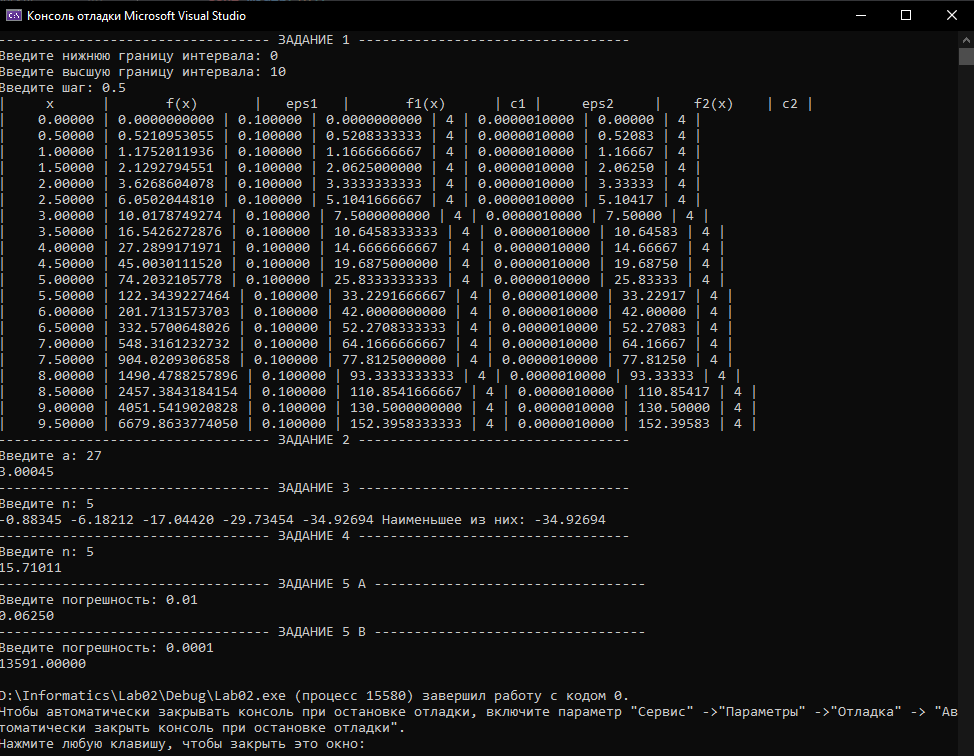
Рисунок 1 – Работа всей программы
4 Вывод
Научился работать с рядом Тэйлора на языке программирования C++.
Приложение А
#include
#include
#define E 2.718
using namespace std;
struct FRES {
double sum;
int counter;
};
int f(double x, double eps, FRES * conf);
double f2(double x, double eps);
double f3(int n);
double fact(int n);
double f4(int n);
double func5a(double eps);
double func5b(double eps);
int main()
{
setlocale(LC_ALL, "RUS");
cout << "---------------------------------- ЗАДАНИЕ 1 ----------------------------------" << endl;
double mx, dx, step;
cout << "Введите нижнюю границу интервала: ";
cin >> mx;
cout << "Введите высшую границу интервала: ";
cin >> dx;
cout << "Введите шаг: ";
cin >> step;
cout << "| x | f(x) | eps1 | f1(x) | c1 | eps2 | f2(x) | c2 |" << endl;
for (double i = mx; i < dx; i += step) {
FRES conf1;
FRES conf2;
FRES* res1 = &conf1;
FRES* res2 = &conf2;
f(i, 0.1, res1);
f(i, 0.000001, res2);
cout << fixed << "| ";
cout.precision(5);
cout.width(10);
cout << i << " | ";
cout.precision(10);
cout.width(10);
cout << sinh(i) << " | ";
cout.precision(6);
cout << 0.1 << " | ";
cout.precision(10);
cout.width(10);
cout << res1->sum << " | ";
cout << fixed << res1->counter << " | ";
cout << 0.000001 << " | ";
cout.precision(5);
cout.width(5);
cout << res2->sum << " | ";
cout << res2->counter << " | " << endl;
}
double a;
cout << "---------------------------------- ЗАДАНИЕ 2 ----------------------------------" << endl;
cout << "Введите a: ";
cin >> a;
cout << f2(a, 0.1) << endl;
double n;
cout << "---------------------------------- ЗАДАНИЕ 3 ----------------------------------" << endl;
cout << "Введите n: ";
cin >> n;
cout << "Наименьшее из них: " << f3(n) << endl;
cout << "---------------------------------- ЗАДАНИЕ 4 ----------------------------------" << endl;
cout << "Введите n: ";
cin >> n;
cout << f4(n) << endl;
cout << "---------------------------------- ЗАДАНИЕ 5 A ----------------------------------" << endl;
double eps;
cout << "Введите погрешность: ";
cin >> eps;
cout << func5a(eps) << endl;
cout << "---------------------------------- ЗАДАНИЕ 5 B ----------------------------------" << endl;
cout << "Введите погрешность: ";
cin >> eps;
cout << func5b(eps) << endl;
}
int f(double x, double eps, FRES * conf) {
int n = 3;
double prev = x;
double next = (pow(x, 3) / fact(3));
double sum = prev + next;
double R = next / prev;
double un = next;
while (fabs(next - sum) <= eps) {
sum -= un;
break;
}
next = sum;
n++;
conf->counter = n;
conf->sum = sum;
return 1;
}
double f2(double x, double eps) {
double prevValue = x / 3;
double nextValue = (2. / 3.) * (prevValue + (x / (2 * pow(prevValue, 2))));
double sum = prevValue + nextValue;
while (fabs(nextValue - prevValue) > eps) {
prevValue = nextValue;
nextValue = 2.0 * (prevValue + x / (2 * prevValue * prevValue)) / 3.0;
}
return nextValue;
}
double f3(int n) {
double min = 10000000;
for (int k = 1; k <= n; k++) {
double number = pow(k, 3) * sin(n + k / double(n));
cout << number << " ";
if (number < min) {
min = number;
}
}
return min;
}
double f4(int n) {
double sum = 0;
double a, b, aPrev, bPrev;
a = 1;
b = 1;
sum = a * b;
for (int i = 2; i < n; i++) {
aPrev = a;
bPrev = b;
a = (1.0 * (sqrt(bPrev) + 0.5 * aPrev)) / 2.0;
b = 2 * pow(aPrev, 2) + bPrev;
sum += a * b;
}
return sum;
}
double func5a(double eps) {
double val = 0;
double x = 1;
double preRes = sin(x) / x;
x /= 2;
val = sin(x) / x;
x /= 2;
while (fabs(val - preRes) > eps) {
preRes = val;
val = sin(x) / x;
x /= 2;
}
return x;
}
double func5b(double eps) {
double k = 0;
int n = 1;
while (fabs(k - exp(1.0)) > eps)
{
n++;
k = pow((1 + 1.0 / n), n);
}
return n;
}
double fact(int n) {
double res = 1;
for (int i = 1; i <= n; i++) {
res *= i;
}
return res;
}