Добавлен: 03.12.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
=-1 и 
=1) положить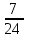 
, то получим 
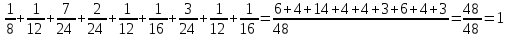.Все дальнейшие расчеты будем производить для совместного распределения (иначе не получим ряды распределения) при
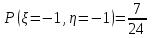
Таблица 2.
| \ | -1 | 0 | 1 |
| -1 | 1/8 | 1/12 | 7/24 |
| 0 | 2/24 | 1/12 | 1/16 |
| 1 | 3/24 | 1/12 | 1/16 |
Для того, что бы найти безусловный закон распределения
выполним сложение вероятностей по столбцам.Таблица3.
| | -1 | 0 | 1 |
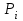 | 1/8+2/24+3/24=1/3 | 3/12=1/4 | 7/24+2/16=5/12 |
Для того, что бы найти безусловный распределения
выполним сложение вероятностей по строкам.Таблица 4.
| | -1 | 0 | 1 |
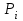| | 1/8+1/12+7/24=1/2 | 2/24+1/12+1/16=11/48 | 3/24+1/12+1/16=13/48 |
Вычислим математические ожидания
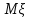и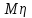 
.
,
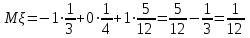
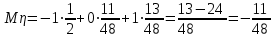.Центр распределения:
, 
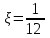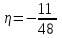.Б) найдем условный закон распределения
при 
.В таблице 3 найдено
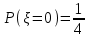.Условный закон распределения случайной величины
при условии, что , найдем применяя формулу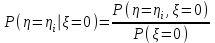 
тогда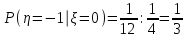 
, 
, 
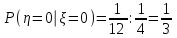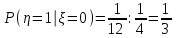
То есть
Таблица 5.
| / | -1 | 0 | 1 |
 | 1/3 | 1/3 | 1/3 |
В) Найдем условное математическое ожидание
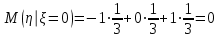.г) Найдем закон распределения СВ
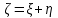.Вычислим все возможные суммы и запишем их вероятности
, 
, 
, 
, 
, 
,
, 
, 
,
,
, 
, 
, 
, 
, 
, 
, 
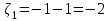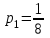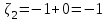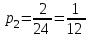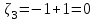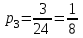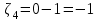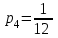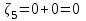
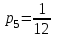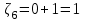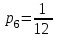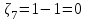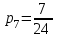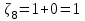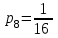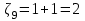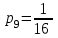, Объединим одинаковые значения и вычислим
, 
, 
, 
, 
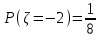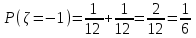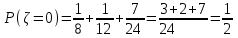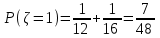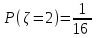
Таблица 6.
 | -2 | -1 | 0 | 1 | 2 |
| | 1/8 | 1/6 | 1/2 | 1/2 | 1/16 |
Ответ: заданное распределение не является законом распределения, рассматриваем распределение из таблицы 2.
а) таблица3, таблица 4, центр
, 
.б) таблица 5, в)
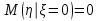, г) таблица 6.5. Задан статистический ряд
Таблица 7.
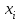 | 9-10 | 10-11 | 11-12 | 12-13 | 13-14 |
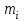 | 18 | 52 | 48 | 34 | 28 |
а) Построить гистограмму. Найти
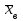
, моду, медиану и
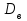.б) Оценить доверительный интервал для
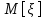с надежностью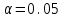 
Решение.
а) Построим гистограмму частот заданного ряда распределения, отметив на оси абсцисс – интервалы распределения, а на оси ординат их частоты и построим прямоугольники.
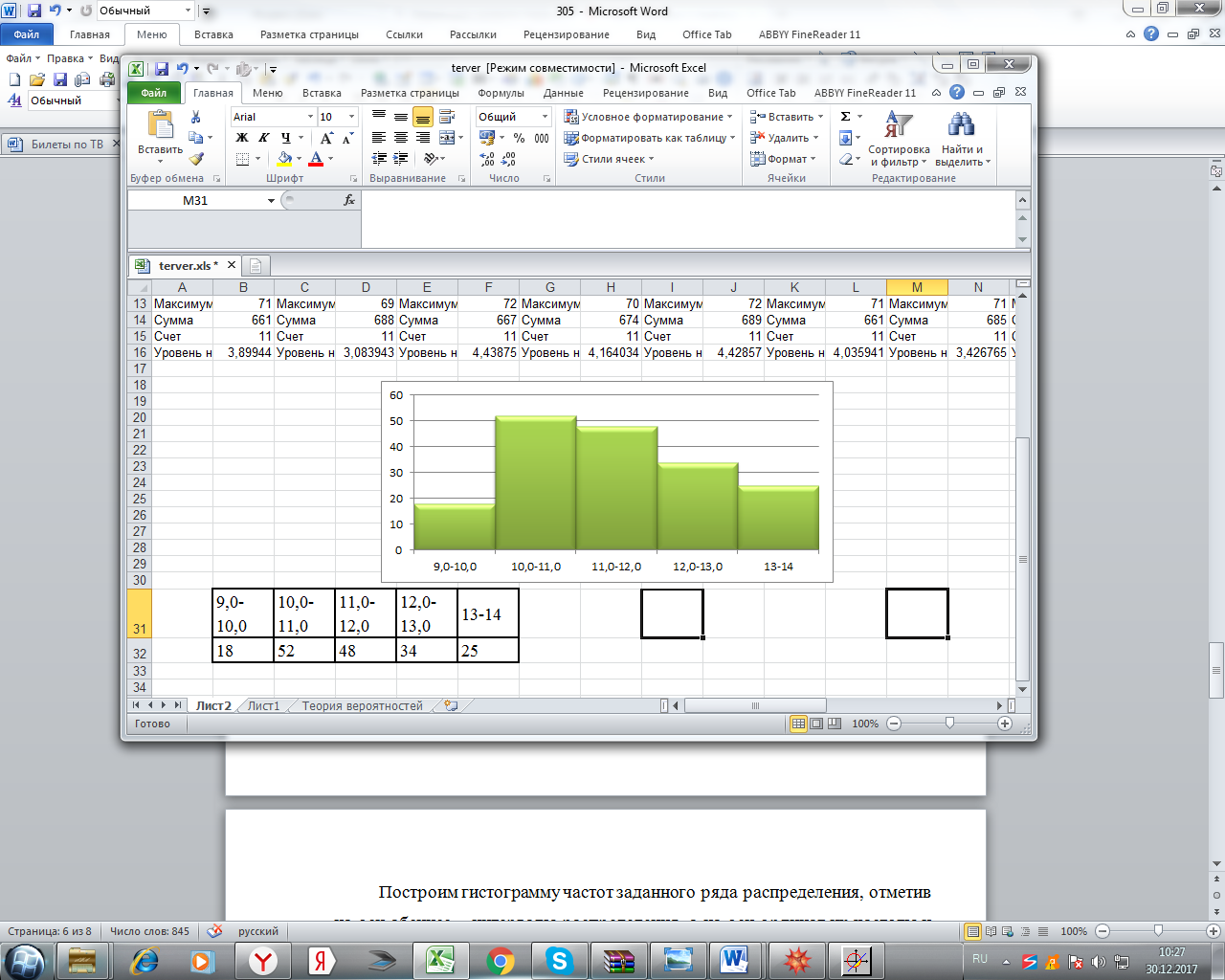
Рис.2.
Для вычисления числовых характеристик перейдем от интервального ряда к вариационному, взяв в качестве вариант середины интервалов.
Выборочный ряд распределения имеет вид.
Таблица 8.
 | 9,5 | 10,5 | 11,5 | 12,5 | 13,5 |
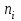 | 18 | 52 | 48 | 34 | 28 |
Объем выборки
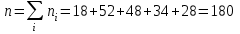.Выборочное среднее
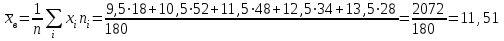.Выборочная дисперсия
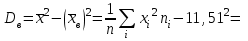
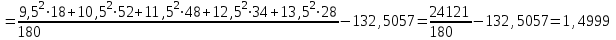Для дискретного ряда вычислим моду и медиану Мода – это значение, которое встречается в выборке наиболее часто, тогда мода
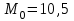.Медиана – это значение варианты, которое делит ранжированный ряд на две равные по численности совокупности (в нашем случае – это полусумма вариант, которые находятся на 89 и 90 месте) , 18+52=70, 70++48=118, тогда
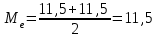.Для интервального ряда вычислим моду и медиану.
В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул:
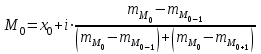, где
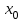
– нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту);
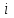– величина модального интервала; 
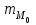– частота модального интервала; 
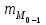– частота интервала, предшествующего модальному; 
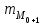– частота интервала, следующего за модальным. Тогда
, 
, 
, 
, 
.
.
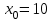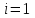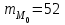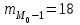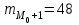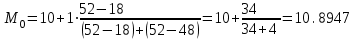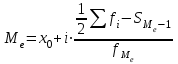
где
– нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); 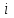– величина медианного интервала; 
– накопленная частота интервала, предшествующего медианному;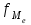 
– частота медианного интервала. 
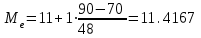.б) Доверительный интервал, покрывающий неизвестное математическое ожидание
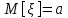с вероятностью 
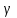имеет вид: 
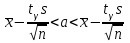, где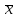 
- среднее генеральной совокупности,