Файл: Урока обратить внимание на высказывание Математику уже затем учить надо, что она ум в порядок приводит.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 23
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Урок: Математическое моделирование
Предлагаю в начале урока обратить внимание на высказывание: «Математику уже затем учить надо, что она ум в порядок приводит» (М.Ломоносов).
– Что скажете? Согласны?
Хорошо, отлично! Настраиваемся на сегодняшнюю работу!
Наверное, на сегодняшний день нет такой области знаний, где бы не применялись дистижения математики. Физики и химики, астрономы и биологи, географы и экономисты, даже языковеды и историки используют математический аппарат.
В чем же секрет универсальности «математического инструмента?». Ответ очевиден: ключ к решению многих научных задач – их удачный перевод на язык математики.
Действительно, формулировки задач из разных областей знаний содержат нематематические понятия. Если математик участвует в решении задач, то он в первую очередь стреится перевести ее на «родной» язык.
А какой язык математики считают родным?
-Математический.
-Верно, т.е. язык формул, выражений, уравнений, неравенств и тд.
В начале урока предлагаю Вам решить следующую задачу: Найти, сколько нужно взять квадратных плиток со стороной 15 см, чтобы застелить пол ванной комнаты, размеры которой 3,3 м и 2,8 м
Давайте обсудим ход решения данной задачи. Что необходимо сделать?
-Перевести см в м, затем найти площадь плитки( 0,15*0,15=0,0225). После чего найти площадь ванной комнаты (3,3*2,8=9,24). Теперь необходимо площадь ванной комнаты разделить на площадь плитки (9,24/0,025=410,6666, т.е. 411 плиток). Можно ли записать решение данной задачи в виде выражения?
-Да, (3,3*2,8)/(0,15*0,15).
Мы с вами перевели данную задачу на математический язык с помощью выражения. Результат такого перевода называют математической моделью, а саму задачу – прикладной задачей.
Как вы думаете, какая тема сегодняшнего урока?
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ.
Верно!
Как вы думаете, что от вас ожидается на уроке?
– усвоить суть понятия «математическое моделирование»;
– научиться осуществлять математическое моделирование
Отлично, цель и задачи сформулированы.
Почему вам нужно знать, что такое «математическое моделирование»?
-Чтобы быть математически грамотным.
То есть наш урок пройдет по следующему плану:
1. Понятие математической модели задачи.
2. Схема решения задачи математическим моделированием.
3. Пример решения прикладной задачи математическим моделированием.
То есть как мы уже сказали, математическая модель- описание реального объекта или процесса языком математических понятий, отношений, формул, уравнений и др.
Перед вами таблица и я предлагаю вам провести исследование и выяснить, из каких этапов состоит решение прикладной задачи.
Этапы решения прикладной задачи:
1) Построение математической модели.
2) Решение математической задачи.
3) Анализ полученного результата, исходя из содержания прикладной задачи
Отлично, давайте разберем задачу.
Масса деревянной балки составляет 120 кг, а масса железной балки – 140 кг, причем железная балка на 1 м короче деревянной. Какова длина каждой балки, если масса 1 м железной балки на 5 кг больше массы 1 м деревянной?
I этап. Пусть длина деревянной балки равна х м, тогда длины железной составляет
(х – 1) м. Масса 1 м деревянной балки равна
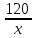кг, а масса 1 м железной 
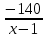кг. Тогда разность 
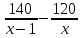показывает, на сколько масса 1 м железной балки больше массы 1 м деревянной балки. По условию задачи эта разность равна 5 кг. Тогда получаем уравнение 
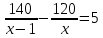. Это уравнение и является математической моделью данной прикладной задачи
II этап. Решение уравнения.
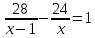
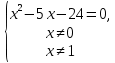
х = 8 или х = –3
III этап. Анализ результата, полученного на II этапе, исходя из содержания прикладной задачи.
Корень –3 не удовлетворяет условию задачи, поскольку такая величины, как длина, не может выражаться отрицательным числом. Следовательно, длина деревянной балки равна 8 м, а длина железной – 7 м.
Ответ: 8 м, 7 м.
Из двух пунктов, расстояние между которыми равно 18 км, вышли одновременно навстречу друг другу два туриста и встретились через 2 ч. С какой скоростью шел каждый турист, если для прохождения всего расстояния между пунктами первому из них нужно на 54 мин больше, чем второму?
Пусть скорость первого туриста равна х км/ч, а второго – у км/ч, х < у. До встречи первый турист прошел 2х км, а второй турист прошел 2у км. Вместе они прошли 18 км. Тогда 2х + 2у = 18.
Расстояние между пунктами первый турист проходит за
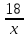ч, а второй – за 
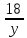ч. Так как первому туристу для прохождения этого расстояния нужно на 54 мин = =
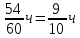больше, чем второму, то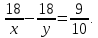
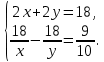
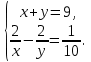
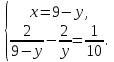
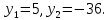
Корень
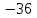не подходит по смыслу задачи. Следовательно, у = 5, х = 4, то есть скорость первого туриста 4 км/ч, а скорость второго 5 км/ч.Ответ: 4 км/ч, 5 км/ч.
– Два работника могут вместе выполнить производственное задание за 10 дней. После 6 дней совместной работы первого из них перевели на другое задание, а второй продолжал работать. Через 2 дня самостоятельной работы второго оказалось, что сделано
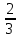всего задания. За сколько дней каждый работник может выполнить это производственное задание, работая самостоятельно?
Пусть первый работник может выполнить все задание за х дней, а второй – за у дней. За 1 день первый рабочий выполняет
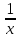часть задания, а за 10 дней – 
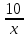часть задания. Второй работник за 1 день выполняет 
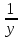часть задания, а за 10 дней – 
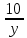часть задания. Так как за 10 дней совместной работы они выполняют все задание, то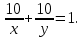 
Первый работник работал 6 дней и выполнил
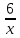часть задания, а второй работал 8 дней и выполнил 
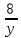часть задания. Так как в результате было выполнено 
задания, то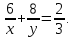 
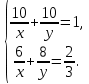
х = 15, у = 30.
Следовательно, первый работник может выполнить задание за 15 дней, а второй – за 30 дней.
Ответ: 15 дней, 30 дней.
Итак, что же такое математическое моделирование?
Из каких этапов состоит решение прикладной задачи?
Для чего нужно математическое моделирование?
Отлично! Что вам больше всего запомнилось на уроке? Довольны ли вы собой на этом уроке?
Домашняя работа на слайде. Отметки за урок:…..