Вопрос 1

Верно

Баллов: 1,000 из 1,000

Отметить вопрос

Текст вопроса

Общий интеграл дифференциального уравнения dyy=sinxdxdyy=sin⁡xdx имеет вид

Выберите один ответ:

ln|y|=cosx+Cln⁡|y|=cos⁡x+C

1y2=cosx+C1y2=cos⁡x+C

ln|y|=−cosx+Cln⁡|y|=−cos⁡x+C 

y=ecosx+Cy=ecos⁡x+C

Вопрос 2

Верно

Баллов: 1,000 из 1,000

Отметить вопрос

Текст вопроса

Дифференциальными уравнениями с разделяющимися переменными являются

Выберите один или несколько ответов:

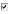x2y′+y=x+2x2y′+y=x+2 

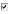y′=y2(x+1)y′=y2(x+1) 

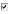5y′′−4y′+2y=cosx5y′′−4y′+2y=cos⁡x 

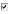xy′+2y=0xy′+2y=0 

(x+1)3y′=x(y+1)(x+1)3y′=x(y+1) 

Вопрос 3

Верно

Баллов: 1,000 из 1,000

Отметить вопрос

Текст вопроса

Общим интегралом дифференциального уравнения F(x,y,y′,…,y(n))=0F(x,y,y′,…,y(n))=0 является семейство функций вида

Выберите один ответ:

y=φ(x,C)y=φ(x,C)

Ф(x,y,C1,C2)=0Ф(x,y,C1,C2)=0

y=C1φ(x)+C2y=C1φ(x)+C2

---

Ф(x,y,C1,…,Cn)=0Ф(x,y,C1,…,Cn)=0 

Вопрос 4

Верно

Баллов: 1,000 из 1,000

Отметить вопрос

Текст вопроса

Решением задачи Коши y′−y=e2x,y′−y=e2x, y(0)=1y(0)=1 является функция

Выберите один ответ:

y=xexy=xex

y=e2x+xexy=e2x+xex

y=2ex−e2xy=2ex−e2x

y=ex(ex+1)y=ex(ex+1)

y=e2xy=e2x 

Вопрос 5

Верно

Баллов: 1,000 из 1,000

Отметить вопрос

Текст вопроса

Сумма параметров αα и β,β, при которых уравнение y′′+(y′′)α−β+5⋅y′+exy=x(8−2β)y′′+(y′′)α−β+5⋅y′+exy=x(8−2β) является линейным однородным дифференциальным уравнением, равна

Ответ: 

Вопрос 6

Неверно

Баллов: 0,000 из 1,000

Отметить вопрос

Текст вопроса

Общее решение линейного однородного дифференциального уравнения y′′−2y′+2y=0y′′−2y′+2y=0 имеет вид

Выберите один ответ:

ex(C1cosx+C2sinx)ex(C1cos⁡x+C2sin⁡x)

C1ex+C2e−xC1ex+C2e−x 

C1cosx+C2sinxC1cos⁡x+C2sin⁡x

e−x(C1cosx+C2sinx)e−x(C1cos⁡x+C2sin⁡x)

Вопрос 7

Верно

Баллов: 1,000 из 1,000

Отметить вопрос

Текст вопроса

Уравнениями с разделяющимися переменными являются уравнения вида

Выберите один или несколько ответов:

---

y′=f(x,y)y′=f(x,y) 

y′=xmf(x,y)y′=xmf(x,y) 

p(y)dy=q(x)dxp(y)dy=q(x)dx 

y′=p(x)q(y)y′=p(x)q(y) 

Вопрос 8

Верно

Баллов: 1,000 из 1,000

Отметить вопрос

Текст вопроса

Замена Бернулли для решения линейного дифференциального уравнения первого порядка имеет вид

Выберите один ответ:

y=uv,y′=u′v+uv′y=uv,y′=u′v+uv′ 

y=ux,y′=u′x+uy=ux,y′=u′x+u

y=uv,y′=u′v−uv′v2y=uv,y′=u′v−uv′v2

y′=kyy′=ky

Вопрос 9

Неверно

Баллов: 0,000 из 1,000

Отметить вопрос

Текст вопроса

Порядок дифференциального уравнения 7y′′+y′−3y=x57y′′+y′−3y=x5 равен

Выберите один ответ:

22

33

55 

77

Вопрос 10

Верно

Баллов: 1,000 из 1,000

Отметить вопрос

Текст вопроса

Функция y=x(sinx+1)y=x(sin⁡x+1) является решением дифференциального уравнения

Выберите один ответ:

y′=(1−y)cosxy′=(1−y)cos⁡x

y′=cos(y−x)y′=cos⁡(y−x)

xy′=y+xsinx

---

 

---

Смотрите также файлы

• Жизнь египтян всегда была тесно связана с рекой Нил.docx

• Критомикенская цивилизация.doc

• Отчет о практике по финансам предприятия.doc

• Ключевые слова Информация Виды информации Действия с информацией Что такое информация.ppt

• Отчет по учебной практике научноисследовательская работа.docx