Файл: Отчет по лабораторной работе по дисциплине Вероятностные модели инфокоммуникационных процессов Студента заочного отделения.doc

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Отчет по практике

Дисциплина: Не указана

Добавлен: 03.12.2023

Просмотров: 13

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

ФЕДЕРАЛЬНОЕ Государственное АВТОНОМНОЕ образовательное УЧРЕЖДЕНИЕ ВЫСШЕГО образования

БЕЛГОРОДСКИЙ ГОСУДАРСТВЕННЫЙ НАЦИОНАЛЬНЫЙ

ИССЛЕДОВАТЕЛЬСКИЙ УНИВЕРСИТЕТ

(НИУ «БелГУ»)

ИНСТИТУТ ИНЖЕНЕРНЫХ И ЦИФРОВЫХ ТЕХНОЛОГИЙ
КАФЕДРА ИНФОРМАЦИОННО-ТЕЛЕКОММУНИКАЦИОННЫХ СИСТЕМ И ТЕХНОЛОГИЙ

Отчет по лабораторной работе по дисциплине: Вероятностные модели инфокоммуникационных процессов

Студента заочного отделения

2 курса 12002153 группы

Пасивенко А.Ю.
Проверил:

Асс. Ст. Пр. Голощапова В.А.

Белгород 2023

Лабораторная работа №1. Экспериментальный анализ одномерной случайной величины



Цель работы: «Приобретение практических навыков по статистической обработке результатов наблюдений и ознакомление с основными характеристиками одномерной случайной величины»

Содержание отчета к работе:

Данные приведенные ниже варианты заданий (таблица 1), представляют собой выборку из результатов наблюдений одномерной случайной величины объемом пятьдесят значений).

Таблица 1 – Варианты заданий к лабораторной работе №1

№ п/п
Вар 1
Вар 2
Вар 3
Вар 4
Вар 5
Вар 6
Вар 7
Вар 8
Вар 9
Вар 10
Вар 11
Вар 12
Вар 13
Вар 14
Вар 15
Вар 16
Вар 17
Вар 18
Вар 19
Вар 20




1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

1
5
3
7
12
7
4
6
2
10
9
5
3
7
12
4
7
6
2
10
9

2
2
8
6
10
9
9
7
7
8
5
2
8
6
10
9
9
7
7
2
5

3
7
14
5
9
9
6
0
10
2
7
7
14
5
9
6
9
0
10
2
7

4
5
4
7
14
13
7
13
7
2
4
5
4
7
14
7
13
13
7
2
4

5
6
1
3
1
6
10
6
7
3
2
6
1
3
1
10
6
6
7
3
2

6
2
4
6
7
4
6
5
8
1
7
2
4
6
7
6
4
5
8
1
7

7
2
7
3
4
7
8
8
4
1
4
2
7
3
4
8
7
8
4
1
4

8
6
7
8
1
11
3
12
7
4
7
6
7
8
1
3
11
12
7
4
7

9
5
11
5
7
12
8
2
8
6
13
5
11
5
7
8
12
2
8
6
13

10
4
10
5
14
13
7
11
6
2
4
4
10
5
14
7
13
11
6
2
4

11
3
6
4
7
9
1
12
6
5
6
3
6
4
7
1
9
12
6
5
6

12
6
8
3
5
9
3
10
11
2
8
6
8
3
5
3
9
10
11
2
8

13
3
6
5
3
8
10
9
7
3
4
3
6
5
3
10
8
9
7
3
4

14
2
8
5
13
12
10
8
6
6
7
2
8
5
13
10
12
8
6
6
7

15
2
6
5
5
12
6
16
5
3
7
2
6
5
5
6
12
16
5
3
7

16
4
1
5
6
13
8
11
12
4
8
4
1
5
6
8
13
11
12
4
8

17
2
8
5
4
13
8
13
8
4
1
2
8
5
4
8
13
13
8
4
1

18
4
10
6
1
8
9
8
10
1
3
4
10
6
1
9
8
8
10
1
3

19
6
14
5
3
5
6
11
2
3
3
6
14
5
3
6
5
11
2
3
3

20
5
9
5
13
10
8
10
12
2
2
5
9
5
13
8
10
10
12
2
2

21
1
6
3
5
13
7
8
7
6
7
1
6
3
5
7
13
8
7
6
7

22
7
13
8
3
5
7
9
11
3
10
7
13
8
3
7
5
9
11
3
10

23
4
1
1
2
5
8
5
5
6
9
4
1
1
2
8
5
5
5
6
9

24
5
0
5
13
8
7
11
12
4
9
5
0
5
13
7
8
11
12
4
9

25
3
13
8
9
5
10
5
7
7
7
3
13
8
9
10
5
5
7
7
7

26
3
2
6
13
12
7
10
2
5
5
3
2
6
13
7
12
10
2
5
5

27
3
5
8
11
9
5
6
4
3
5
3
5
8
11
5
9
6
4
3
5

28
2
14
5
7
2
9
6
7
4
6
2
14
5
7
9
2
6
7
4
6

29
4
3
7
11
7
8
7
13
5
7
4
3
7
11
8
7
7
13
5
7

30
6
12
6
5
8
4
3
12
3
11
6
12
6
5
4
8
3
12
3
11

31
1
1
6
11
3
8
12
4
7
6
1
1
6
11
8
3
12
4
7
6

32
2
12
9
6
5
11
9
11
1
3
2
12
9
6
11
5
9
11
1
3

33
3
6
4
4
4
4
9
5
2
8
3
6
4
4
4
4
9
5
2
8

34
3
11
3
13
5
10
7
6
1
10
3
11
3
13
10
5
7
6
1
10

35
3
7
4
4
11
9
13
5
6
7
3
7
4
4
9
11
13
5
6
7

36
5
3
2
2
4
12
8
8
4
0
5
3
2
2
12
4
8
8
4
0

37
1
4
9
2
6
12
5
6
6
–1
1
4
9
2
12
6
5
6
6
–1

38
4
11
7
8
11
4
7
5
2
6
4
11
7
8
4
11
7
5
2
6

39
4
8
5
7
4
4
12
6
2
5
4
8
5
7
4
4
12
6
2
5

40
4
3
7
4
9
5
5
11
5
5
4
3
7
4
5
9
5
11
5
5

41
11
12
6
6
8
6
6
5
2
4
11
12
6
6
6
8
6
5
2
4

42
8
4
4
13
6
7
5
6
4
–1
8
4
4
13
7
6
5
6
4
–1

43
7
5
4
8
7
5
10
6
2
6
7
5
4
8
5
7
10
6
2
6

44
3
9
6
10
12
4
4
10
6
5
3
9
6
10
4
12
4
10
6
5

45
0
9
6
10
10
7
10
4
3
4
0
9
6
10
7
10
10
4
3
4

46
6
10
5
7
6
6
6
4
8
2
6
10
5
7
6
6
6
4
8
2

47
1
10
6
10
13
6
5
6
2
6
1
10
6
10
6
13
5
6
2
6

48
5
8
8
14
5
4
6
3
6
6
5
8
8
14
4
5
6
3
6
6

49
4
8
7
3
6
8
13
8
1
7
4
8
7
3
8
6
13
8
1
7

50
3
0
8
7
5
5
7
5
6
6
3
0
8
7
5
5
7
5
6
6


1. Построить вариационный ряд:

Вариационный ряд 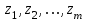получается из исходных данных путём сортировки значений экспериментальных данных 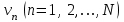в порядке возрастания от 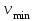до 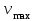так чтобы 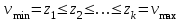и .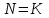
Пусть имеется выборка из 10 наблюдений (N = 10): x1 = 5, х2 = 2, х3 = 4, х4 = 5, х5 = 7, х6 = 3, х7 = 6, х8 = 8. х9 = 3, x10 = 9. Тогда им соответствует вариационный ряд z1 = 2, z2 = 3, z3 = 3, z4 = 4, z5 = 5, z6 = 5, z7 = 6, z8 = 7, z9 = 8, z10 = 9.
2. Оценить математическое ожидание:

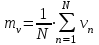, (1)

где 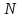 – кол-во значений экспериментальных данных;

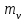 – среднее значение экспериментальных данных (математическое ожидание).

3. Оценить дисперсию.

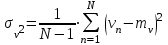(2)

где 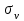 – разброс значений экспериментальных данных (дисперсия).
Вычислим дисперсию (  для следующего ряда: 2, 4, 6, 8, 10. Прежде всего, найдем среднее (М) для данного ряда, оно равно 6.

Из каждого элемента ряда вычтем величину среднего этого ряда. Полученные величины характеризуют то, насколько каждый элемент отклоняется от средней величины в данном ряду. Экспериментальные данные этой задаче, необходимые для расчета дисперсии, представим в виде (табл. 5)





4. Центрировать вариационного ряда.

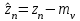= 8 – 5 = 3.

(3)
5. Нормировка вариационного ряда.


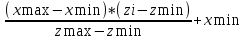(4)

Таблица 2 – Максимальное и минимальное значения

вариант

параметры
1
2
3
4
5

Максимальное значение
1
5
10
25
2

Минимальное значение
0
0
0
0
0

вариант

параметры
6
7
8
9
10

Максимальное значение
1
5
10
25
0

Минимальное значение
-1
-5
-10
-25
-2

вариант

параметры
11
12
13
14
15

Максимальное значение
7
6
32
43
-1

Минимальное значение
-7
-6
-32
-43
-6

вариант

параметры
16
17
18
19
20

Максимальное значение
10
100
1000
10
100

Минимальное значение
0
0
0
-10
-100

вариант

параметры
21
22
23
24
25

Максимальное значение
3
3
5
7
10

Минимальное значение
0
-3
1
-8
-100



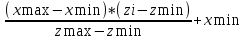= 1.2.

Контрольные вопросы

1. Дать определение случайной величины.

2. Дать определение математического ожидания.

3. Дать определение дисперсии.

4. Что произойдет с вариационным рядом, если все его члены разделить на первый элемент этого вариационного ряда.

5. Что произойдет с последовательностью если из каждого её члена вычесть среднюю величину.

6. Как найти центр распределения.

7. Что произойдет с последовательностью если каждый её член разделить на максимальный элемент.

8. Дать определение вариационного ряда.

9. Что произойдет с последовательностью если каждый её член разделить на максимальный элемент, а после каждый её член умножить на заданную величину.

10. Что произойдет с центром группирования ряда, если от каждого члена ряда отнять заданную величину.

1. Величина называется случайной, если она принимает свои значения в зависимости от исходов некоторого испытания (опыта), причем для каждого элементарного исхода она имеет единственное значение. Случайная величина называется дискретной (в узком смысле), если множество всех возможных значений ее конечно.

2.Математическое ожидание Mдискретной случайной величины — это среднее значение случайной величины, равное сумме произведений всех возможных значений случайной величины на их вероятности.

3. Дисперсия — это величина, показывающая, как именно и насколько сильно разбросаны значения — например, предсказания модели машинного обучения или доход за рассматриваемый период. За точку, относительно которой эти значения разбросаны, берут истинное значение, целевую переменную или математическое ожидание, которое вычисляется теоретически и заранее.

4. В результате статистической обработки материалов, полученных при измерении величины явления, можно подсчитать число единиц, обладающих конкретным значением того или иного признака.

Допустим, что в качестве изучаемого признака взят вес детали. Будем обозначать этот признак X. Измерения веса, например, 50 деталей дали следующие результаты (в г): 83, 85, 81, 82, 84, 82, 79, 84, 80, 81, 82, 82, 80, 82, 80, 82, 83, 84, 79, 79, 83, 82, 83, 85, 82, 82, 81, 80, 82, 82, .83,80, 82, 85, 81, 83, 81, 81, 83, 82, 81, 85, 83, 79, 81, 85, 81, 84, 81, 82.

5.Числовые последовательности


Термин «последовательность» используют, когда говорят о расположении учеников в шеренге, очередности дней недели, расположении команд в турнирной таблице и т. п. В этом параграфе мы выясним, что такое числовая последовательность, в частности, что такое арифметическая и геометрическая прогрессии, каковы их свойства, научимся использовать свойства упомянутых прогрессий при решении прикладных задач.

  • 1; 1; 2; 3; 5; 8;... — последовательность

  • 2; 5; 8; 11; 14;... — арифметическая прогрессия (каждое число, начиная со второго, на 3 больше предыдущего)

  • 2; 6; 18:54; 162:. . — геометрическая прогрессия (каждое число, начиная со второго, в три раза больше предыдущего)

6. К показателям центра распределения относятся: средняя арифметическая, мода и медиана.

Средняя арифметическая



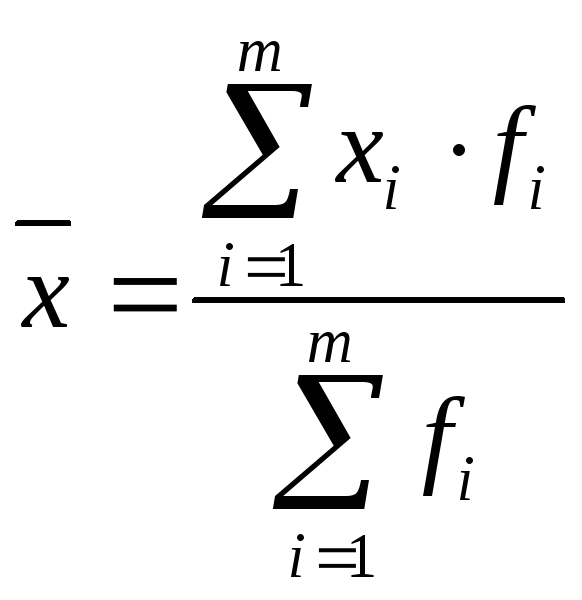
где xi –середина i-го интервала.



7.Последовательность — это набор из бесконечного количества элементов, которые занумерованы, т. е. имеют порядковые номера: 1, 2, 3, 4, 5 и так далее. То есть это, фактически, любая функция от натурального аргумента. Под числовой последовательностью обычно подразумевают таковую, состоящую из вещественных чисел. На последовательностях строится вся основа математического анализа, и им уделяется много внимания на первом курсе не только математических факультетов. И хотя представить себе «жизненное» применение самих по себе числовых последовательностей не так-то просто, мы постараемся уделить им достаточно много внимания примерами и демонстрациями, чтобы читатель мог составить о них полное представление.

8.Вариационный ряд — это статистический ряд, показывающий распределение изучаемого явления по величине какого-либо количественного признака.

Смотрите также файлы