Файл: Гемодинамика материалы к семинару Общая характеристика системы кровообращения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 75
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
За счет сил статического давления кровь движется вдоль кровеносных сосудов, из области повышенного давления в область пониженного: энергия статического давления переходит в кинетическую энергию движения крови. Силы давления крови на стенки кровеносных сосудов вызывают их упругую деформацию и соответствующий ей запас потенциальной энергии этого вида.
4.3.2. Гидростатическое давление-слагаемое ρgh. Выражение ρgh ассоциируется с выражением mgh потенциальной энергии тела массы m, находящегося на высоте h. И правильно делает, что ассоциируется. Гидростатическое давление ρgh – это и есть потенциальная энергия единицы объема жидкости, находящейся на высоте h; эта энергия обусловлена гравитационным притяжением к Земле жидкости, имеющей плотность ρ. Высоту h отсчитывают от уровня, условно принятого за нулевой.
Силы гравитации, создающие гидростатическое давление, и силы инерции, проявляющиеся в условиях перегрузок, знакомых военным летчикам, космонавтам, автогонщикам, - эти две силы бывают очень похожи по характеру вызываемых ощущений и могут оказаться вообще неотличимыми друг от друга. Перегрузка как измеряемая величина – это отношение ускорения a, которое испытывает, к примеру, летчик к величине ускорения свободного падения g. На время действия перегрузок в кровеносной системе и во всем организме действует дополнительное гидростатическое давление ρah. Оно действует не вместо давления ρgh, а наряду с ним. Но векторы a и g не всегда совпадают по направлению: Вектор g направлен к центру Земли, а вектор a имеет направление равнодействующей сил, приложенных к телу (возражать бесполезно: таков второй закон Ньютона).
При больших перегрузках система кровообращения может оказаться далеко за пределами условий, на которые она природой рассчитана. Считается, что организм без особых расстройств справляется с 8-кратной перегрузкой в течение трех секунд, а с 5-кратной – при ее продолжительности 12–15 секунд.
Для длительной работа кровеносной системы в условиях перегрузок требуются крепкое здоровье и тренировки на специальных тренажерах, например – на центрифуге.
Перегрузки неотличимы от возросшей гравитации как для человека, так и для любых измерительных приборов. Это утверждение соответствует принципу эквивалентности гравитации и инерции
, сформулированному Эйнштейном.
Пример – ситуация, знакомая многим по описаниям, кадрам кинохроники, и т.п.: Некто - на центрифуге. Его ощущения: чем больше скорость, тем сильнее «какая-то сила» вдавливает его в кресло, и ее называют силой инерции, а точнее – ее разновидностью: центробежной силой. Ему тяжело. Его ощущения – это ощущения как от реально действующей, все возрастающей силы тяжести. Но их можно объяснить с позиции стороннего наблюдателя, и тогда понятие центробежной силы становится лишним.
Вот показания стороннего наблюдателя: Некто залез в центрифугу, ее включили, она начала постепенно увеличивать скорость вращения. Некто стал вынужден двигаться по круговой траектории, и чем быстрее он двигался, тем тяжелее ему становилось: его удерживала на круговой траектории сила реакции его опоры – стенки центрифуги, и если бы не прочная стенка, лететь бы ему по касательной к своей круговой траектории в направлении чертей (собачьих). Так проявилась эквивалентность инерции и гравитации.
Чтобы испытать перегрузки, не обязательно становиться военным летчиком или космонавтом. Например, большие перегрузки испытывают участники дорожно-транспортных происшествий, их транспортные средства и пешеходы – участники ДТП. На рис. 3 приведена запись ускорения при краш-тесте легкового автомобиля.

По оси абсцисс – время в мс.
По оси ординат – ускорение
в единицах g.
Скорость перед ударом 52 км/час.
Максимальная перегрузка 70 g..
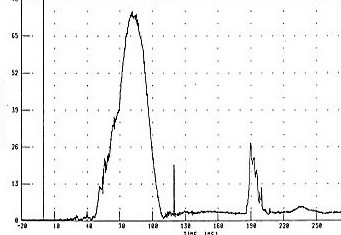
Рис. 3. Результаты краш-теста.
Уменьшение последствий столь больших перегрузок для водителей и пассажиров достигается увеличением длительности гашения их скорости с помощью ремней и подушек безопасности. Кое-что зависит при этом и от конструкции автомобилей: они не должны быть чрезмерно прочными, временной график их разрушения при аварии должен отвечать той же идее увеличения длительности удара.
4.3.3. Динамическое давление - слагаемое ρV2 / 2. У большинства это выражение ассоциируется с выражением для кинетической энергии: mV2 / 2. Ассоциация вполне уместная: динамическое давление – это кинетическая энергия единицы объема жидкости, имеющей скорость V.
Главная особенность динамического давления состоит в том, что оно
не является давлением в привычном смысле: оно не давит на стенки сосуда и на предметы, которые поток обтекает. Но оно проявит себя во всех своих паскалях при торможении потока: то, что до торможения было динамическим давлением, станет при торможении давлением статическим, действующим на остановившую поток преграду. В остановленном потоке динамическое давление равно нулю.
Вот пример проявления динамического давления. При измерениях артериального давления наблюдаются колебания стрелки манометра в такт с турбулентными шумами, которые прослушиваются на локтевом сгибе при «засечке» систолического давления. Они возникают в связи с появлениями и исчезновениями просвета в артерии, сжатой манжетой, при прохождении пульсовой волны. Кровь в просвете артерии, возникающем в моменты систолы, имеет большую скорость (порядка 4 м/с). Кратковременное появление динамического давления приводит, в соответствии с уравнением Бернулли, к кратковременному уменьшению статического давления крови на стенку артерии. Это повторяется при каждом сердечном сокращении. Стрелка манометра отслеживает пульсации статического давления. При этом максимальное давление крови в систоле – это тот максимум, который успевает показать колеблющаяся стрелка манометра и который следует записать как систолическое давление в протокол измерений.
4.3.4. Полное давление p0.
В уравнении Бернулли (4.3) p0 – полное давление на участке гидравлической сети. Мы убедились, что все три слагаемых полного давления имеют смысл различных видов механической энергии единичного объема текущей жидкости. Тогда полное давление – это полная механическая энергия единицы объема текущей жидкости, и энергетический смысл уравнения Бернулли состоит в следующем: полная механическая энергия стационарного потока жидкости есть величина постоянная, если потери энергии на преодоление сил трения пренебрежимо малы. При этом все три слагаемые полного давления p0 могут меняться, но непременно так, чти их сумма будет оставаться постоянной.
В качестве примера, иллюстрирующего полезность уравнения Бернулли, рассмотрим особенности водоснабжения в гидравлической линии постоянного поперечного сечения, проложенной в холмистой местности и представленной на рис. 4: ее участки находятся на разных уровнях.
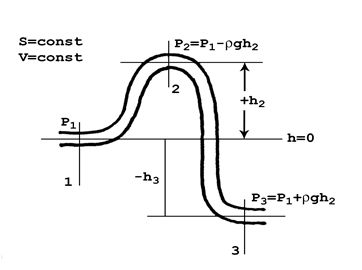
Рис.4. К уравнению Бернулли.
Положим, что насос, установленный на уровне h=0, поддерживает в сечении 1 постоянное статическое давление p1. Так как площадь сечения сети постоянна, то скорость V и динамическое давление ρV2/2 тоже постоянны.
Тогда уравнение Бернулли для участка между сечениями 1 и 2 запишется:
p1 + ρV2 / 2 + 0 = p2 + ρV2 / 2 + ρgh2 (4.4)
Здесь в левой части – полное давление в сечении 1, а в правой – в сечении 2. После сокращения одинаковых значений динамических давлений, получаем:
p1 = p2 + ρgh2
Отсюда следует:
p2 = p1 - ρgh2, то есть p2 ˂ p1 . (4.5)
Аналогично, для участка между сечениями 1 и 3 после сокращений уравнение Бернулли принимает следующий вид:
p1 = p3 - ρgh3,
Отсюда следует:

Заголовок на боковой панели]
[Боковые примечания — отличный способ вынести наиболее важные моменты из текста или разместить дополнительную информацию, чтобы ее можно было быстро найти (например, расписание).
Их можно располагать слева, справа, в верхней или нижней части страницы или перетаскивать в любое другое место.
Если вы готовы добавить свой текст — просто щелкните здесь и введите его.]
p3 = p1 + ρgh3, то есть p3 > p1. (4.6)
Мы убедились, что статическое давление в приподнятых участках гидравлической линии рис. 4 меньше, чем давление p1 на входе, а на опущенных оно, наоборот, превосходит входное.
Применительно к кровеносной системе: все, что находится выше уровня сердца, испытывает пониженное статическое давление (а это, в частности, мозг), а все, что ниже (ноги, например) - находится под давлением, превосходящим созданное сердцем. Для мозга действие гидростатического давления меняет статическое примерно на -30 мм рт. ст., а для ног эта «поправка» составляет около +110 мм рт. ст. Но система кровообращения имеет механизмы регулирования, вносящие поправки на снабжение кровью органов, находящихся в неравных условиях.
Движение крови в реальной кровеносной системе сопровождается не постоянством (как у Бернулли), а постепенным уменьшением полного давления крови: энергия сердечного сокращения расходуется на преодоление сил вязкого трения и других сил сопротивления. На подходе к
правому предсердию этот избыток давления, созданный левым желудочком, становится близким к нулю. Полное давление как сумма статического и динамического давлений, становится все меньше и наконец становится равным нулю:
р0 = р + ρV2/2 = 0 (4.7)
Отсюда следует, что если движение крови сохраняется, то статическое давление может оказаться отрицательным:
р = -ρV2/2 (4.8)
Этот результат означает, что давление в таких венах может быть несколько ниже атмосферного, и при их повреждении возможна воздушная эмболия – попадание воздуха в полости сердца. На реальном сердце такое статическое давление, которое можно называть разрежением, может составлять величину порядка - 3 мм рт. столба. Тонкостенные эластичные вены при этом временно спадают.