Файл: Зависимость собственных полупроводников и её зависимость от температуры.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 11
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Зависимость собственных полупроводников и её зависимость от температуры
Как мы уже видели, удельная проводимость выражается формулой
где n - концентрация носителей заряда, определяющих проводящие свойства данного тела, а u - подвижность этих носителей. Носителями заряда могут быть как электроны, так и дырки. Интересно отметить, что, хотя, как известно, у большинства металлов свободными носителями заряда являются электроны, у некоторых металлов роль свободных носителей заряда выполняют дырки. Типичными представителями металлов с дырочной проводимостью являются цинк, бериллий и некоторые другие.
Для выяснения зависимости проводимости от температуры необходимо знать температурную зависимость концентрации свободных носителей и их подвижности. В металлах концентрация свободных носителей заряда не зависит от температуры. Поэтому изменение проводимости металлов в зависимости от температуры полностью определяется температурной зависимостью подвижности носителей. В полупроводниках, напротив, концентрация носителей резко зависит от температуры, а температурные изменения подвижности практически оказываются незаметными. Однако в тех областях температур, где концентрация носителей оказывается постоянной (область истощения и область насыщения примесей), ход температурной зависимости проводимости полностью определяется температурным изменением подвижности носителей.
Значение же самой подвижности определяется процессами рассеяния носителей на различных дефектах кристаллической решетки, то есть изменением скорости направленного движения носителей при их взаимодействии с различными дефектами. Наиболее существенным является взаимодействие носителей с ионизированными атомами различных примесей и с тепловыми колебаниями решетки кристалла. В различных областях температуры процессы рассеяния, обусловленные этими взаимодействиями, сказываются по-разному.
В области низких температур, когда тепловые колебания атомов столь малы, что ими можно пренебречь, основное значение имеет рассеяние на ионизированных атомах примеси. В области же высоких температур, когда в процессе тепловых колебаний атомы решетки значительно смещаются от
положения устойчивого равновесия в кристалле, на первый план выступает тепловое рассеяние.
Рассеяние на ионизированных атомах примеси. В примесных полупроводниках концентрация примесных атомов во много раз превосходит концентрацию примесей в металлах. Даже при достаточно низкой температуре большая часть примесных атомов находится в ионизированном состоянии, что представляется вполне естественным, поскольку само происхождение проводимости полупроводников связано в первую очередь с ионизацией примесей. Рассеяние носителей на ионах примеси оказывается гораздо более сильным, чем рассеяние на нейтральных атомах. Объясняется это тем, что если рассеяние носителя на нейтральном атоме происходит при непосредственном столкновении, то для рассеяния на ионизированном атоме достаточно носителю попасть в область электрического поля, создаваемого ионом (рис. 28). Когда электрон пролетает сквозь область электрического поля, создаваемого положительным ионом, траектория его полета претерпевает изменение, как показано на рисунке; при этом скорость его направленного движения υЕ, приобретенная благодаря воздействию внешнего поля, уменьшится до Если электрон проходит достаточно близко около иона, то после рассеяния направление движения электрона может оказаться вообще противоположным направлению действия внешнего электрического поля.
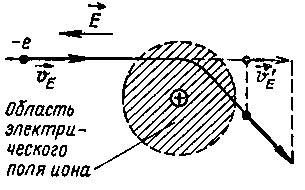
Рис. 28
Рассматривая задачу о рассеянии заряженных частиц на заряженных центрах, выдающийся английский физик Э. Резерфорд пришел к выводу, что длина свободного пробега частиц пропорциональна четвертой степени их скорости:
Применение этой зависимости к рассеянию носителей в полупроводниках привело к очень интересному и, на первый взгляд, неожиданному результату: подвижность носителей в области низких температур должна с повышением температуры расти. В самом деле, подвижность носителей оказывается пропорциональной кубу скорости их движения:
В то же время средняя кинетическая энергия носителей заряда в полупроводниках пропорциональна температуре
а, значит, средняя тепловая скорость пропорциональна корню квадратному из 
Следовательно, подвижность носителей находится в следующей зависимости от температуры:
В области низких температур, когда рассеяние на ионизированных примесях играет основную роль и когда тепловыми колебаниями атомов решетки можно пренебречь, подвижность носителей растет по мере повышения температуры пропорционально
(левая ветвь кривой u(Т) на рисунке 29). Качественно такая зависимость вполне объяснима: чем больше тепловая скорость носителей, тем меньше времени находятся они в поле ионизированного атома и тем меньше искажение их траектории. Благодаря этому возрастает длина свободного пробега носителей и увеличивается их подвижность.
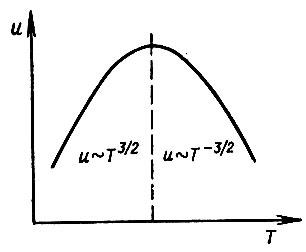
Рис. 29
Рассеяние на тепловых колебаниях. С повышением температуры средняя скорость теплового движения носителей возрастает настолько, что вероятность их рассеяния на ионизированных примесях становится очень малой. Вместе с этим амплитуда тепловых колебаний атомов решетки при этом возрастает, так что на первый план выступает рассеяние носителей на тепловых колебаниях. Благодаря росту рассеяния на тепловых колебаниях уменьшается по мере нагрева полупроводника длина свободного пробега носителей и, следовательно, их подвижность.
Конкретный ход зависимости
в области высоких температур для различных полупроводников неодинаков. Он определяется природой полупроводника, шириной запрещенной зоны, концентрацией примеси и некоторыми другими факторами. Однако для типичных ковалентных полупроводников, в частности для германия и кремния
, при не слишком больших концентрациях примеси зависимость u(T) имеет вид:
(см. правую ветвь кривой на рисунке 29).
Итак, подвижность носителей в полупроводниках в области низких температур растет прямо пропорционально
а в области высоких температур падает обратно пропорционально Зависимость проводимости полупроводника от температуры. Зная ход температурной зависимости подвижности и концентрации носителей в полупроводниках, можно установить характер температурной зависимости проводимости полупроводников. Схематически зависимость показана на рисунке 30. Ход этой кривой очень близок к ходу кривой зависимости приведенной на рисунке 25. Поскольку зависимость концентрации носителей от температуры гораздо сильнее температурной зависимости их подвижности, то в областях примесной проводимости (участок ab) и собственной проводимости (участок cd) зависимость удельной проводимости σ(T) практически полностью определяется ходом зависимости концентрации носителей от температуры. Углы наклона этих участков графика зависят соответственно от энергии ионизации атомов донорной примеси и от ширины запрещенной зоны полупроводника. Тангенс угла наклона γn пропорционален энергии отрыва пятого валентного электрона атома донорной примеси. Поэтому, получив экспериментально график изменения проводимости полупроводника при нагреве на примесном участке ab, можно определить значение энергии активации донорного уровня, то есть энергетическое расстояние донорного уровня Wd от дна зоны проводимости (см. рис. 20). Тангенс угла наклона γi пропорционален энергии перехода электрона из валентной зоны в зону проводимости, то есть энергии создания собственных носителей в полупроводнике. Таким образом, получив экспериментально ход зависимости проводимости от температуры на собственном участке cd, можно определить ширину запрещенной зоны Wg (см. рис. 17). Величины Wd и Wg являются важнейшими характеристиками полупроводника.
Основное различие между зависимостями σ(T) и n(T) наблюдается на участке bc, расположенном между температурой истощения примесей Ts и температурой перехода к собственной проводимости Ti. Этот участок соответствует ионизированному состоянию всех примесных атомов, а для создания собственной проводимости энергия тепловых колебаний оказывается еще недостаточной.
Поэтому концентрация носителей, будучи практически равной концентрации примесных атомов, не изменяется при увеличении температуры. Ход температурной зависимости проводимости на этом участке определяется ходом зависимости от температуры подвижности носителей. В большинстве случаев при умеренной концентрации примеси основным механизмом рассеяния носителей в этой области температур является рассеяние на тепловых колебаниях решетки. Этот механизм обусловливает уменьшение подвижности носителей и, следовательно, проводимости полупроводников с ростом температуры на участке bc.
В вырожденных полупроводниках благодаря большой концентрации примесей, обусловливающей перекрытие электрических полей ионов, рассеяние носителей на ионизированных атомах примеси сохраняет основное значение вплоть до высоких температур. А для этого механизма рассеяния как раз и характерно увеличение подвижности носителей с ростом температуры