Файл: Использование аттракторов.docx

Министерство образования и науки УкраиныГВУЗ «Приазовский государственный технический университет»Кафедра высшей и прикладной математикиКурсовая работапо дисциплине «Основы нелинейного анализа» на тему «Использование аттракторов»Мариуполь, 2018РЕФЕРАТПояснительная записка к курсовой работе ___с., ___рисунков, ___таблиц, ___приложений.Работа, посвящена решению задачи разложения сложных математических уравнений в иерархию бинарного дерева с последующим вычислением результата на электронной вычислительной машине.

Оглавление

Аттрактор Рёсслера

А 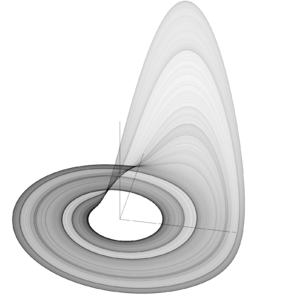ттрактор Рёсслера — хаотический аттрактор, которым обладает система дифференциальных уравнений Рёсслера: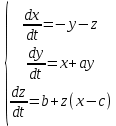Где a, b, c — положительные постоянные. При величине параметров a=b=0,2 и 2,6≤с≤4,2, уравнения Рёсслера имеют устойчивый предельный цикл. При данных значениях параметров период и форма предельного цикла совершают очередность удвоения периода. Сразу же за точкой с=4,2 появляется фактор хаотического аттрактора. 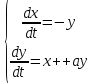Чётко определённые линии предельных циклов расплываются и заполняют фазовое пространство бесконечным счетным множеством траекторий, обладающим свойствами фрактала.Сам Рёсслер изучал систему при постоянных а=0,2, b=0.2и с=5.7, но также часто используются и значения а=0.1, b=0.1, и c=14.Иногда аттракторы Рёсслера строятся для плоскости, то есть с z=0.Устойчивые решения для х, у могут быть найдены с помощью вычисления собственного вектора матрицы Якоби вида

---

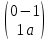
для которой

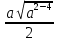
Вывод:

Найдём собственные значения матрицы



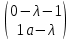
Определитель равен –λа+ 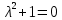, отсюда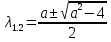



Таким образом, видно, что когда 0<a<2, собственные вектора являются комплексными и имеют положительные вещественные компоненты, что и делает аттрактор неустойчивым. Теперь будем рассматривать плоскость Z в том же диапазоне а. До тех пор, пока х меньше с, параметр с будет удерживать траекторию, находящуюся близко к плоскости х, у. Как только х станет больше с, z - координата увеличится, а чуть позже параметр - z будет тормозить рост х в .

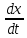Т очки равновесия

Для того, чтобы найти точки равновесия, три уравнения Рёсслера приравниваются нулю и x, y, z-координаты каждой точки равновесия находятся путём решения полученных уравнений. В итоге:



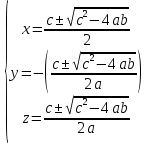
Как показано в общих уравнениях аттрактора Рёсслера, одна из этих фиксированных точек находится в центре аттрактора, а другие сравнительно далеко от центра.

Изменение параметров a, b и c

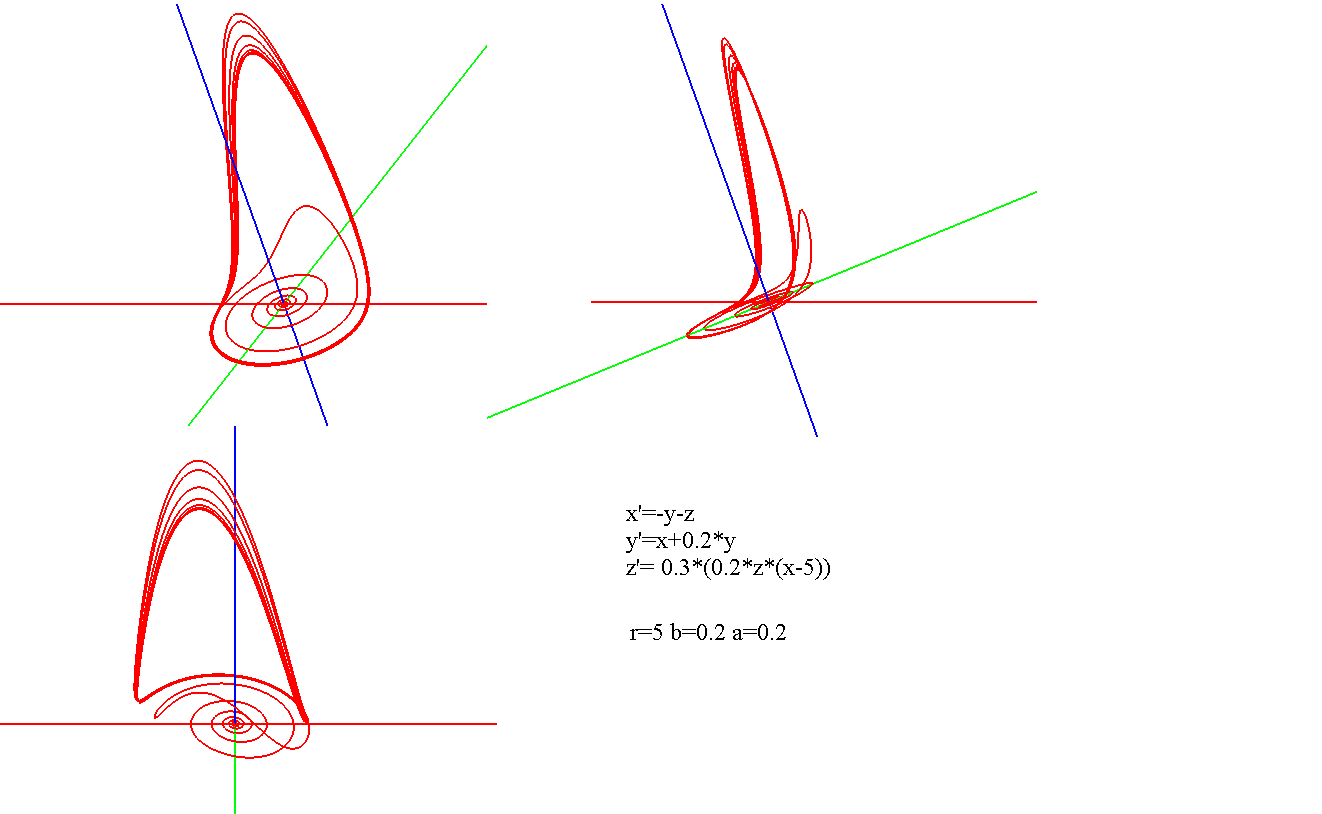
Поведение аттрактора Рёсслера существенно зависит от значений постоянных параметров. Изменение каждого параметра влечёт за собой определённый эффект, в следствие чего система может сойтись к периодической орбите, к неподвижной точке или устремиться в бесконечность. Численность периодов аттрактора Рёсслера определяется числом его витков вокруг центральной точки, которые возникают перед серией петель.

---

Бифуркационные диаграммы представляют собой стандартный инструмент для анализа поведения динамических систем, в которые включён и аттрактор Рёсслера. Они строятся методом решения уравнений системы, в которых закрепляются две переменные и изменяется одна. При построении такой диаграммы получаются практически полностью «закрашенные» области; это и есть область динамического хаоса.Изменение параметра aЗафиксируем c=0.2, c=5.7 и будем менять a.В итоге путём эксперимента получим такую таблицу:

• 
  а≤0: Сходится к устойчивой точке.
  
• 
  а=0.1Крутится с периодом 2.
  
• 
  а=0.2: Хаос (стандартный параметр уравнений Рёсслера).
  
• 
  а=0.3: Хаотичный аттрактор.
  
• 
  а=0.35: Аналогичен предыдущему, но хаос проявляется сильнее.
  
• 
  а=0.38: Аналогичен предыдущему, но хаос проявляется ещё сильнее.
  

Изменение параметра bЗапечатлеем a=b=0.1, с=5.7 и теперь начнем изменять параметр c. Как показывает рисунок, при стремящемся к нулю аттрактор неустойчив. Когда b станет больше a и с, система уравновесится и перейдёт в станционарное состояние.Изменение параметра cЗафиксируем a=b=0.1 и будем изменять c. Из бифуркационной диаграммы видно, что при маленьких показателях c система периодична, но при увеличении быстро становится хаотичной.

---

Аттрактор Лоренца

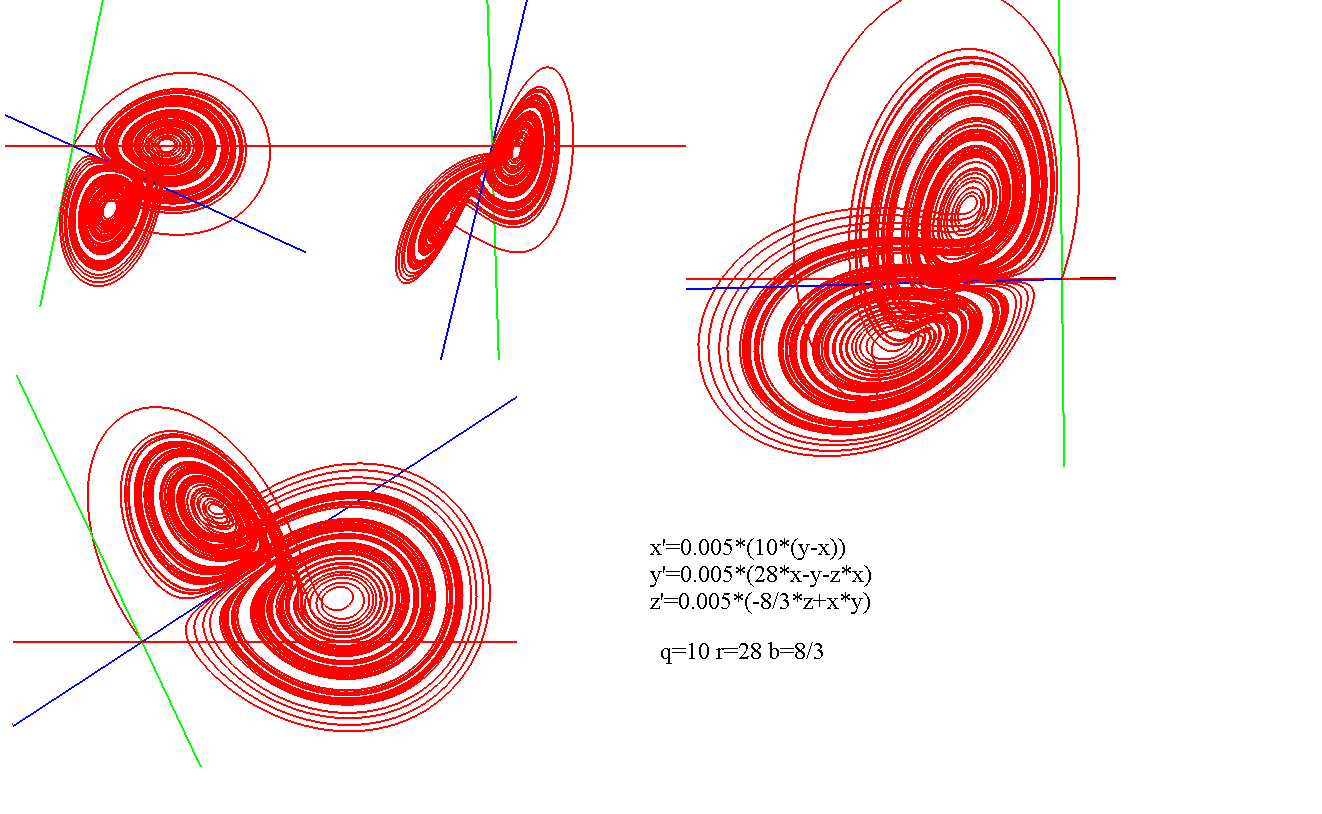
Аттрактор Лоренца ― компактное инвариантное множество L в трехмерном фазовом пространстве гладкого потока, которое имеет определённую сложную топологическую структуру и является асимптотически устойчивым, оно устойчиво по Ляпунову и все траектории из некоторой окрестности L стремятся к L при t → ∞(отсюда название).Аттрактор Лоренца был найден в его численных эксперимента, исследовавшего поведение траекторий нелинейной системы: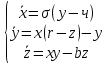при следующих значениях параметров: σ=10, r=28, b=8/3, x(0)=1, y(0)=0, z(0)=0. Эта система изначально была введена как первое нетривиальное галёркинское приближение для задачи о конвекции морской воды в плоском слое, чем и мотивировался выбор значений σ, r иb, но она возникает также и в других физических вопросах и моделях:

• 
  конвекция в замкнутой петле;
  
• 
  вращение водяного колеса;
  
• 
  модель одномодового лазера;
  
• 
  диссипативный гармонический осциллятор с инерционной нелинейностью.
  

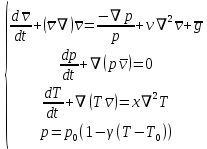
Исходная гидродинамическая система уравнений:Где 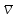— скорость течения, T — температура жидкости, 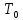— температура верхней границы (на нижней поддерживается 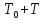, 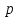— плотность, 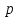— давление, 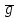— сила тяжести,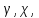υ— соответственно коэффициент теплового расширения, коэффициент температуропроводности и кинематической вязкости.В задаче о конвекции модель обнаруживается при разложении скорости течения и температуры в двумерные ряды Фурье и дальнейшей их «обрезки» с точностью до первых-вторых гармоник. Кроме того, приведённая полная система уравнений

---

гидродинамики записана в приближении Буссинеска. Обрезка рядов умеренно оправдана, так как Сольцмен в своих работах показал отсутствие каких-либо интересных особенностей в поведении большинства гармоник.

Осциллятор Ван дер Поля

Осциллятор Ван дер Поля — осциллятор с нелинейным затуханием, подчиняющийся уравнению 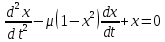, где Х — координата точки, зависящая от времени t;μ — коэффициент, характеризующий нелинейность и силу затухания колебаний.Двумерный случайСледуя теореме Льенара можно доказать, что система имеет предельный цикл. Из данной теоремы следует, 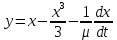. Отсюда можно вывести уравнения осциллятора Ван дер Поля для двумерного случая: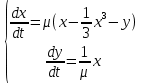Кроме этого можно совершить другую замену 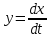и получить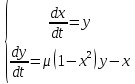Осциллятор со свободными колебаниямиУ осциллятора Ван дер Поля существуют два интересных режима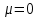: при и при 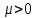Стоит отметить, что третьего режима — 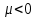— не существует, поскольку затухание в системе не может быть отрицательным.

1. 
   Когда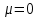 , то есть осциллятор рассчитывается без затухания, то указанные выше уравнения преобразуются к видy
   

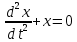.Это уравнение гармонического осциллятора.2) При 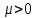система имеет определенные предельные циклы. Чем дальше

---