Файл: Лабораторная работа 1 Исследование разомкнутой линейной системы Цели работы.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 82
Скачиваний: 6
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Лабораторная работа № 1
Исследование разомкнутой линейной системы
Цели работы
-
освоение методов анализа одномерной линейной непрерывной системы с помощью среды Matlab
Задачи работы
-
ввести модель системы в виде передаточной функции -
построить эквивалентные модели в пространстве состояний и в форме «нули-полюса» -
определить коэффициент усиления в установившемся режиме и полосу пропускания системы -
научиться строить импульсную и переходную характеристики, карту расположения нулей и полюсов, частотную характеристику -
научиться использовать окно LTIViewer для построения различных характеристик -
научиться строить процессы на выходе линейной системы при произвольном входном сигнале
Оформление отчета
Отчет по лабораторной работе выполняется в виде связного (читаемого) текста в файле формата MicrosoftWord (шрифт основного текста Times New Roman, 12 пунктов, через 1,5 интервала, выравнивание по ширине). Он должен включать
-
название предмета, номер и название лабораторной работы -
фамилию и инициалы авторов, номер группы -
фамилию и инициалы преподавателя -
номер варианта -
краткое описание исследуемой системы -
результаты выполнения всех пунктов инструкции, которые выделены серым фоном (см. ниже): результаты вычислений, графики, ответы на вопросы.
При составлении отчета рекомендуется копировать необходимую информацию через буфер обмена из рабочего окна среды Matlab. Для этих данных используйте шрифт Courier New, в котором ширина всех символов одинакова.
Инструкция по выполнению работы
Основная часть команд вводится в командном окне среды Matlab. Команды, которые надо применять в других окнах, обозначены иконками соответствующих программ.
| Этап выполнения задания | Команды Matlab |
| clear all |
| clc |
| help tf |
| which('tf') |
| n = [n2 n1 n0] d = [1 d2 d1 d0] f = tf ( n, d ) |
| [n1,d1] = tfdata ( f, 'v' ) |
| z = zero ( f ) p = pole ( f ) |
| k = dcgain ( f ) |
| b = bandwidth ( f ) |
| f_ss = ss ( f ) |
| f_ss.d = 1 |
| k1 = dcgain ( f_ss ) |
| |
| f_zp = zpk ( f ) |
| who или whos (в чем разница?) |
| pzmap ( f ) |
| [wc,ksi,p] = damp ( f ) |
| ltiview |
| |
| ПКМ – Plot Types - Impulse |
| |
| |
| |
| |
| ПКМ – Plot Types – Step |
| ПКМ – Characteristics:
|
| |
| File – Print to Figure |
| print -dmeta |
| |
| |
| w = logspace(-1, 2, 100); |
| r = freqresp ( f, w ); r = r(:); |
| semilogx ( w, abs(r) ) |
| print -dmeta |
| |
| |
| [u,t] = gensig('square',4); |
| lsim (f, u, t) |
| print -dmeta |
| |
Таблица коэффициентов
| Вариант | | | | | | |
| | 1.0 | 1.10 | 0.100 | 3.0000 | 3.1600 | 1.2000 |
| | 1.1 | 1.54 | 0.495 | 2.8000 | 2.9200 | 1.2000 |
| | 1.2 | 1.08 | 0.096 | 2.3727 | 2.2264 | 0.9091 |
| | 1.3 | 1.04 | 0.091 | 2.1909 | 2.0264 | 0.9091 |
| | 1.4 | -1.54 | 0.252 | 1.8333 | 1.5278 | 0.6944 |
| | 1.5 | -0.90 | -0.240 | 1.6667 | 1.3611 | 0.6944 |
| | 1.6 | 0.80 | -0.224 | 1.3286 | 0.8959 | 0.4592 |
| | 1.7 | 1.36 | 0.204 | 1.1857 | 0.7673 | 0.4592 |
| | 1.8 | -1.98 | 0.432 | 1.2000 | 0.7644 | 0.3556 |
| | 1.9 | -0.76 | -0.399 | 1.3333 | 0.8711 | 0.3556 |
| | 2.0 | 0.60 | -0.360 | 1.2000 | 0.7406 | 0.2734 |
| | 2.1 | 1.68 | 0.315 | 1.3250 | 0.8281 | 0.2734 |
| | 2.2 | -2.42 | 0.616 | 1.3059 | 0.7696 | 0.2076 |
| | 2.3 | -0.46 | -0.552 | 1.4235 | 0.8401 | 0.2076 |
| | 2.4 | 0.24 | -0.480 | 1.3889 | 0.7531 | 0.1543 |
| | 2.5 | 2.25 | 0.500 | 1.5000 | 0.8086 | 0.1543 |
| | 2.6 | 0.26 | -0.780 | 1.2421 | 0.6139 | 0.1108 |
| | 2.7 | -0.27 | -0.810 | 1.1368 | 0.5717 | 0.1108 |
| | 2.8 | 0.28 | -0.840 | 0.8000 | 0.3700 | 0.0500 |
| | 2.9 | 3.19 | 0.870 | 0.7000 | 0.3500 | 0.0500 |
Контрольные вопросы к защите
-
Что такое
-
передаточная функция -
нули и полюса передаточной функции -
импульсная характеристика (весовая функция) -
переходная функция -
частотная характеристика -
модель в пространстве состояний -
модель вида «нули-полюса» -
коэффициент усиления в статическом режиме -
полоса пропускания системы -
время переходного процесса -
частота среза системы -
собственная частота колебательного звена -
коэффициент демпфирования колебательного звена
-
В каких единицах измеряются
-
коэффициент усиления в статическом режиме -
полоса пропускания системы -
время переходного процесса -
частота среза системы -
собственная частота колебательного звена -
коэффициент демпфирования колебательного звена
-
Как связана собственная частота с постоянной времени колебательного звена? -
Может ли четверка матриц
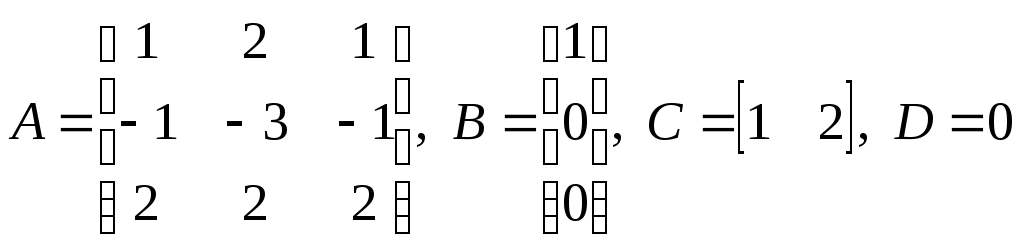
быть моделью системы в пространстве состояний? Почему? Какие соотношения между матрицами должны выполняться в общем случае?
-
Как получить краткую справку по какой-либо команде Matlab? -
В чем разница между командами Matlab
who и whos clear all и clc
-
Как ввести передаточную функцию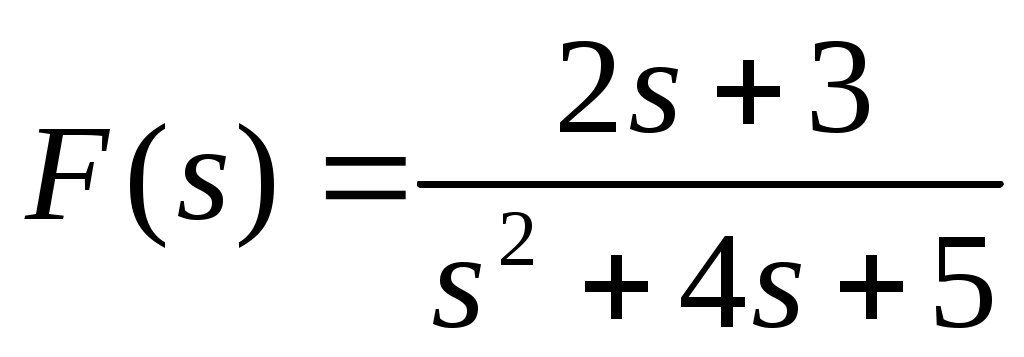 ?
? -
Как влияет изменение коэффициента прямой передачи (матрицы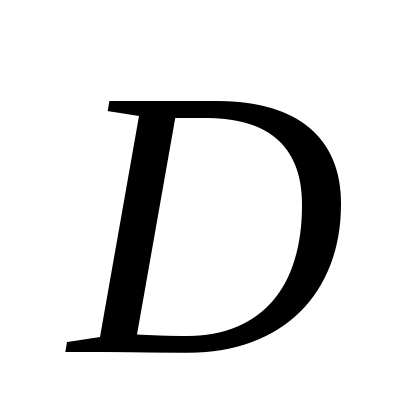 в модели в пространстве состояний) на статический коэффициент усиления?
в модели в пространстве состояний) на статический коэффициент усиления? -
Какие возможности предоставляет модуль LTIViewer? -
Что можно сказать об импульсной характеристике системы f_ss? Почему она не была построена верно? -
Как найти
-
коэффициент усиления в установившемся режиме по АЧХ -
полосу пропускания системы по АЧХ
-
Как скопировать график из окна Matlab в другую программу? -
Как построить массив из 200 значений в интервале от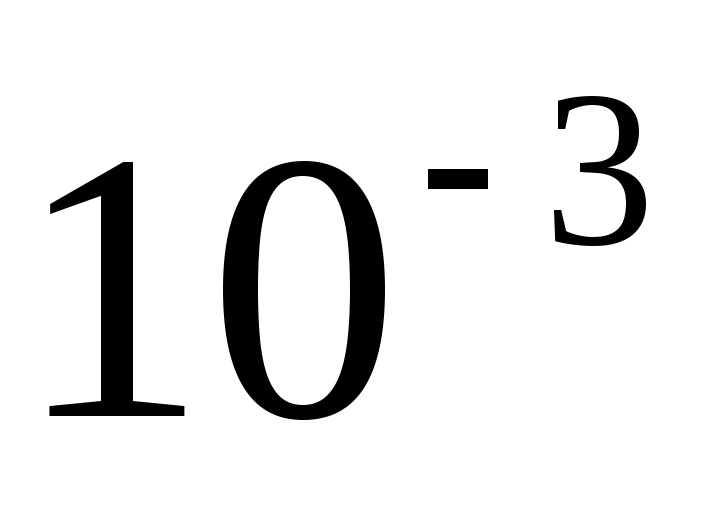 до
до 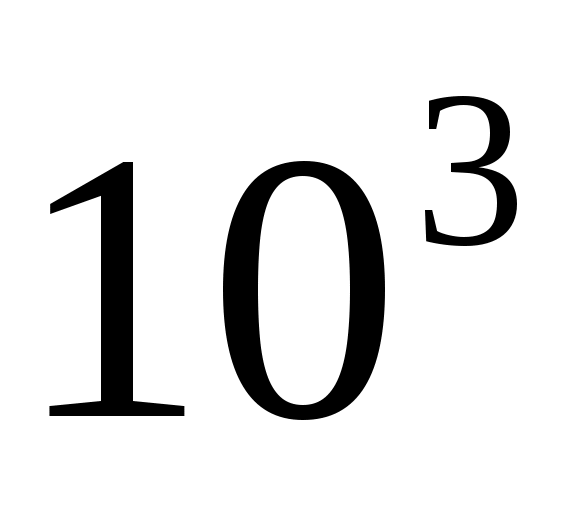 с равномерным распределением на логарифмической шкале?
с равномерным распределением на логарифмической шкале? -
Какие величины откладываются по осям на графике АЧХ?
Отчет по лабораторной работе № 1
Исследование разомкнутой линейной системы
-
Описание системы
Исследуется система, описываемая математической моделью в виде передаточной функции
-
Результаты исследования
-
адрес файла tf.m:
E:\MAT\LAB\toolbox\control\control\@tf\tf.m
-
нули передаточной функции
-0.6000
-0.5000
-
полюса передаточной функции
-0.2500 + 0.4330i
-0.2500 - 0.4330i
-0.2000
-
коэффициент усиления звена в установившемся режиме
k = 17.4000
-
полоса пропускания системы
b = 0.4808 рад/сек
-
модель системы в пространстве состояний
a =
-0.7000 -0.1750 -0.0500
2.0000 0 0
0 0.5000 0
b = 2
0
0
c = 1.4500 0.7975 0.4350
d = 0
-
статический коэффициент усиления после изменения матрицы
k1 = 18.4000
связь между k и k1 объясняется тем, что …
-
модель в форме «нули-полюса»
2.9 (s+0.6) (s+0.5)
----------------------------
(s+0.2) (s^2 + 0.5s + 0.25)
-
коэффициенты демпфирования и частоты среза
Полюс передаточной функции
Собственная частота, рад/сек
Постоянная времени, сек
Коэффициент демпфирования
-0.2000
-0.2500 + 0.4330i
-0.2500 - 0.4330i
0.2000
0.5000
0.5000
5
2
2
1.0000
0.5000
0.5000
-
Импульсные характеристики систем f и f_ss получились, одинаковые, потому что …
-
Переходные процессы исходной и модифицированной систем
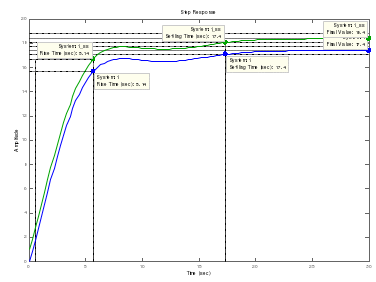
-
амплитудная частотная характеристика
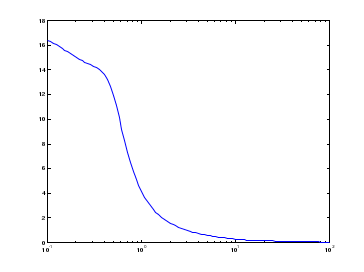
-
для того, чтобы найти статический коэффициент усиления по АЧХ, надо … -
для того, чтобы найти полосу пропускания по АЧХ, надо … -
реакция на сигнал, состоящий из прямоугольных импульсов
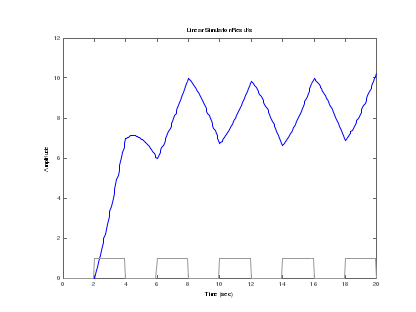
1 Все коэффициенты надо взять из таблицы в конце файла.
2 По умолчанию в Matlab время переходного процесса определяется для 2%-ного отклонения от установившегося значения.
3 Точка с запятой в конце команды подавляет вывод на экран результата выполнения. Это удобно при работе с большими массивами.
4 Частотная характеристика возвращается в виде трехмерного массива, в котором каждый элемент имеет 3 индекса: строка, столбец (для многомерных моделей) и номер точки частотной характеристики. Для системы с одним входом и одним выходом команда r = r(:); преобразует эти данные в в обычный одномерный массив.
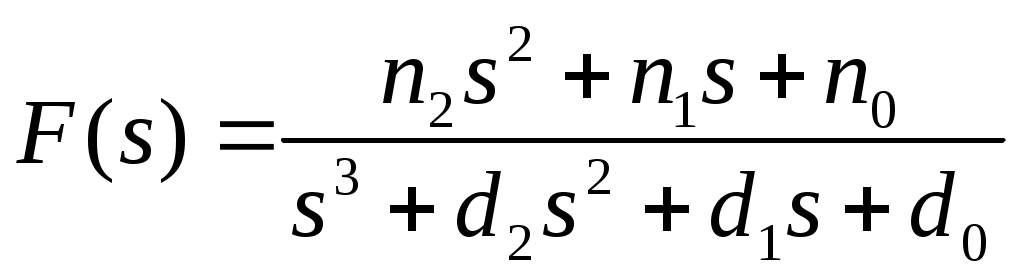 как объект tf.
как объект tf.