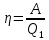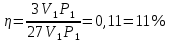Файл: Механика. Молекулярная физика. Термодинамика. Электростатика и постоянный ток.docx

Скачать файл (0,11Мб)

Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 03.12.2023

Просмотров: 15

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

федеральное государственное автономное образовательное учреждение

высшего образования

«Северный (Арктический) федеральный университет имени М.В. Ломоносова»

Высшая инженерная школа

^{(наименование высшей школы / филиала / института / колледжа)}

КОНТРОЛЬНАЯ РАБОТА №1

По дисциплине/междисциплинарному курсу/модулю		Физика


На тему	Механика. Молекулярная физика. Термодинамика. Электростатика и
постоянный ток

	Выполнил (-а) обучающийся (-аяся):
Щербаков Никита Алексеевич
^(Ф.И.О.)
	Направление подготовки / специальность:
15.03.02
^{(код и наименование)}
	Курс:	I
	Группа:	123201

	Руководитель:
Оруджова Ольга Низамиевна
^{(Ф.И.О. руководителя, должность / уч. степень / звание)}

Отметка о зачете
	^{(отметка прописью)}	^(дата)
Руководитель
	^{(подпись руководителя)}	^{(инициалы, фамилия)}

Архангельск 20

ЛИСТ ДЛЯ ЗАМЕЧАНИЙ

ОГЛАВЛЕНИ

Механика. Задача 3 4

Механика. Задача 33 5

Механика. Задача 53 6

Молекулярная физика. Термодинамика. Задача 13 7

Молекулярная физика. Термодинамика. Задача 33 7

Молекулярная физика. Термодинамика. Задача 53 9

Электродинамика. Задача 3 10

Электродинамика. Задача 13 10

Электродинамика. Задача 23 11

Электродинамика. Задача 33 12

Список использованных источнпков 14
Механика. Задача 3

Условие. По ледяной горке пустили скользить снизу вверх шайбу. На расстоянии l = 3 м от начальной точки шайба побывала дважды: через t₁ = 2 с и t₂ = 10 с после начала движения. Считая ускорение постоянным, найти его модуль и начальную скорость шайбы.

Дано	Решение
L_сп = L_под = 3 м t₁ = 2 c t₂ = 10 c a = const	1) Кинематические уравнения для подъёма и спуска шайбы представлены в формулах 1.1 и 1.2: (1.1) 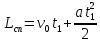(1.2) 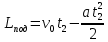2) Так как L_сп = L_под, правые части уравнений можно приравнять между собой: 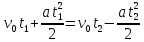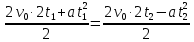3) Упрощая выражение, выведем формулу v₀(1.3): 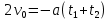(1.3) 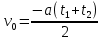4) Подставим формулу (3) в формулу (1) и упростим для получения формулы \|a\| (1.4): 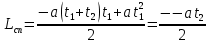(1.4) 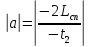5) Подставим исходные данные в формулы 1.3 и 1.4 и найдём требуемое: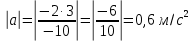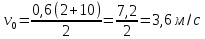
Найти: \|a\|, v₀	Ответ: \|a\| = 0,6 м/с², v₀ = 3,6 м/с

Механика. Задача 33

Условие. Шар диаметром 40 см вращается вокруг оси, проходящей через его центр, согласно уравнению φ = Аt + Bt², где B = 1,0 рад/с². Вращение происходит под действием силы F = 5 H, направленной по касательной к поверхности шара. Найти массу шара.

Дано	Решение
d = 0.4 м Уравнение движения: φ = Аt + Bt² B = 1,0 рад/с² F = 5 H	1) Исходя из уравнения движения (формула 2.1), получим производную угловой скорости (формула 2.2) (2.1) 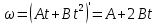(2.2) 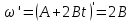2) Выразим массу, используя силу вращения, момент инерции и полученную ранее производную (формула 2.3): 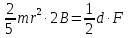(2.3) 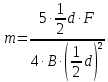3) Найдём массу, используя исходные данные: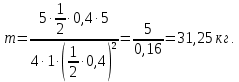
Найти: m	Ответ: m= 31,25 кг.

Механика. Задача 53

Условие. Два груза массами m₁ = 10 кг и m₂ = 15 кг подвешены на нитях длиной l = 2 м так, что грузы соприкасаются. Меньший груз был отклонен на угол φ = 60° и выпущен. Определить высоту h, на которую поднимутся оба груза после удара. Удар считать неупругим, грузы считать точечными.

Дано	Решение
m₁ = 10 кг m₂ = 15 кг l = 2 м g = 9,8 м/с² φ = 60°	1) Исходя из закона сохранения энергии и принимая, что в момент столкновения грузы попадают в состояние покоя, найдём скорость первого груза в момент столкновения со вторым (формула 3.1): 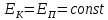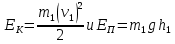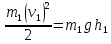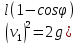(3.1) 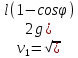2) Исходя из закона сохранения импульса, найдём скорость обоих грузов при их совместном движении (формула 3.2): (3.2) 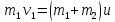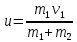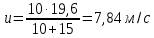3) Исходя из полученных ранее результатов, найдём высоту h (формула 3.3): (3.3)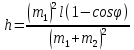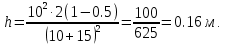
Найти: h	Ответ: h = 0,16 м

Молекулярная физика. Термодинамика. Задача 13

Условие. Определить среднюю кинетическую энергию вращательного движения одной молекулы двухатомного газа, если суммарная кинетическая энергия молекул 1 кмоля этого газа равна 3,01 МДж.

Дано	Решение
Е_К = 3,01·10⁶ Дж V = 1000 моль N_A = 6.023·10²³ моль I = 5 I_В = 2	1) Найдём среднюю кинетическую энергию всей молекулы, используя суммарную Е_к, V и N_А(формула 4.1): (4.1) 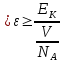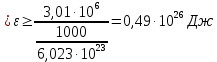2) Исходя из того, что газ двухатомный и принимая, что I = 5, а I_В = 2, найдём <ε_вр> (формула 4.2): (4.2)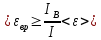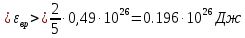
Найти: <ε_вр>	Ответ: <ε_вр> = 0,196 · 10²⁶ Дж

Молекулярная физика. Термодинамика. Задача 33

Условие. При изобарическом расширении одного моля некоторого газа, занимавшего объем 12 л при давлении 0,2 МПа, было подведено к газу 2,75 кДж теплоты, при этом газ совершил работу 1,1 кДж. Определить: а) параметры газа в конечном состоянии; б) из какого числа атомов состоят молекулы газа.

Дано	Решение
V = 1 моль V₁ = 1,2·10^-2 м³ P₁ = 2 · 10⁵ Па P = const Q = 2.75 · 10³ Дж A = 1.1 · 10³ Дж R = 8.31 Дж/(моль ∙ К)	1) Найдём изменение внутренней энергии в процессе, используя первый закон термодинамики (формула 5.1): (5.1) 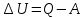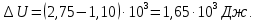2) Найдём новый объём газа, используя работу и давление газа (формула 5.2): (5.2) 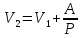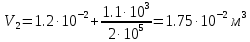3) Найдём изначальную температуру газа, используя уравнение идеального газа (формула 5.3): (5.3) 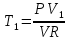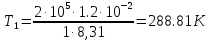4) Поскольку давление постоянно (процесс изобарический), конечную температуру найдём через соотношение объём-температура (формула 5.4): (5.4) 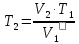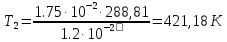5) Найдём число степеней свободы, выразив его из ∆U(формула 5.5): (5.5) 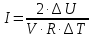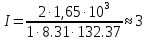Так как I = 3, газ одноатомный.
Найти: P_2,V_2,T₂, I	Ответ:P_2,= 2 · 10⁵Па, V₂ = 1,75 · 10^-2м³_,T₂ = 421,18 К, I = 3 (газ состоит из 1 атома)

Молекулярная физика. Термодинамика. Задача 53

Условие. Идеальный многоатомный газ совершает цикл, состоящий из двух изохор и двух изобар, причем наибольший объем в четыре раза больше наименьшего, а наибольшее давление газа в два раза больше наименьшего. Определить термический кпд цикла.

Дано	Решение
P₂ = 2P₁ V₂ = 4V₁ I = 6 (многоатомный газ)	1) Построим схему процесса (рисунок 1): 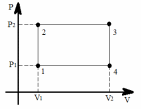Рисунок 1 - Термический процесс 2) Найдём работу, совершаемую газом, через объёмы и давления (формула 6.1): (6.1) 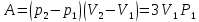(6.2) (6.3) 3) Найдём теплоту получаемую газом. Она будет равна сумме Qна участках 1-2 (формула 6.2) и 2-3 (формула 6.3): 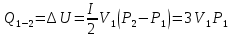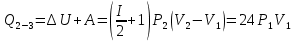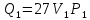(6.4) 4) Найдём термический КПД цикла (формула 6.4):
Найти: η	Ответ: η = 11%

Электродинамика. Задача 3

Условие. Две длинные прямые параллельные нити находятся на расстоянии d=5 см друг от друга, на нитях равномерно распределены заряды с линейными плотностями τ₁= 5 нКл/м и τ₂=10 нКл/м. Определить напряженность электрического поля Е в точке, удаленной от первой нити на расстояние r₁ = 3 см и от второй на расстояние r₂ = 4 см.

Дано	Решение
ε = 1 (вакуумная среда) ε₀ = 8,85·10^-12 Ф/м d= 0.05 м. τ₁ = 5 · 10^-9 Кл/м τ₂= 10 · 10^-9 Кл/м r₁ = 0.03 м. r₂ = 0,04 м.	1) Схема электродинамического процесса представлена на рисунке 2: 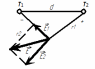Рисунок 2 - Электродинамический процесс 2) По принципу суперпозиции (формула 7.1): (7.1) 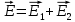3) Найдём модули E₁ и E₂по формулам 7.2 и 7.3: (7.2) 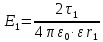(7.3) 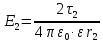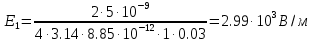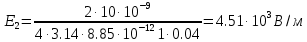4) Подставив полученное в формулу 7.1, получим: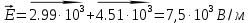
Найти: E	Ответ: E = 7,5 · 10³ В/м