Файл: Программа среднего профессионального образования 38. 02. 04 Коммерция (по отраслям) Дисциплина Математика.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 03.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Автономная некоммерческая организация профессионального образования «Открытый социально-экономический колледж»
Программа среднего профессионального образования
38.02.04 Коммерция (по отраслям)
Дисциплина: Математика
Практическое задание № 2
Выполнил:
слушатель Пшеничников Глеб Вячеславович
Преподаватель:
Васильцова Анна Сергеевна
Задание №1
Решить систему линейных уравнений методом Гаусса и методом Крамера:
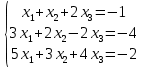
Решение:
1) Решим данную систему линейных уравнений методом Гаусса:
Составим расширенную матрицу системы уравнений. Она состоит из коэффициентов при неизвестных слева и столбца свободных членов справа.
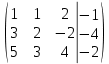
Метод Гаусса: при помощи элементарных преобразований приводят расширенную матрицу так, чтобы ниже главной диагонали основной матрицы были элементы обязательно равные нулю.
Элементарные преобразования- это:
1) Перемена местами двух строк (столбцов).
2) Умножение/деление строки (столбца) на число, отличное от нуля
3) Прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца).
С помощью нужных элементарных преобразований приведём расширенную матрицу так, чтобы ниже главной диагонали основной матрицы присутствовали только нулевые элементы.
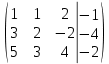
1. Для получения нулей в первом столбце ниже главной диагонали ко второй строке прибавим первую строку, умноженную на
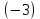 , к третьей строке прибавим первую строку, умноженную на
, к третьей строке прибавим первую строку, умноженную на 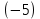 .
.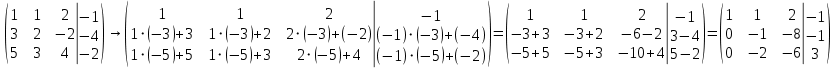
2. Для получения нулей во втором столбце ниже главной диагонали к третьей строке прибавим вторую строку, умноженную на
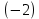 .
.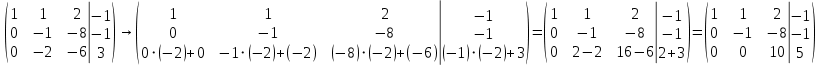
Количество ненулевых строк расширенной матрицы СЛУ после элементарных преобразований равно 3, поэтому ранг расширенной матрицы СЛУ системы равен 3.
Количество ненулевых строк основной матрицы СЛУ после элементарных преобразований равно 3, поэтому ранг основной матрицы СЛУ системы равен 3.
Количество неизвестных-
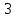 .
.Ранг основной матрицы СЛУ системы равен рангу расширенной матрицы СЛУ и равен количеству неизвестных, поэтому данная СЛУ имеет одно решение.
После элементарных преобразований получается СЛУ:
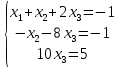
Находим
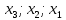 последовательно, начиная с последнего уравнения полученной СЛУ до первого уравнения полученной СЛУ.
последовательно, начиная с последнего уравнения полученной СЛУ до первого уравнения полученной СЛУ.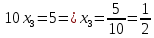
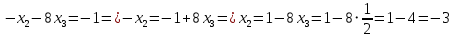
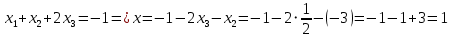
Тогда получаем решение данной СЛУ:
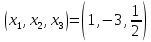
2) Решим данную систему линейных уравнений методом Крамера:
В чём заключается метод Крамера:
Если дана система линейных уравнений
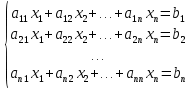
, тогда неизвестные
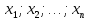 вычисляются по формулам:
вычисляются по формулам: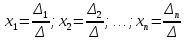 , где
, где 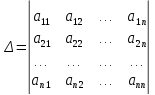 , причём
, причём 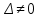
А остальные определители получаются, заменяя столбец с коэффициентами соответствующего неизвестного свободными членами.
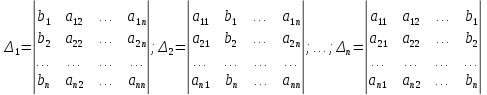
Запишем основную матрицу данной системы линейных уравнений, она состоит из коэффициентов при неизвестных:
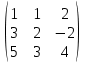 .
.Вычислим определитель основной матрицы данной системы линейных уравнений по правилу треугольников.
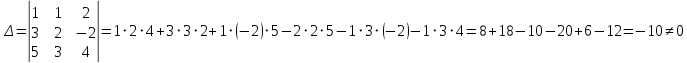
Определитель основной матрицы данной системы уравнений не равен нулю. => По теореме Крамера данная система линейных уравнений имеет единственное решение.
Найдём определители
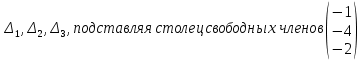 вместо первого, второго столбцов соответственно .
вместо первого, второго столбцов соответственно .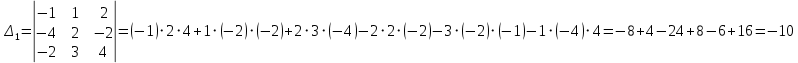
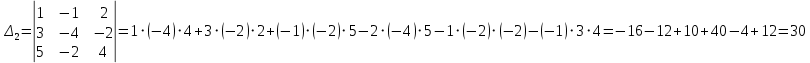
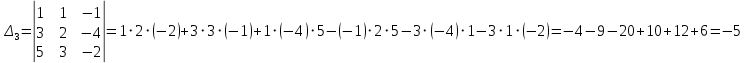
=> По формулам Крамера получаем данное решение системы линейных уравнений:
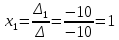 ;
; 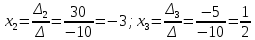
Ответ:

Задание №2
Решить систему линейных уравнений:
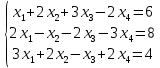
Решение:
Решим данную систему линейных уравнений методом Гаусса:
Составим расширенную матрицу системы уравнений. Она состоит из коэффициентов при неизвестных слева и столбца свободных членов справа.
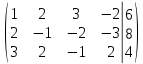
Метод Гаусса: при помощи элементарных преобразований приводят расширенную матрицу так, чтобы ниже главной диагонали основной матрицы были элементы обязательно равные нулю.
Элементарные преобразования- это:
1) Перемена местами двух строк (столбцов).
2) Умножение/деление строки (столбца) на число, отличное от нуля
3) Прибавление к элементам одной строки (столбца) соответствующих элементов другой строки (столбца).
С помощью нужных элементарных преобразований приведём расширенную матрицу так, чтобы ниже главной диагонали основной матрицы присутствовали только нулевые элементы.
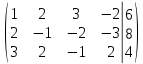
1. Для получения нулей в первом столбце ниже главной диагонали ко второй строке прибавим первую строку, умноженную на
 , к третьей строке прибавим первую строку, умноженную на
, к третьей строке прибавим первую строку, умноженную на
 , разделим третью строку на
, разделим третью строку на  для удобства дальнейших вычислений.
для удобства дальнейших вычислений.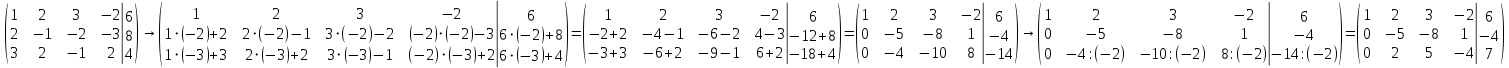
2. Для получения нулей во втором столбце ниже главной диагонали сначала умножим вторую строку на
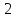 , умножим третью строку на
, умножим третью строку на 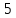 , а затем к третьей строке прибавим вторую строку, затем разделим вторую строку на (-2) и третью строку на (-9) для удобства дальнейших вычислений.
, а затем к третьей строке прибавим вторую строку, затем разделим вторую строку на (-2) и третью строку на (-9) для удобства дальнейших вычислений.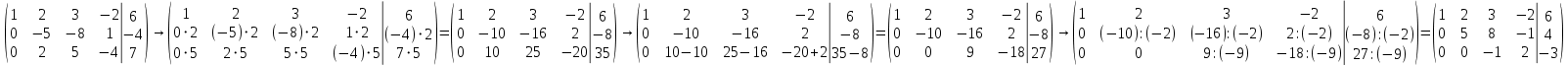
Вот и привели эту расширенную матрицу системы, так чтобы ниже главной диагонали расширенной матрицы все его элементы равны нулю.
Полученная расширенная матрица системы уравнений после элементарных преобразований соответствует системе уравнений:
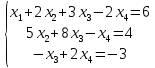
Ранг матрицы равен количеству ненулевых строк матрицы после элементарных преобразований.
Ранг расширенной матрицы системы (количество ненулевых строк расширенной матрицы после элементарных преобразований равно 3) равен рангу основной матрицы (количество ненулевых строк основной матрицы системы после элементарных преобразований равно 3) системы и равняется 3, но не равно количеству неизвестных системы линейных уравнений- это 4. => Система уравнений совместна и неопределенна (т.е. имеет бесконечное множество решений).
Количество базисных переменных равно рангу основной матрицы системы это 3. Тогда будет количество базисных переменных равно количеству неизвестных минус количество базисных переменных= 4-3=1.
На первых местах в ненулевых строках преобразованный матрицы системы расположены переменные
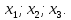 Тогда именно эти переменные
Тогда именно эти переменные 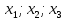 примем в качестве базисных, тогда будут свободные переменные
примем в качестве базисных, тогда будут свободные переменные 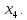
Пусть
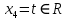 , так как
, так как 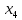 - это свободная переменная.
- это свободная переменная. Находим

последовательно, начиная с последнего уравнения полученной СЛУ до первого уравнения полученной СЛУ.
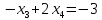 =>
=> 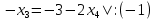 =>
=> 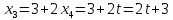
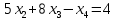 =>
=> 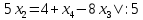 =>
=> 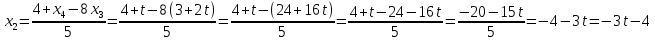
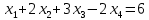 =>
=> 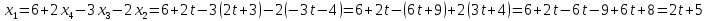
Окончательно получаем, что решение данной системы уравнений:
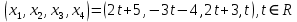
Ответ:
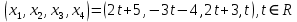
Тула – 2023