Добавлен: 03.12.2023
Просмотров: 31
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Федеральное государственное автономное образовательное учреждение высшего образования «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ»

13.03.01 «Теплоэнергетика и теплотехника»
Численное интегрирование
ОТЧЁТ
по дисциплине:
УИРС. Часть 1 . Семестр 3 (профиль Промышленная теплоэнергетика)
Направление: 13.03.01
Исполнитель:
студент группы 0-5Б02 Валеев Р.Р. 23.04.2023
Руководитель:
Преподаватель Бульба Е.Е.
Томск – 2023
Цель и задача работы
Цель работы: Ознакомление с сутью метода проектирования программных средств.
Задача работы: Решение задач при помощи ЭВМ согласно освоенному методу.
Этапы метода проектирования программных средств
Формулировка задачи – определить ее условия и ясно понять, что требуется для решения этой задачи. Отсеять второстепенные аспекты от основной сути задачи.
Анализ задачи – определить входные данные и выходные данные для решения этой задачи (полезно подчеркнуть фразы в формулировке задачи, идентифицирующие входные и выходные данные). Выбрать форму представления результатов решения (например, в виде таблицы) и составить список переменных, которые придется использовать при решении задачи с указанием взаимосвязей между ними.
Создание алгоритма решения задачи – запись пошаговых процедур (т.е. алгоритма). Например: 1) считывание данных; 2) выполнение вычислений; 3) вывод результатов.
После определения основных подзадач, каждую подзадачу можно разбить на более мелкие шаги – процесс, известный как детализация алгоритма.
Ручная отладка алгоритма – важная стадия в процессе создания алгоритма, однако, часто пренебрегают. Отладить вручную – значит мысленно выполнить каждый шаг алгоритма
, так как это впоследствии осуществит компьютер.
Реализация алгоритма – запись алгоритма в виде программы. При этом каждый шаг алгоритма преобразуется в один или несколько операторов того или иного языка программирования.
Структурное программирование – соблюдение общепринятого стиля программирования. Структурное программирование обеспечивает создание легких для понимания программ и снижает вероятность ошибок. Тестирование и отладка программы – позволяет добиться правильной работы программы. Запуск программы на ее выполнение несколько раз, с использованием наборов данных.
Поддержка и обновление программы – устранение ранее незамеченных ошибок и приведение ее в соответствие изменившимся государственным нормам или политике компании.
Задача 1. Численное интегрирование. Метод Симпсона
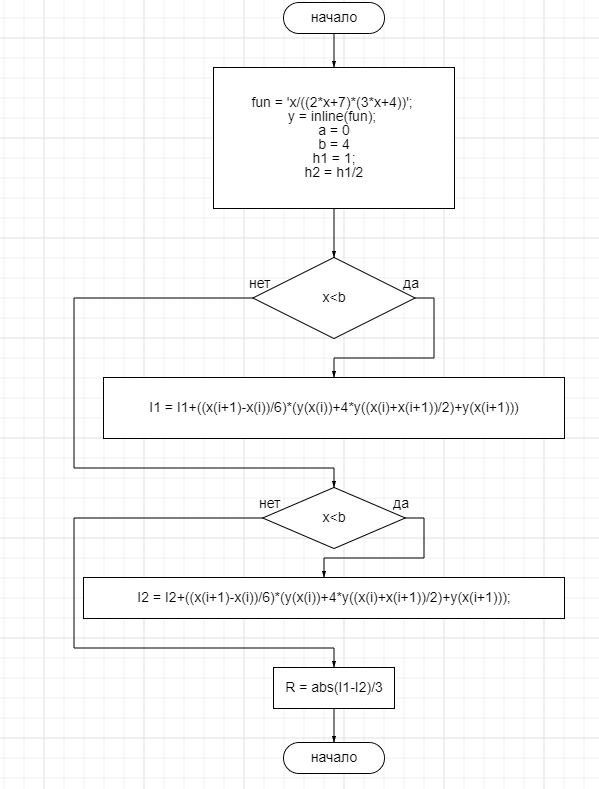
Рисунок 1 – метод Симпсона с проверкой точности
Код Matlab
%% исследуемые функции
fun = 'x/((2*x+7)*(3*x+4))'; % функция
y = inline(fun);
a = 0;
b = 4;
h1 = 1;
h2 = h1/2;
x = 0:h1:1;
n = length(x);
I1=0; %% диапазон расчета
%% метод симпсона
for i = 1:(n-1)
I1 = I1+((x(i+1)-x(i))/6)*(y(x(i))+4*y((x(i)+x(i+1))/2)+y(x(i+1)));
end
I1
x = 0:h2:1;
n = length(x);
I2=0;
%% метод симпсона
for i = 1:(n-1)
I2 = I2+((x(i+1)-x(i))/6)*(y(x(i))+4*y((x(i)+x(i+1))/2)+y(x(i+1)));
end
I2
%% оценка погрешности по методу Рунге
R = abs(I1-I2)/3
Вывод:
I1 = 0.0102
I2 = 0.0103
R = 1.3498e-05
Задача 2. Численное интегрирование. Метод Гаусса
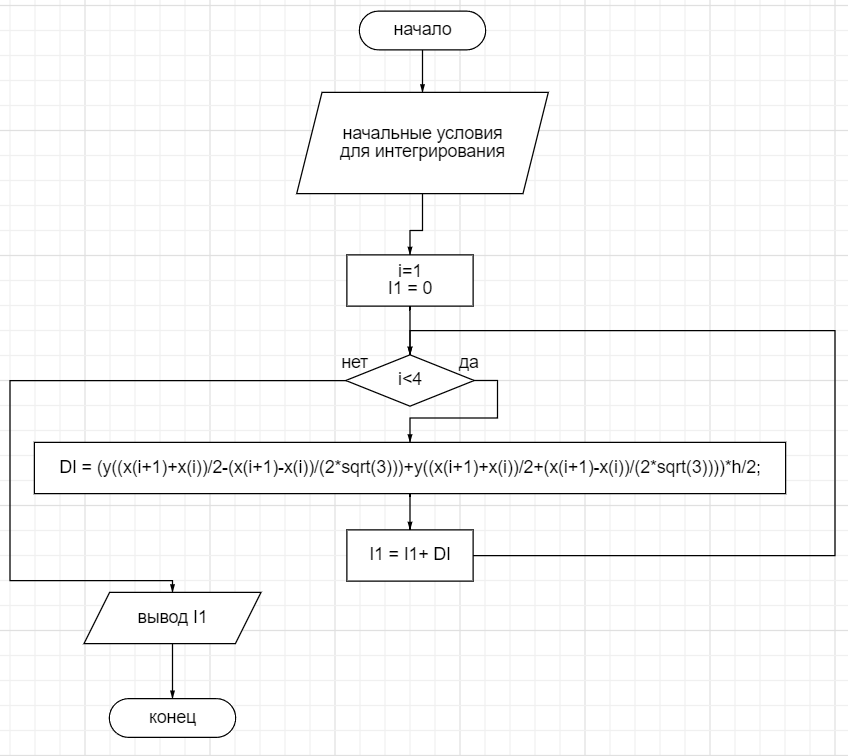
Рисунок 2 – блок-схема метода Гаусса
Код MATLAB
%% МЕТОД ГАУССА %%
clc
clear
warning('off');
fun = '1/(x+3)'; %% подинтегральная функция
y = inline(fun); %% функция
a = -1;
b = 1; %% диапазон интегрирования
j = 4; %% количество шагов
h = (b-a)/j;
x = a:h:b; %% шаг
%% Начало расчета %%
disp('Подынтегральная функция:')
disp(fun)
disp('Диапазон расчета:')
fprintf('a = %2.5f \n',a)
fprintf('b = %2.5f \n',b)
%% отрисовка подынтегральной функции
figure
for k = 1:length(x)
Y(k) = y(x(k));
end
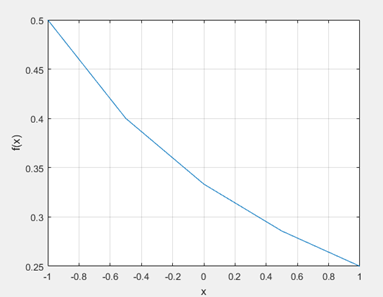
plot(x,Y)
grid on
xlabel('x');
ylabel('f(x)')
n = length(x);
I1=0;
for i = 1:(n-1)
DI = (y((x(i+1)+x(i))/2-(x(i+1)-x(i))/(2*sqrt(3)))+y((x(i+1)+x(i))/2+(x(i+1)-x(i))/(2*sqrt(3))))*h/2;
I1 = I1+ DI;
end
disp('значение интеграла')
disp(I1)
В
ывод:
Подынтегральная функция:
1/(x+3)
Диапазон расчета:
a = -1.00000
b = 1.00000
Значение интеграла = 0.6931
Рисунок 3 – график подынтегральной функции
Задача 3. Численное интегрирование с помощью степенных рядов.
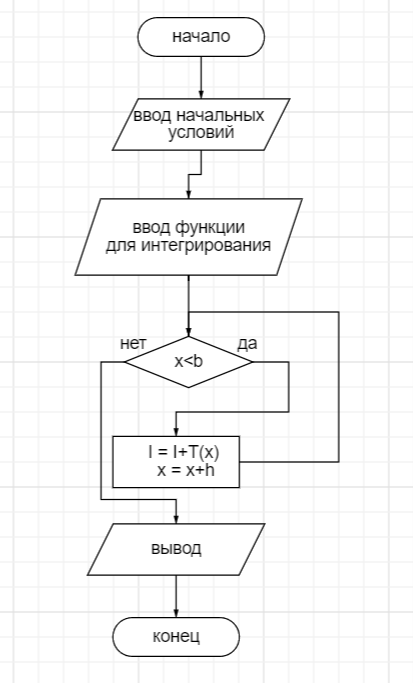
Рисунок 4 – блок-схема расчет интеграла через разложение в ряд
Код Matlab
%% численное интегрирование через разложение в ряд %%
clear
clc
syms x y
f = sin(x)/x
T = matlabFunction(taylor(f,x,1));
f2 = matlabFunction(f);
a = 0;
b = pi;
h = 0.01;
x = a;
I = 0;
while x
I = I+T(x);
x = x+h;
end
integral(f2,a,b) %% точное значение интеграла
I*h %% расчет через ряд
Вывод:
f = sin(x)/x
ans = 1.8519
ans = 1.8595
Задача 4.Расчет объёма тела методом Монте-Карло
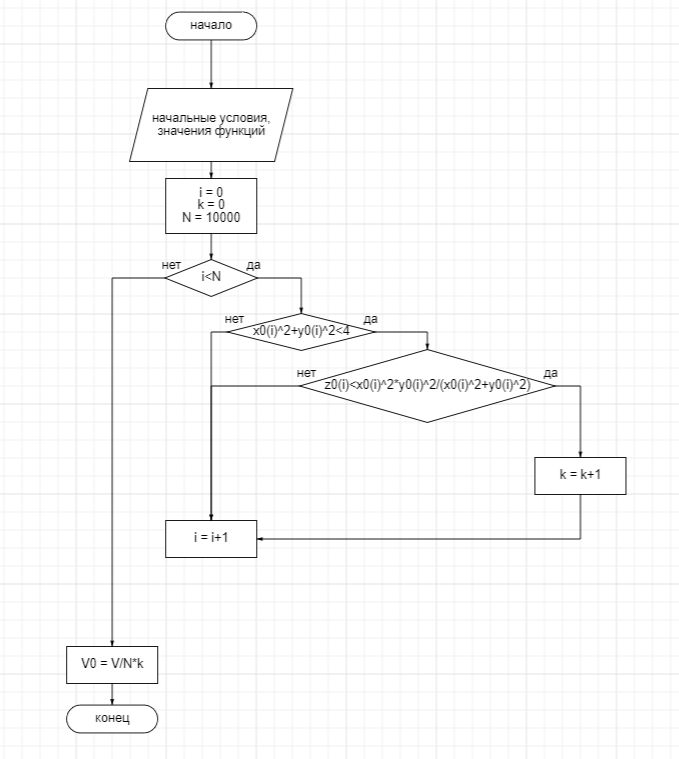
Рисунок 5 – блок-схема метода Монте-Карло
Код Matlab
%% метод Монте Карло
clear
clc
a_max = 2;
b_max = 2;
x = -2:0.1:2;
c_max = max(x.*x.*x.*x./(x.*x+x.*x));
V = a_max*2*b_max*2*c_max; %% расчет объёма куба
N = 10000;
k = 0; %% разброс точек
x0 = (rand(N,1)-0.5)*4;
y0 = (rand(N,1)-0.5)*4;
z0 = rand(N,1)*2;
plot(x0,y0,'r*')
%% подсчет точек внутри поверхности
for i = 1:N
if (x0(i)^2+y0(i)^2<4)
if (z0(i)
k = k+1;
end
end
end
%% объём поверхности
V0 = V/N*k0
Вывод:
V = 32
V0 = 3.2000
Заключение
В результате проделанной работы мной был освоен метод проектирования программных средств. Был усвоен алгоритм действий по решению задач при помощи ЭВМ. В частности был усвоен порядок действий при решении задач на написание программы по имеющейся блок-схеме, а также составлению блок-схемы по заданному тексту программы.
В целом решение задач позволило укрепить имеющиеся знания в области программирования на языке Matlab. Был усвоен поэтапный детальный способ решения задач, который позволил выполнять подобные задания более эффективно и быстро.