Работа № 6

ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТВЕРДОГО ТЕЛА

Приборы и принадлежности: маховик со шкивом; кронциркуль; груз с нитью; линейка; секундомер.

1. 
   Теоретическое введение
   

Кинетическая энергия вращающегося твердого тела T может быть рассчитана как сумма кинетических энергий отдельных его элементов. Имеем:

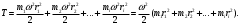(1)

Выражение, стоящее в скобках, называют моментом инерции J тела

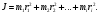(2)

Тогда равенство (1) будет иметь вид

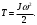(3)

Сопоставим полученное нами выражение (3) для кинетической энергии вращающегося тела с выражением для кинетической энергии тела, движущегося поступательно



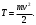
Мы видим, что момент инерции вращающегося тела имеет такое же физическое значение при вращательном движении, как масса тела при его поступательном движении, которая является мерой его инертности.

Анализ выражения (2) показывает, что инертность вращающегося тела зависит не только от массы, но и от того, как эта масса распределена относительно оси вращения. Это же выражение (2) показывает, что если мы будем иметь только одну вращающуюся точку с массой m, находящуюся на расстоянии от оси вращения, то ее момент инерции будет равен

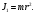(4)

Все слагаемые в формуле (2) суть моменты инерции отдельных материальных точек (элементов, на которые разбито тело). Следовательно, момент инерции тела равен сумме моментов инерции отдельных его точек (элементов).

Вычисление момента инерции тела представляет сложную задачу, так как приходится находить сумму бесконечно большого числа бесконечно малых слагаемых (массы материальных точек бесконечно малы). Для тел правильной геометрической формы эта задача решается методом интегрального исчисления. Существует ряд методов, позволяющих определить момент инерции тела экспериментально; один из них и будет использован в настоящей работе.

---

II. Описание аппаратуры и метода измерений

В настоящей работе опытным путем определяют момент инерции маховика А (металлического диска), насаженного на вал, на котором прикреплен шкив S. Вся система может вращаться около горизонтальной оси О₁О₂ (рис. 14). На шкиве S имеется небольшой штифтик, на который надевается петелька нити, на другом конце которой привязан груз m.

Наматывают нить на шкив, поднимая груз на высоту h от пола; в этом положении груз будет обладать (относительно пола) потенциальной энергией. Если отпустить маховик, то груз будет опускаться, двигаясь равноускорено и приводя во вращение систему: маховик, вал и шкив. При этом потенциальная энергия груза будет переходить в его кинетическую энергию, кинетическую энергию вращения системы и частично будет расходоваться на работу преодоления сил трения.

В тот момент, когда груз достигнет пола, его потенциальная энергия будет израсходована; тогда, применяя закон со

Хранения энергии, будем иметь

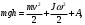(5)

где о – скорость груза в самой нижней точке пути; угловая скорость вращающейся системы в тот же момент: А – работа по преодолению сил трения за время движения груза.

Когда груз m достигает пола, нить соскакивает со шкива S; система продолжает вращаться. Вследствие наличия сил трения движение системы через некоторое время прекратится. Вся кинетическая энергия, которой обладала вращающаяся система в момент удара груза о пол, полностью переходит в работу против сил трения.

Будем считать, что работа сил трения пропорциональна числу оборотов; обозначим работу против трения при одном обороте через А₁. Обозначим через N₁, число оборотов системы за время падения груза m и через N₂ число оборотов от момента удара груза о пол до полной остановки системы. Тогда





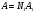
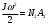
Из этих уравнений находим



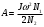
Внося это значение А в уравнение (5), получим

---

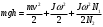
(6)

Скорость v груза при ударе о пол определится так:



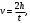
Где h – высота падения груза; t ­­­­­­­­­­­- время его падения. Так как нить намотана на шкив, то линейные скорости точек на поверхности шкива в любой момент равны скорости груза v.

Тогда для угловой скорости системы будем иметь



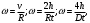
где R – радиус шкива S; D – диаметр шкива. Внося значения v и в выражение (6) и находя J, можно получить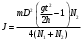



Практика лабораторных работ показывает, что обычно 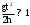и поэтому можно при вычислении J пользоваться упрощенной формулой

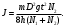(7)

Определяя величины, входящие в правую часть этого выражения, вычисляют момент инерции.

III. Порядок выполнения работы

1. 
   Знакомятся с установкой, измеряют диаметр шкива кронциркулем.
   
2. 
   Надевают на штифтик петлю нити, к которой привязан груз m. Вращая маховик рукою, опускают груз m так, чтобы оп только касался пола; точку касания отмечают мелом. Удерживая маховик в этом положении, проводят на нем мелом вертикальный радиус.
   
3. 
   Поднимают груз m. повернув маховик на несколько оборотов (их следует считать – это и будет N₁). Маховик останавливают в таком положении, когда отмеченный радиус вновь займет вертикальное положение.
   
4. 
   Удерживая маховик в этом положении, измеряют линейкой высоту и от нижнего края груза до отметки на полу.
   
5. 
   Определяют время t движения груза с высоты h; для этого одновременно отпускают маховик и включают секундомер: в момент удара груза о пол секундомер выключают.
   
6. 
   Предоставив маховику вращаться, считают число оборотов и, начиная от момента удара груза о пол до остановки. Для этой цели пользуются отмеченным радиусом.
   
7. 
   Опыты, описанные в пунктах 3, 4, 5 и 6, проделывают 10 раз, поднимая груз m на одну и ту же высоту; записывают все результаты в таблицу.
   
8. 
   Все опыты проделывают, изменив груз m.
   

---

IV. Обработка результатов опытов

1. 
   Находят средние значения времени падения t_ср и числа оборотов N_2cp.
   

Вычисляют среднее значение момента инерции I по формуле (7); величина массы m задана.

2. 
   Находят абсолютную погрешность измерения момента инерции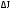 . Для этой цели вычисляют сначала относительную погрешность
   

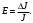
Из формулы (7) получаем

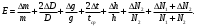(8)

Погрешностью 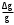можно пренебречь, так как она мала g по сравнению с остальными погрешностями. Погрешность AN, очень невелика, можно считать 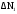= 0. Тогда последние два члена выражения (8) можно переписать так:

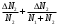(9)

Необходимо обратить внимание на то, что N₂ входит в выражение (7) как в числитель, так и в знаменатель. Знак погрешности 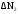нам неизвестен; но он будет один и тот же как в числителе, так и в знаменателе. Допустим, что 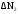, имеет знак плюс; тогда величина вычисленная по формуле (7), из-за присутствия 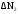в числителе будет получена увеличенной по сравнению с истинным ее значением. Но наличие 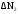в знаменателе с тем же знаком уменьшает значение J. Следовательно, эти погрешности отчасти компенсируются. Математически мы можем учесть это, беря второй член выражения (9) со знаком минус, т.е. надо рассмотреть

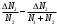(10)

Так как обычно 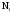, мало по сравнению с 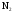, то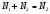



Тогда выражение (10) можно считать равным нулю:



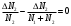
Учтя все эти замечания, для относительной погрешности Е будем иметь более простое выражение:

---

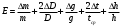
Абсолютные погрешност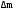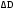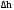и , , и 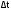определяют, исходя из точности приборов. Вычислив относительную погрешность, находят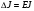



Записывают окончательный результат



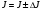
Таблица записи наблюдений

m₁ = г h₁ = см m₂ = г h₂ = см D =

	t1, c	N2	t2, c	N2
1
2
3
4
5
6
7
8
9
10
	t1 =		t2 =

---

Смотрите также файлы

• Виды исполнительного учреждения Отбывания наказания в обычных условиях.docx

• Сборник упражнений по профессиональной подготовке личного состава фпс гпс. Развернутый план занятия.doc

• Контрольная работа по дисциплине пм. В. 03 Выполнение работ по профессии рабочих, должности служащих Инструктор служебного собаководства выполнил студент гр. Пд420.docx

• Мені пірім Сйінбай, Сз сйлемен сиынбай!.doc

• Саба Мектеп.docx