Файл: Лабораторная работа 2 Решение транспортной задачи с помощью Excel Транспортная задача Задача 1.docx

Лабораторная работа № 2

Решение транспортной задачи с помощью Excel
Транспортная задача
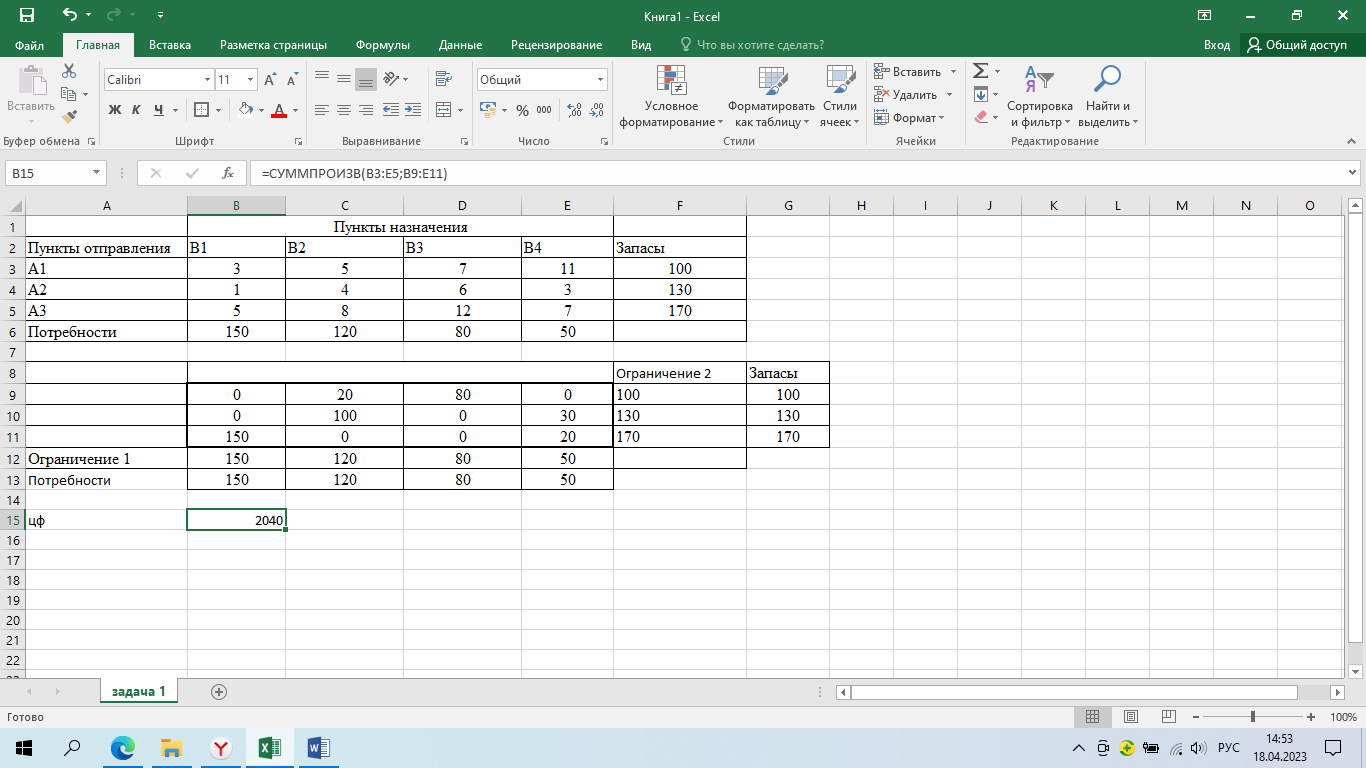
Задача 1.

В городе имеются три домостроительных комбината (ДСК): А1, А2, А3 и строятся четыре микрорайона: В1, В2, В3, В4. Известны ресурсы: А1 – 100, А2 – 130, А3 – 170 и производственные потребности унифицированных изделий микрорайона: В1 – 150, В2 – 120, В3 – 80, В4 – 50. Известны также затраты, связанные с доставкой одного комплекта унифицированных изделий из каждого пункта комплектования в каждый пункт назначения.

	В1	В2	В3	В4
А1	3	5	7	11
А2	1	4	6	3
А3	5	8	12	7

Требуется распределить продукцию ДСК по микрорайонам, чтобы суммарные приведенные затраты, связанные с доставкой всего груза от отправителя к потребителю, были минимальны.

Определили с помощью поиска решений:



Задача 2. Оптимальный план перевозки автомобилей

Два автомобильных завода Р1 и Р2 связаны с тремя дилерами D1, D2 и D3, имеющими два транзитных (перевалочных) центра Т1 и Т2, как показано на рис.1. Заводы Р1 и Р2 производят 1000 и 1200 автомобилей. Заказы дилеров составляют соответственно 800, 900 и 500 автомобилей. Стоимость перевозок одного автомобиля (в сотнях тыс.руб.) показана на рис.1 возле соответствующих дуг.



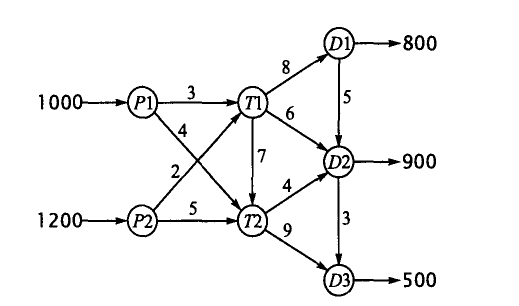
Рис. 1

Указание

Для промежуточных пунктов используйте буфер.


Решение

В данной модели перевозки транзитом осуществляются, помимо прочего, и через некоторые пункты назначения. Пусть пункты, которым соответствуют как входящие, так и выходящие дуги на схеме рис. 1, являются транзитными (пункты Т1, Т2 и D1, D2). Оставшиеся будут либо истинными пунктами отправления (пункты Р1 и Р2), либо истинными пунктами назначения (в данной схеме такой пункт только один – D3).

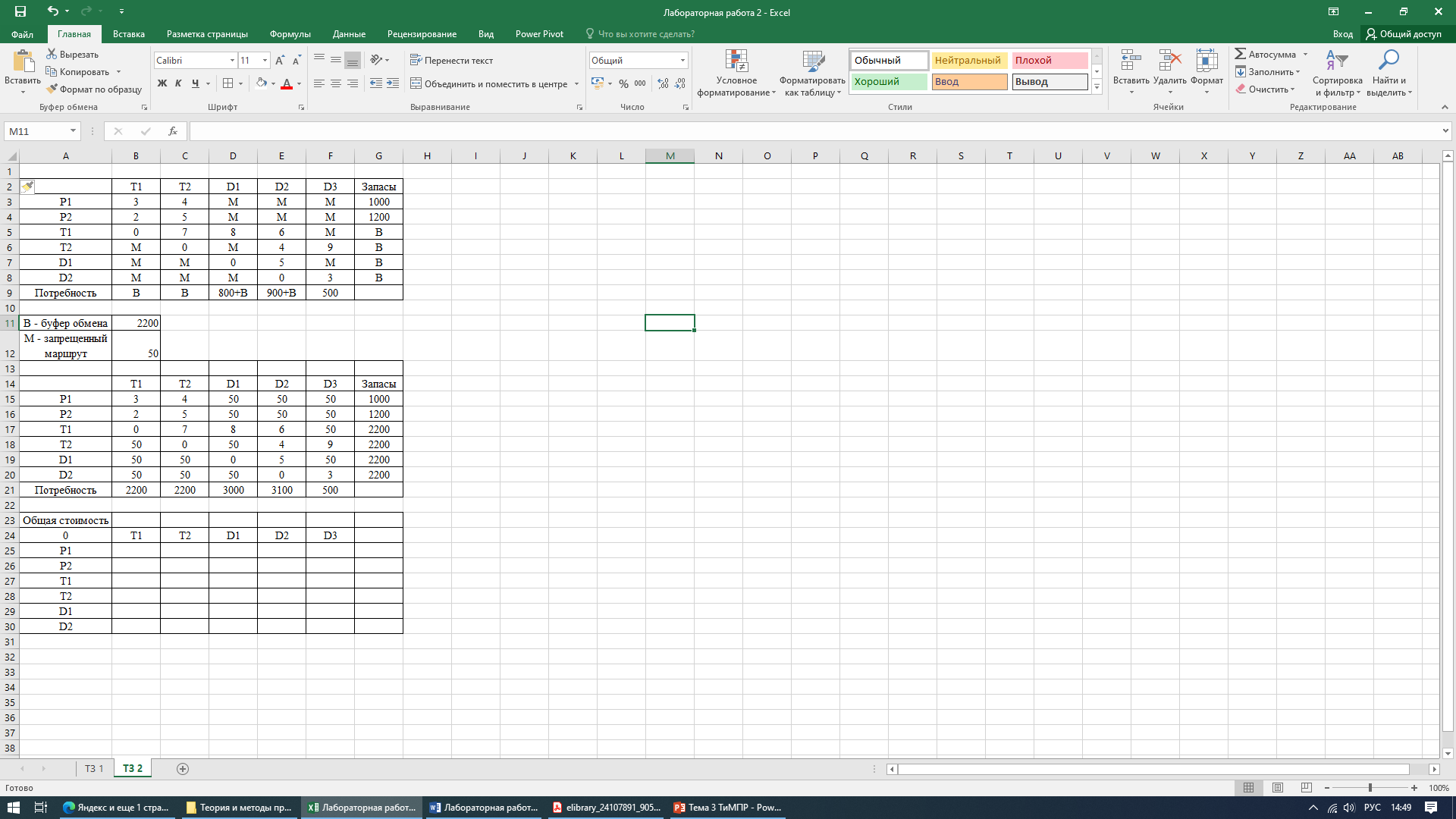
Теперь преобразуем модель задачи управления поставками через транзитные пункты в обычную транспортную модель с шестью пунктами отправления (P1, P2, Т1, Т2, D1 и D2) и пятью пунктами назначения (Т1, Т2, D1, D2 и D3).

Вычисляем объем буфера:
В = 1000 +1200 = 2200 или В = 800 + 900 + 500 + 2200 .
Матрица стоимости поставок для задачи управления поставками через транзитные пункты представлена в таблице.

	T1	T2	D1	D2	D3
Р1	3	4	M	M	M	1000
Р2	2	5	M	M	M	1200
Т1	0	7	8	6	M	B
Т2	M	0	M	4	9	B
D1	M	M	0	5	M	B
D2	M	M	M	0	3	B
	B	B	800+B	900+B	500

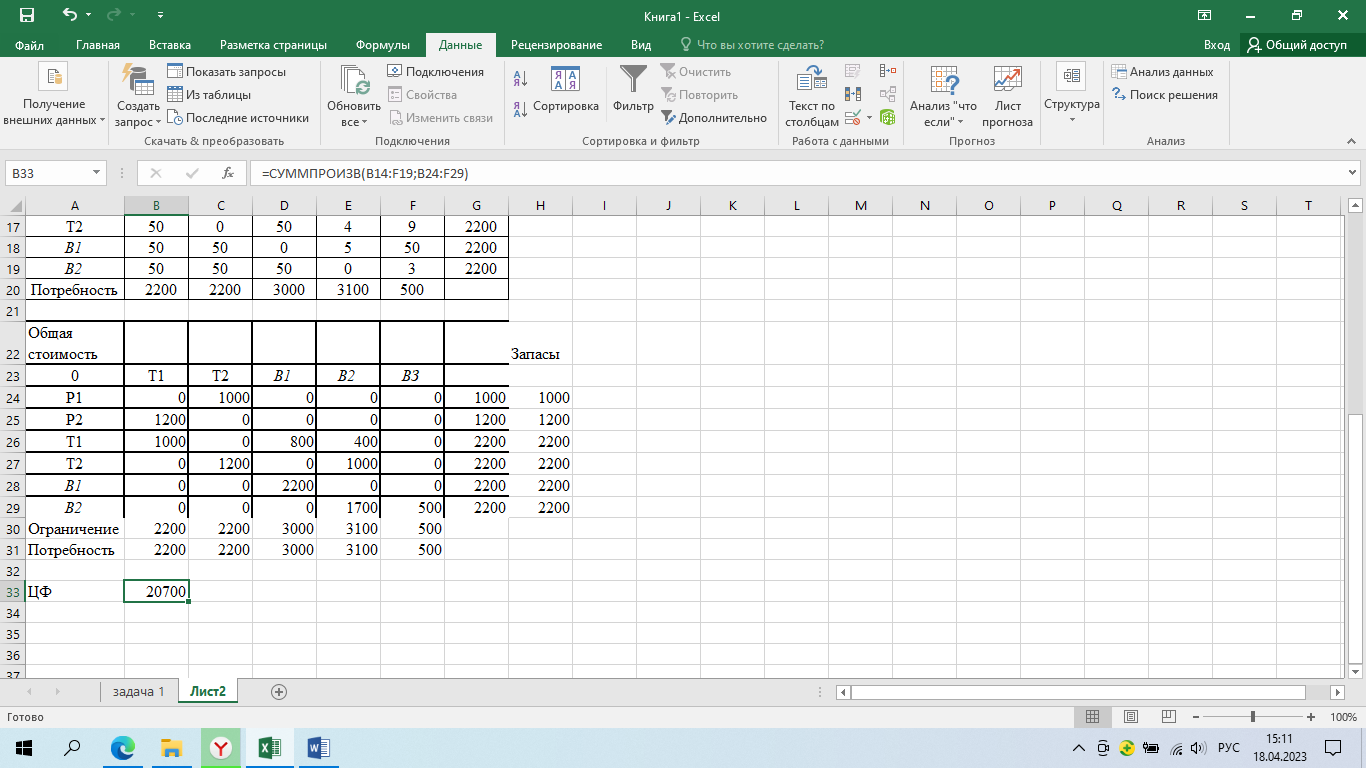
Далее переносим данные в Excel-таблицу и решаем транспортную задачу с помощью функции поиск решения.



Определили с помощью поиска решений:

Задача 3. Оптимальный план перевозки

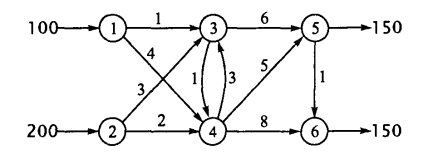
В транспортной сети, показанной на рис., осуществляются перевозки из пунктов 1 и 2 в пункты 5 и 6 через транзитные пункты 3 и 4. Стоимость перевозок показана на этом же рисунке.

Решите транспортную задачу.



Задача 4. Фабрики и магазины
Две фабрики снабжают определенной продукцией три магазина. Объемы производства фабрик равны 200 и 300 единиц продукции, а потребности ма­газинов составляют 100, 200 и 50 единиц продукции. Исследуется возмож­ность перевозок продукции через промежуточные пункты. Основываясь на величинах стоимости перевозок (в д.е.), приведенных в табл., найдите оптимальный план перевозок.

		Фабрики		Магазины
Фабрики		1	2	1	2	3
	1	0	6	7	8	9
	2	6	0	5	4	3
Магазины	1	7	2	0	5	1
	2	1	5	1	0	4
	3	8	9	7	6	0