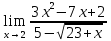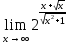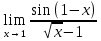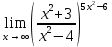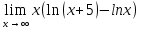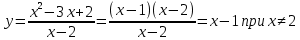Файл: Задание 2 раздел введение в математический анализ задача 1.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Не указан

Дисциплина: Не указана

Добавлен: 04.12.2023

Просмотров: 27

Скачиваний: 1

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.




МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ
федеральное государственное бюджетное образовательное учреждение

высшего образования
«Тольяттинский государственный университет»
Институт машиностроения
(наименование института полностью)
Кафедра /департамент /центр1 Кафедра «Институт машиностроения»

(наименование кафедры/департамента/центра полностью)

Практическое задание №_2__
по дисциплине (учебному курсу) «___Высшая математика 1_____»

(наименование дисциплины (учебного курса)
Вариант 10 (при наличии)


Студент
Лаптев.А.В

(И.О. Фамилия)



Группа
ЭЛбп-2102а



Преподаватель

Липилина Вера Васильевна

(И.О. Фамилия)



Тольятти 2023

Задание 2

РАЗДЕЛ № 4. ВВЕДЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАЛИЗ

Задача 1

Построить графики функций.

а)

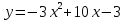
Графиком функции является парабола.

Найдем координаты вершины:



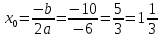
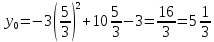
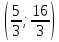– вершина ветви напрвлены в низ.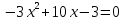





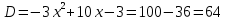
Найдем точки пересечения оси х:







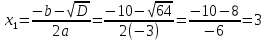
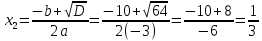
б)

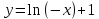
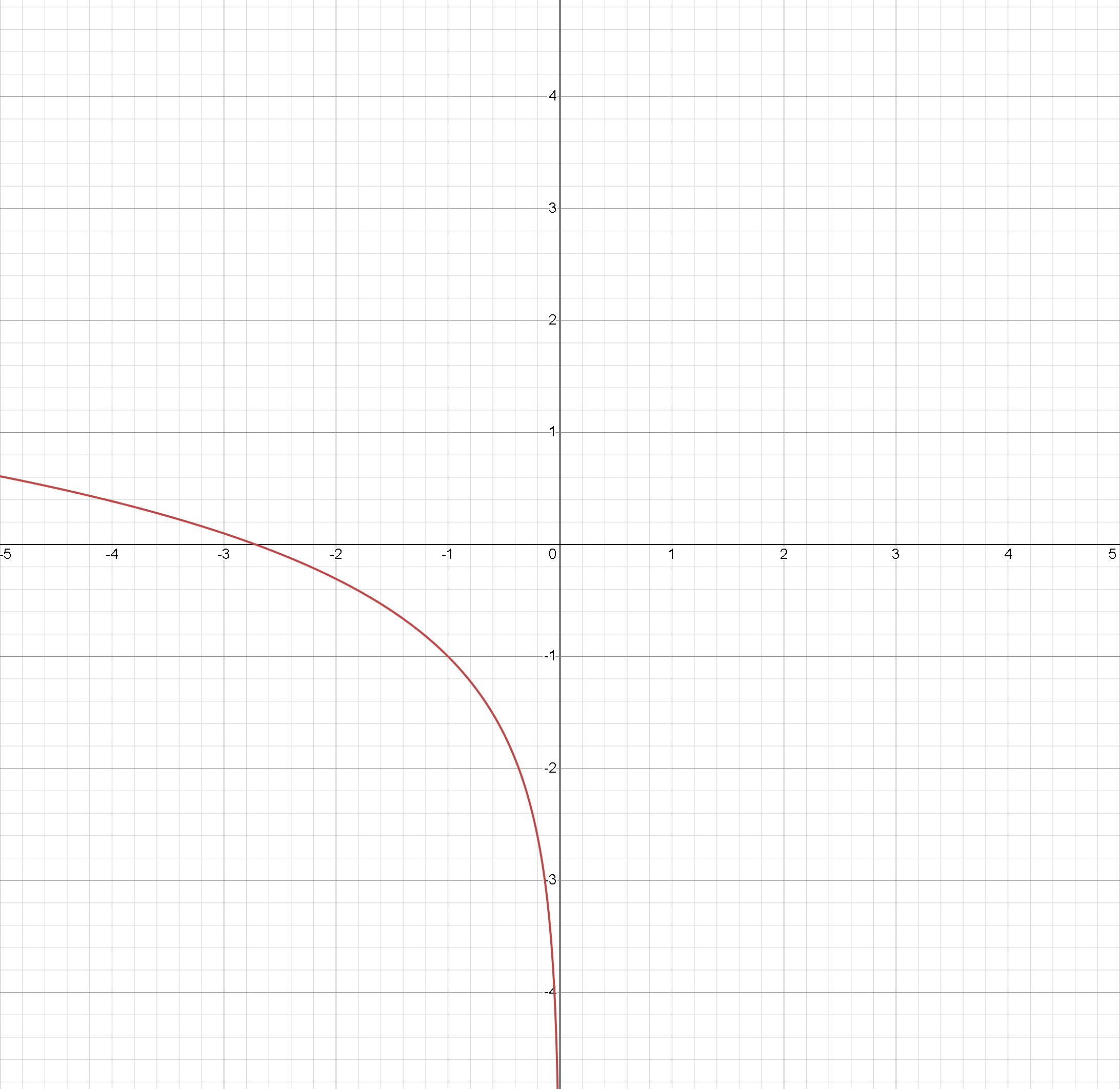
График получен из графика функции ln(-х) со сдвигом на -1 единицу по оси y


в)

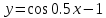
График постороен на основе графика cosx, со смешение по оси у на -1 поэтому график распологаем ниже 0 по оси у, и растяжением сосинусойды по оси х с вершиной 4π вместо 2π.


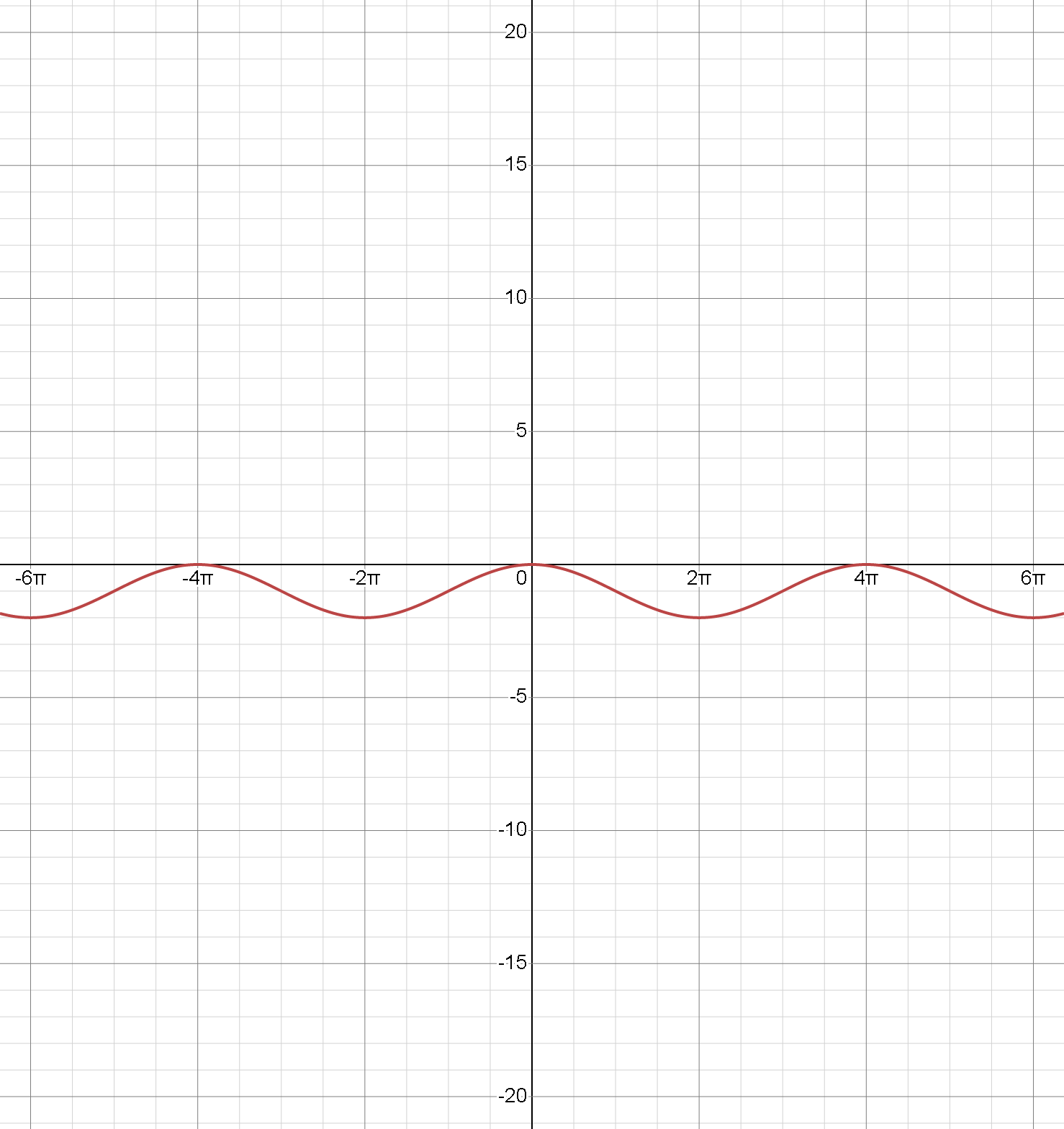
г)





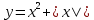
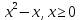
x0=0;

y0=

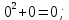
x1=2;

y1=4+2=6;

x2=-2;

y2=4+|-2|=6;


Задача 2

Записать уравнения кривых в полярных координатах и построить их.





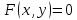
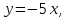
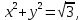
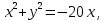
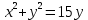
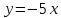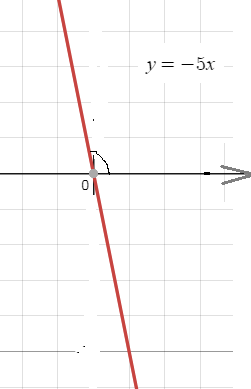
  1. – прямая в полярных координатах

r sinφ=-5 r cosφ ⇒ sinφ=-5 cosφ ⇒ tgφ=-5

Это уравнение прямой в полярных координатах



б) 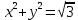– уравнение окружности с центром (0;0) и

радиусом r=









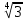
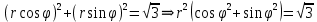
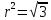
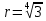
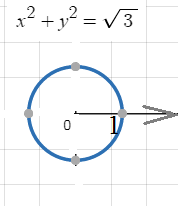
в)



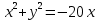
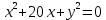
Выделяем полный квадрат



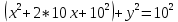
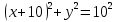- уравнение окружности с центром (–10;0) и

радиусом r=10







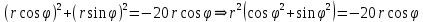
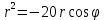
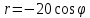
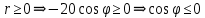- график расположен в 2 и 3 четвертях.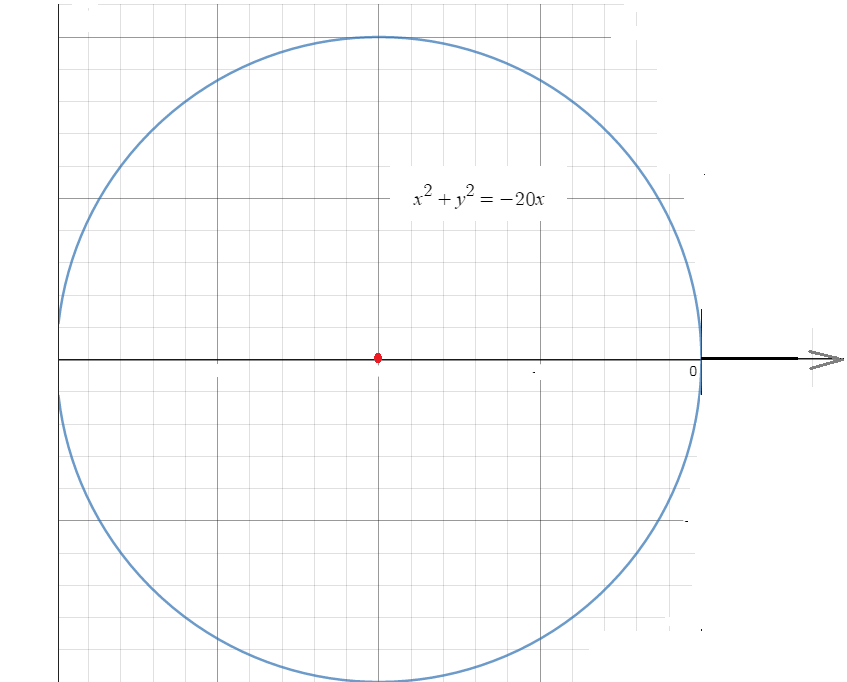



г)



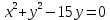
Выделяем полный квадрат

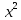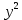( +( –2·7,5y+ )=

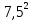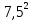
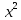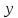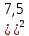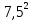+( – = – уравнение окружности с центром (0;7,5) и

радиусом R=7,5







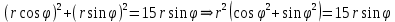
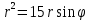
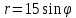
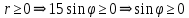- график расположен в 1 и 2 четвертях.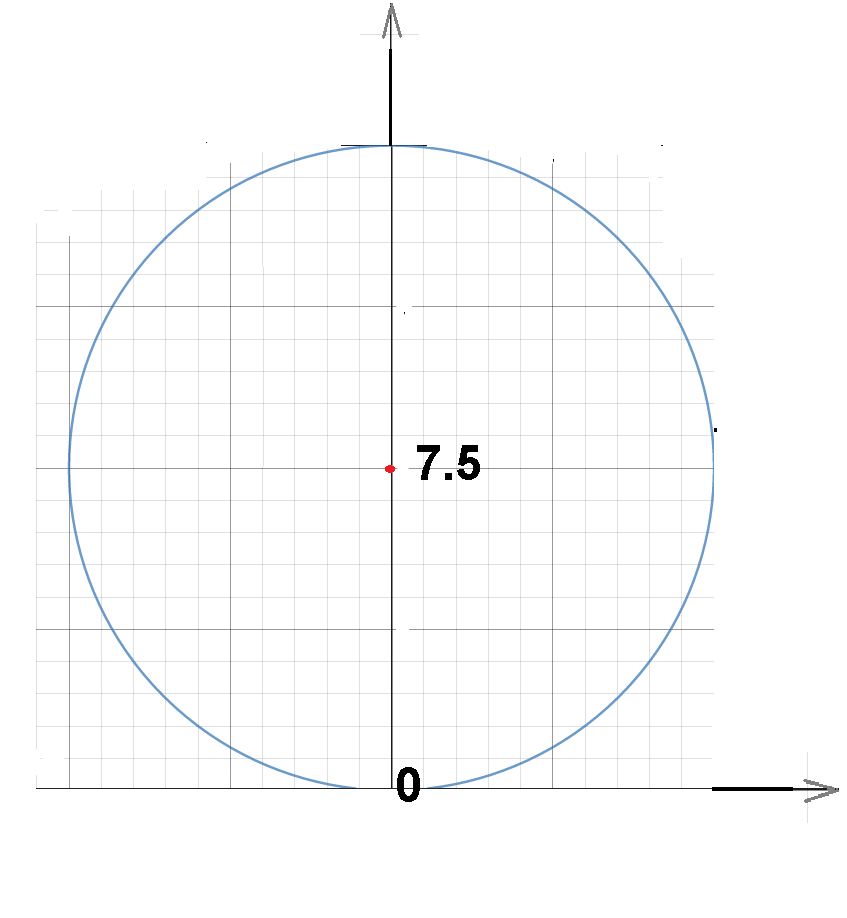



Задача 3

Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.







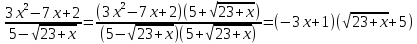
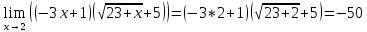
Ответ: -50.



Преобразуем:


































=







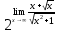
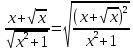
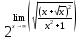
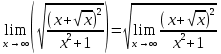
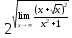
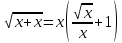
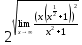
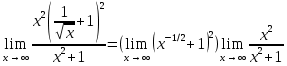
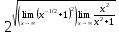
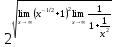
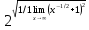
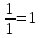
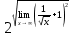
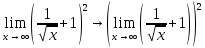
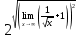
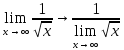
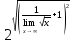
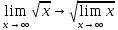
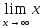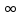
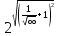
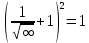
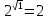
Ответ: 2.




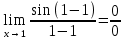- неопределенность.

Подстановка

x=t+1 t=x-1 x 1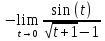













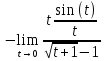
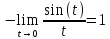
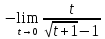
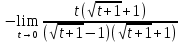
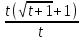
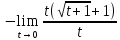
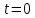
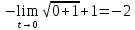
Ответ: -2.










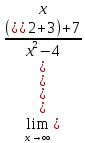
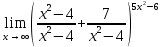
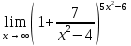
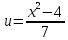
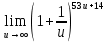
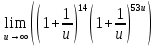
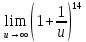
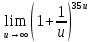
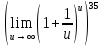
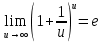тогда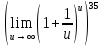
=

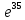
Ответ:





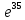
Применяем формулу





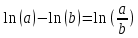
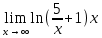
Преобразование





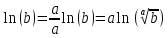
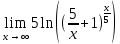
Второй замечательный предел




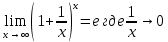
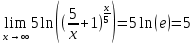
Ответ: 5.
Задача 4

Исследовать на непрерывность функции, найти точки разрыва и

определить их тип. Построить схематические графики функций.


Смотрите также файлы