Файл: Практикум по курсу " Теория управления" Вариант 21 Выполнил Ст гр. Преподаватель спбгэту лэти.doc

…

9. Модель замкнутой СУ задана в задаче 2. В каких рассмотренных выше задачах фигурирует характеристический полином системы?

В задачах № … , … , в выражениях … (указать, где представлен).
10. Модель СУ задана в вопросе 2. Провести анализ устойчивости этой системы. Использовать алгебраический критерий Гурвица.

1: система устойчива,

2: система нейтральна (находится на нейтральной границе устойчивости),

3: система находится на колебательной границе устойчивости,

4: система неустойчива.

(Привести необходимые вычисления и обосновать ответ).

11. Модель СУ задана в вопросе 2. Усиление в контуре обратной связи K=K_1K_2K_3K₄. Есть возможность изменять (варьировать) параметр K₁. K_{кр } “критический” коэффициент усиления контура, при котором система находится на колебательной границе устойчивости. Чему равно значение K=K_кр ? Использовать алгебраический критерий Гурвица.

K_кр=….

(Привести необходимые вычисления и обосновать ответ).

На рис.5 приведены графики процесса в системе при K=K_кр.


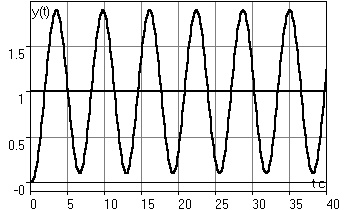
Рис. 5

Вывод о совпадении результата “ручного” и автоматизированного расчетов:

…

12. Модель СУ задана в задаче 2. Изменяем оператор звена 4: W₄(s)=K₃/(T₂s+1). Полагаем T_2=0. В результате получаем W₄(s)=K₃.

Определить область устойчивости для коэффициента усиления контура – интервал значений (K_minKK_max

---

), при котором система устойчива.

1: (0K1.25); 2: (0K100); 3: (0K); 4: (K).

(Обосновать ответ).

13. Модель замкнутой СУ задана в вопросе 2.

Построить с использованием программы CLASSiC амплитудную L_р() и фазовую _р() логарифмические частотные характеристики разомкнутой системы.

Скопировать график в данный отчет. На этом же графике с помощью средств рисования WORD построить асимптотическую ЛАХ, обозначить графики и показать запас по фазе (если система устойчива).

Примечание. Для указанных построений могут быть использованы элементы рис.6, приведенного в качестве образца; для этого рисунок следует “Разгруппировать”.

Н
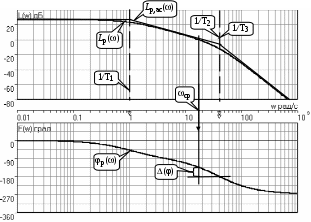
а рис.6 приведены результаты расчета и требуемые построения.

Рис. 6

Результат автоматизированного расчета:

Частота среза: 0.6823 рад/с

Запас по фазе: 21.3864 град

Частота пи: 1.0000 рад/с

Запас по модулю: 6.0206 дБ

Примечание. Частотные показатели качества в программе CLASSiC выводятся из окна “Характеристики”, команды меню “Графики”Показатели качества”. При этом должно быть активизировано окно “Частотные характеристики”.

1
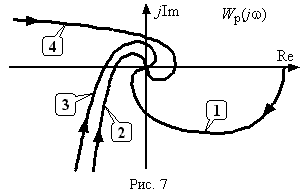
3. На рис.7 построены качественно амплитудно-фазовые частотные характеристики W_P(j) разных разомкнутых СУ.

Которая из этих характеристик соответствует системе, заданной в задаче 2 ?

1; 2; 3; 4.

14. Модель СУ задана в вопросе 2. Изменяем оператор звена 5. Полагаем W₅(s)=K₄.

Которая из частотных характеристик, изображенных на рис.7, соответствует такой системе?

1; 2; 3; 4.
1
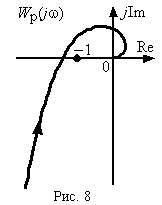
5.

---

На рис.8 построена качественно амплитудно-фазовая частотная характеристика W_P(j) некоторой разомкнутой СУ.

Проанализировать устойчивость системы в замкнутом состоянии. Использовать критерий Найквиста.

1: система устойчива,

2: система нейтральна (находится на нейтральной границе устойчивости),

3:система находится на колебательной границе устойчивости,

4: система неустойчива.

(Обосновать ответ).

---