Задание 2
112121111

4	y 5x2  26x 5, y  ln3x  2, y  sin 2x  2, y  x x.
5	y  2x2 3x 2, y  ln( 2  2x), y cos 2x, y  x x 1.
6	y  3x2 8x 3, y  ln2x  3, y sin 2x, y  x  2 x 1.
7	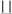x  4x2 15x 4, y  ln x  3, y  cos 1, y  2 . 2 x
8	y  5x2  24x 5, y  ln( 3x )1, y  sin0,5x  2, y  e x .
9	y 2x2 3x  2, y  ln( x 4 ), y  sin0,5x  1, y  ln x.
10	x y 3x2 8x 3, y  ln( x ) 2, y  cos  2, y  sin x. 2
11	x y  6x2 5x 1, y ln x  2, y  sin , y  e x2 . 2
12	x y 2x2 7x 3, y ln x 1, y  cos , y  ln x 1. 2

---

19	3x 2x2 7x 3, y  cos , y   3 , y  ln x 1. 2 x 1
20	x y  6x2 5x 1, y sin , y ex 1, y  e x2 . 2

Задача 2 Номер варианта задачи определяется с помощью таблицы по первой букве отчества студента. Таблица. Выбор номера варианта

Буква	А	Б	В	Г	Д	Е, Ё	Ж, З	И	К	Л
№ вар.	1	2	3	4	5	6	7	8	9	10
Буква	М	Н, Ю	О, Я	П	Р, Ч	С, Ш	Т, Щ	У	Ф, Э	Х, Ц
№ вар.	11	12	13	14	15	16	17	18	19	20

Записать уравнения кривых в полярных координатах и построить их.

Номер вар.	F( x,y )  0
1	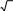y 5x, x2  y2  3, x2  y2 20x, x2  y2  15y.
2	x 4y, x2  y2  200, x2  y2  x, x2  y2 14y.
3	x  2y, x2  y2  169, x2  y2 12x, x2  y2  0,8y.
4	x  y  8, x2  y2  121, x2  y2 14x, x2  y2  0,6y.
5	x x  y  1, x2  y2  125, x2  y2  , x2  y2  12y. 4
6	x  3,5, x2  y2  100, x2  y2 9x, x2  y2  10y.
7	x , x2  y2  16, x2  y2  3y, x2  y2  3y.
8	x  , x2  y2  81, x2  y2  12x, x2  y2 10y. 4
9	x  , x2  y2  64, x2  y2 8x, x2  y2  0,4y. 2
10	y 3, x2  y2  49, x2  y2 5x, x2  y2  6y.
11	x 3, x2  y2  36, x2  y2  5x, x2  y2 6y.
12	y  , x2  y2  25, x2  y2 4x, x2  y2  5y.
13	x 1, x2  y2  9, x2  y2  3x, x2  y2 4y.
Номер вар.	F( x,y )  0
14	y  0,5, x2  y2  12, x2  y2  x, x2  y2 y.
15	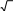x  0,5, x2  y2  3, x2  y2 x, x2  y2  12y.
16	x  1, x2  y2  3, x2  y2  4x, x2  y2  5y.
17	y  3, x2  y2  4, x2  y2  4x, x2  y2  5y.
18	x  3, x2  y2  5, x2  y2  6x, x2  y2 7y.
19	y  5, x2  y2  6, x2  y2 7x, x2  y2  8y.
20	x  5, x2  y2 7, x2  y2  8x, x2  y2  9y.

---

Задача 3 Номер варианта задачи определяется с помощью таблицы по первой букве фамилии студента.

№	Пределы
1	5x2 1) lim 11x  2; 2) lim( 1 x)(8 1 x3 ); 3) lim sin2( x 10) ; x2 7  x 3 x 5x 8 x 10 x2 36 8 4) lim x14x1; 5) lim x(ln( x 10) ln x ). x x3 x

Таблица. Выбор номера варианта

Буква	А	Б	В	Г	Д	Е, Ё	Ж, З	И	К	Л
№ вар.	1	2	3	4	5	6	7	8	9	10
Буква	М	Н, Ю	О, Я	П	Р, Ч	С, Ш	Т, Щ	У	Ф, Э	Х, Ц
№ вар.	11	12	13	14	15	16	17	18	19	20

Вычислить пределы функций, не пользуясь средствами дифференциального исчисления.

---

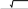
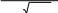
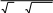
Задача 4 Номер варианта задачи определяется с помощью таблицы по первой букве имени студента. Таблица. Выбор номера варианта

Буква	А	Б	В	Г	Д	Е, Ё	Ж, З	И	К	Л
№ вар.	1	2	3	4	5	6	7	8	9	10
Буква	М	Н, Ю	О, Я	П	Р, Ч	С, Ш	Т, Щ	У	Ф, Э	Х, Ц
№ вар.	11	12	13	14	15	16	17	18	19	20

Исследовать на непрерывность функции, найти точки разрыва и определить их тип. Построить схематические графики функций.

№	Функции
1	x2,  x 2; x2 3x2 x  4  1) y  ; 2) y  ; 3) y  x  2, 0  x  0; x2 x  4 3x, 0  x . 
2	x2 10x  9; 2) y  x  0,8 22xx35,, 0xx2;0; 1) y  ; 3) y  x 9 x  0,8 7, 2  x . 
3	 x2 1,  x  0; x 1) y  2 7x 12; 2) y  2x  5 ; 3) y x 1, 0  x  2; x 4 2x  5 4, 2  x . 
4	x2 7x 6 x  2  x2,  x 2; 1) y  ; 2) y  ; 3) y 4x  4,  2  x  0; x 1 x  2 5, 0  x . 
5	 x2  2,  x 1; x 1) y  2 4x  3; 2) y  x  6 ; 3) y 3x  2, 1 x  0; x 3 x  6 2, 0  x . 
6	 x2,  x  0; x 1) y  2 8x 12; 2) y  x  3 ; 3) y 2x 1, 0  x 1; x  2 x  3 3, 1 x . 

---

№	Функции
7	x x  5 3x 1,  x  0; 1) y  2 7x 10; 2) y  ; 3) y x2 1, 0  x  1; x  2 x  5 2x, 1 x . 
8	x2 4x  3 x 6 22x 12,, 1xx1;1; 1) y  ; 2) y  ; 3) y x  x 1 x 6 3, 1 x . 
9	x2 6x  8 x 7 4x 1,2, 0xx1;0; 1) y  ; 2) y  ; 3) y ( x 1) x 4 x 7 4, 1 x . 
10	x2 1,  x  0; x x 8 1) y  2 5x 6 ; 2) y   ; 3) y x, 0  x 1; x 6 x  8 x 1, 1 x . 
11	 x2  2,  x  0; 1) y  2 6x  8; 2) y   9 ; 3) y x  2, 0  x  2; x x x  4 x  9 5, 2  x . 
12	 x2,  x  0; x 1) y  2  8x 12; 2) y  x 10 ; 3) y x, 0  x  3; x 6 x 10 2x 1, 3 x . 
13	1 x2,  x 1; 1) y  2 8x 12; 2) y  x 1. ; 3) y x 1, 1 x  4; x 2 x 6 2x 1 x 1, 4  x . 
14	3x  5,  x  0; x 1) y  2 5x 6 ; 2) y  3x 1. ; 3) y x  52, 0  x  5; x 3 3x 1 1, 5  x . 
15	2x 1,  x  0; x 1) y  2 10x 16 ; 2) y  x  3 ; 3) y  x 12, 0  x 1; x  2 x  3 2, 1 x . 
16	x2  5x 6 x  3 4x  5,  x  0; 1) y  ; 2) y  ; 3) y  5, 0  x  2; x  2 x  3 x 1, 2  x . 
№	Функции
17	4x 1,  x  0; x 1) y  2  5x 6 ; 2) y  4x  1 ; 3) y x2 1, 0  x 1; x  2 4x  1 0, 1 x . 
18	2x  3,  x  0; x 1) y  2 4x 5; 2) y  5x 1 ; 3) y x  32, 0  x 1; x 1 5x 1 4, 1 x . 
19	2x  2,  x 1; x 1) y  2 8x 15; 2) y  6x  1 ; 3) y x2 1, 1 x 1; x 3 6x  1 4, 1 x . 
20	20,  x  0; 1) y   8x  ; 2) y  2x  3 ; 3) y  2x, 0  x  3; x 15 x  5 2x  3 5x 1, 3 x . 

---

Смотрите также файлы

• Обучающийся Грядовкина Юлия Николаевна Преподаватель Чащинова Анна Вадимовна Практическое занятие.rtf

• Феномен работающего студента.pptx

• Привет меня зовут Катя я родилась в городе Булаево. Изначально я думала что город Булаево появилось так, однажды приехал человек у которого фамилия Булаев, но тут не так всё просто.docx

• Синдром слабости синусового узла.doc

• Литература Гаврина.docx