Файл: Основные понятия комплексных чисел Определение комплексного числа в алгебраической форме, действия над ними.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 22
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Основные понятия комплексных чисел
Определение комплексного числа в алгебраической форме, действия над ними.
Мнимые числа, которыми мы дополняем действительные числа, записываются в виде bi, где i – мнимая единица, причем i 2 = -1.
Исходя из этого, получим следующее определение комплексного числа.
Комплексным числом называется выражение вида a + bi, где a и b - действительные числа. При этом выполняются условия:
а) Два комплексных числа a1 + b1i и a2 + b2i равны тогда и только тогда, когда a1=a2, b1=b2.
б) Сложение комплексных чисел определяется правилом:
(a1 + b1i) + (a2 + b2i) = (a1 + a2) + (b1 + b2) i.
в) Умножение комплексных чисел определяется правилом:
(a1 + b1i) (a2 + b2i) = (a1a2 - b1b2) + (a1b2 - a2b1) i.
Запись комплексного числа в виде a + bi называют алгебраической формой комплексного числа, где а – действительная часть, bi – мнимая часть, причем b – действительное число.
Комплексное число a + bi считается равным нулю, если его действительная и мнимая части равны нулю: a = b = 0
Комплексное число a + bi при b = 0 считается совпадающим с действительным числом a: a + 0i = a.
Комплексное число
a + bi при a = 0 называется чисто мнимым и обозначается bi: 0 + bi = bi.
Два комплексных числа z = a + bi и
= a – bi, отличающиеся лишь знаком мнимой части, называются сопряженными.Над комплексными числами в алгебраической форме можно выполнять следующие действия.
1) Сложение. Суммой комплексных чисел z1 = a1 + b1 i и z2 = a2 + b2i называется комплексное число z, действительная часть которого равна сумме действительных частей z1 и z2, а мнимая часть - сумме мнимых частей чисел z1 и z2, то есть z = (a1 + a2) + (b1 + b2) i. Числа z1 и z2 называются слагаемыми.
Сложение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z1 + z2 = z2 + z1.
2º. Ассоциативность: (z1 + z2) + z3 = z1 + (z2 + z3).
3º. Комплексное число – a – bi называется противоположным комплексному числу z = a + bi. Комплексное число, противоположное комплексному числу z, обозначается -z. Сумма комплексных чисел z и -z равна нулю: z + (-z) = 0
2) Вычитание. Вычесть из комплексного числа z1 комплексное число z2, значит найти такое комплексное число z, что z + z2 =z1. Разность комплексных чисел существует и притом единственная.
3) Умножение. Произведением комплексных чисел
z1=a1+ b1 i и z2=a2+b2i называется комплексное число z, определяемое равенством:
z = (a1 a2 – b1b2) + (a1b2 + a2b1) i. Числа z1 и z2 называются сомножителями.
Умножение комплексных чисел обладает следующими свойствами:
1º. Коммутативность: z1z2 = z2 z1.
2º. Ассоциативность: (z1z2)z3 = z1 (z2z3)
3º. Дистрибутивность умножения относительно сложения:
(z1 + z2) z3 = z1z3 + z2z3.
4º. z ·
= (a + bi) (a – bi) = a2 + b2 - действительное число.На практике умножение комплексных чисел производят по правилу умножения суммы на сумму и выделения действительной и мнимой части.
4) Деление. Разделить комплексное число z1 на комплексное число z2, значит найти такое комплексное число z, что z · z2 = z1. Частное комплексных чисел существует и единственно, если z2 ≠ 0 + 0i.
5) а) Возведение в целую положительную степень. Чтобы возвести число i в целую положительную степень, надо показатель степени разделить на 4 и возвести i в степень, показатель которой равен остатку от деления.
б) Возведение комплексного числа в целую положительную степень производится по правилу возведения двучлена в соответствующую степень, так как оно представляет собой частный случай умножения одинаковых комплексных сомножителей.
С помощью комплексных чисел можно решать квадратные уравнения, у которых отрицательный дискриминант.
Геометрическое изображение комплексных чисел.
Модуль и аргументы комплексного числа.
Любое комплексное число (кроме нуля) z=a+bi можно записать в тригонометрической форме:
z=|z|∙(cosφ+isinφ),
где |z| – это модуль комплексного числа, а φ – аргумент комплексного числа.
Изобразим на комплексной плоскости число z=a+bi . Для определённости и простоты объяснений расположим его в первой координатной четверти, т.е. считаем, что a>0, b>0 :
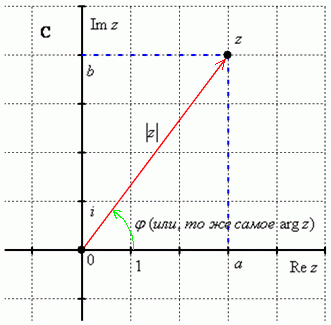
Модулем комплексного числа z называется расстояние от начала координат до соответствующей точки комплексной плоскости. Попросту говоря, модуль – это длина радиус-вектора, который на чертеже обозначен красным цветом.
Модуль комплексного числа z стандартно обозначают: |z| или r.
По теореме Пифагора легко вывести формулу для нахождения модуля комплексного числа:
. Данная формула справедлива для любых значений a и b.
Аргументом комплексного числа z называется угол φ между положительной полуосью действительной оси Re z и радиус-вектором, проведенным из начала координат к соответствующей точке. Аргумент не определён для единственного числа: z=0.
Аргумент комплексного числа z стандартно обозначают: φ или arg z.
Из геометрических соображений получается следующая формула для нахождения аргумента:
Данная формула работает только в правой полуплоскости! Если комплексное число располагается не в 1-ой и не 4-ой координатной четверти, то формула будет немного другой.
Формулы для нахождения
в зависимости от а и b:
1.
2.
3.
4.
5.
6.
7.
8.
