Файл: Исследование генератора шума afg3021 и влияния шума на различные сигналы.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 54
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Цель работы: Исследование генератора шума AFG3021 и влияния шума на различные сигналы.
-
Теоретические сведения.
-
Псевдослучайные сигналы
Псевдослучайный сигнал – это такой сигнал, у которого при неограниченном росте периода за счет усложнения формы характеристики стремятся к характеристикам близкого к нему по структуре случайного сигнала.
Мгновенные значения псевдослучайных сигналов (ПСС) можно, хотя бы в принципе, определить в любой наперед заданный момент времени. Для случайных сигналов это сделать нельзя. У ПСС любые требуемы характеристики можно получить, использовав его реализацию длиной в один период. Для случайных сигналов требуется реализация бесконечной суммы.
Если анализировать ПСС, то окажется, что они имеют линейчатый спектр (за бесконечной длительный интервал времени.) Но реально при конечной длительности спектр будет сплошным.
Для сигналов конечной длительности оказывается полезным понятие
«текущий спектр».
Под текущим спектром понимают функцию, определяемую формулой:
t
F(t,) (t)e jtdt. (1)
0
Смысл этой формулы состоит в том, что некоторая вещественная функция (t) , о которой можно сказать только, что она удовлетворяет условиям Дирихле и абсолютно интегрируема в бесконечных пределах, отображается в
частотной области функцией
F(t,). Если (t)
функция периодическая,
F(t,) в
пределе t станет линейчатой, если
(t)
апериодическая функция, спектр будет сплошным.
Периодические сигналы при конечном верхнем пределе будут занимать
промежуточное значение – их спектр будет сплошным, но
F(t,)
будет
представлять собой функцию, у которой по мере роста времени t(рассматриваемого в качестве примера) будут появляться максимумы. В зависимости от того, сколько периодов процесса успевает пройти за время
наблюдения, процесс можно назвать коротким или длинным. Чем длиннее в этом смысле наблюдательный процесс, тем ярче в его текущем спектре проявляются максимумы у основной частоты повторения и у гармоник.
Если наблюдается только отрезок процесса, соизмеримый с периодом, спектр не успевает сгруппироваться и остается, как и у случайного сигнала, сплошным. Однако, если ПСС каждый раз начинается с одного и того же
значения
(t 0 ), то в момент
t tk
он же однозначно определен и в этом
смысле является регулярным.
Если рассматривать «короткие» реализации ПСС (равные или меньше его периода), нет возможности определить, являются ли эти реализации отрезками регулярных или случайных процессов.
От ПСС обычно требуется, чтобы он имел период достаточно большой по
сравнению с величиной, обратной эффективной ширине его спектра
fПСС.
Указанное условие оказывается удовлетворительным, если форма сигнала будет сплошной, т.е. мгновенное значение непрерывно или дискретных точках меняются достаточно быстро.
-
Способы получения псевдослучайных двоичных сигналов.
Псевдослучайная последовательность максимальной длины приведена на рисунке 1.
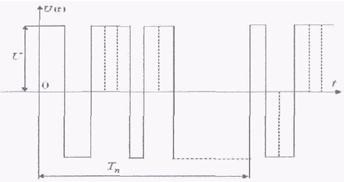
Рисунок 1 - Псевдослучайная последовательность максимальной длины
Смена знаков напряжения производится в определенном порядке много раз за период.
При выполнении определенных условий эти сигналы могут заменять и весьма часто заменяют «бинарный шум» (последовательности случайных одноразрядных чисел).
Наибольшее применение в качестве сигналов, призванных заменить
«бинарный шум», нашли так называемые линейные последовательности максимальной длины (М-последовательности). Их получают с помощью генераторов, используемых в качестве основных элементов N-каскадные регистры сдвига и сумматоры по модулю 2.
Схема генератора М-последовательностей приведена на рисунке 2.
Tn 127 .
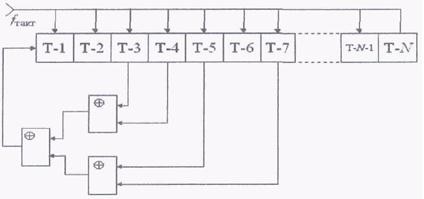
Рисунок 2 – Схема генератора 127-последовательностей
N триггеров имеют общую шину питания, управляющими импульсами, и соединены по схеме регистра сдвига. Достоинства схемы: фиксированная амплитуда, легко и в широком диапазоне регулируемая ширина спектра сигнала, возможность получать сдвинутые по шкале времени сигналы.
Сигналы с единичных выходов определенных триггеров суммируются в
сумматоре по может иметь
mod 2
n 2N
и подаются на вход первого триггера. Схема из Nтриггеров различных состояний. Но одно состояние (когда во всех
триггерах нули) использовать нельзя, так как в таком случае его поступления генерация прекратиться. Генератор после этого может генерировать только нули. Поэтому период повторения, именуемый максимальным, будет
определяться как Tn T(2 1) .
N
Рассмотрим работу схемы. Допустим сначала, что в регистре сдвига зафиксирована в момент включения некоторая комбинация нулей и единиц, а цепь обратной связи, включенная через сумматор по модулю 2, разорвана. Первый тактовый импульс произведет перемещение содержимого триггеров на 1 такт вправо. После его прохождения в первом триггере будет зафиксирован логический «0», в i-1-м триггере – логическая «1» или логический «0», в зависимости от того, что было зафиксировано в i+1-м триггере. После прохождения N-го тактового импульса во всех триггерах будут зафиксированы логические нули, а с выхода N-го триггера пройдет зафиксированная в регистре сдвига комбинация логических «0» и «1».
При включении цепи обратной связи действуют сумматоры по модулю 2.
В этом случае при сдвиге информации в 1-м разряде записывается число Xi,
зафиксированное в предыдущем такте в сумматоре по модулю 2, во 2-й разряд -
Xi1 , в 3-й разряд -
Xi2
и т.д.
Наиболее важным для практики является корреляционные свойства М-последовательности. Автокорреляционные функции, сделанные по случайному заданному закону выборок их М-последовательностей и последовательности, представляющие собой «бинарный шум», будут отличаться друг от друга смещением по оси ординат на величину
R()
U2
2N1
. (2)
Это связно с тем, что в ПСС отсутствуют последовательности вида 000-0 и, благодаря этому, математическое ожидание не равно нулю.
Функция автокорреляции периодической последовательности, рассматриваемой на бесконечном интервале времени, будет периодической функцией времени. Ее можно получить, сдвигая последовательности символов
одного периода
T T(2N1)
на время , вычисляя среднее значение
n
произведения исходной и сдвинутой последовательностей. Очевидно, что при
0
получим
U2 . Далее значения функции автокорреляции с ростом будут
падать до 0 в пределах от 0
до T. При T
функция автокорреляции М-
последовательностей будет представлять собой ломаную линию, изменяющую
наклон в точках
kT, где
k 0;1;2;3;...
Корреляционная функция
последовательности максимальной длины приведена на рисунке 3.
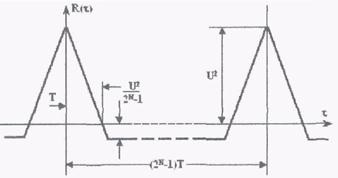
Рисунок 3 – Корреляционная функция последовательности максимальной длины
Спектральная плотность М-последовательности является линейчатой и имеет с характерной огибающей. На рисунке 4. изображена спектральная плотность М-последовательности, приведенная к амплитуде 1-й гармоники.
G0
G00
2
. (3)
G(2 N1)T
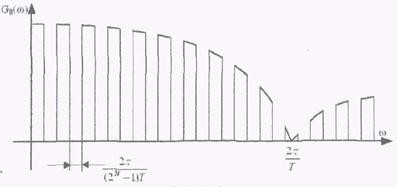
Рисунок 4 - Спектральная плотность M-последовательности
Первый раз она достигает нуля на частоте работы тактового генератора
F 1 . Следовательно, ширина спектра определяется длительностью
T T
n
отдельного символа и не зависит от тактового периода генератора T T(2N1) .