Министерство образования и науки Республики Казахстан

Восточно-Казахстанский государственный технический университет ИМ. Д.М. СЕРИКБАЕВА

А.А. Жаксылыкова
МАТЕМАТИЧЕСКИЙ МАЯТНИК

Методические указания к лабораторной работе №3.01

Усть-Каменогорск, 2004

УДК 530
Жаксылыкова А.А. Математический маятник. Методические указания к лабораторной работе №3.01 / ВКГТУ. – Усть-Каменогорск, 2004. – с.12.


Приведена краткая теория гармонических колебаний в соответствии с программой курса физики для технических университетов. Даны методика исследования законов колебаний математического маятника, описание лабораторной установки, порядок выполнения работы и обработки результатов эксперимента.

Утверждены методическим советом Механико-технологического института

Протокол № ___ от ________ 2004


 Восточно-Казахстанский государственный технический университет имени Д.М. Серикбаева, 2004
СОДЕРЖАНИЕ

стр.

1. Цель работы 4

2. Условные обозначения 4

3. Теоретические сведения 4

4. Приборы и принадлежности 7

5. Описание установки и метода измерений 7

6. Порядок выполнения работы и обработки результатов

измерений 9

7. Контрольные вопросы 11

8. Литература 12


ЛАБОРАТОРНАЯ РАБОТА №3.01

МАТЕМАТИЧЕСКИЙ МАЯТНИК
1.Цель работы: изучение законов колебания математического маятника и определение ускорения свободного падения.

2. Условные обозначения:

-параметр, характеризующий отклонение системы от положения равновесия;

- амплитуда колебаний, м;

- фаза колебаний, рад;

- начальная фаза колебаний, рад;

- циклическая частота, рад/с;

g- ускорение свободного падения, м/с²

- длина математического маятника, м;

---

- период колебаний, с;

- число колебаний.
3 Теоретические сведения

3.1 Основные понятия
Колебательным движением называются процессы, отличающиеся той или иной степенью повторяемости во времени. Колебания называются периодическими, если параметры, характеризующие состояние системы, повторяются через определенный промежуток времени:
, (1)
где - период колебаний, то есть наименьший промежуток времени, через который повторяется состояние системы, или время одного полного колебания; - периодическая функция времени, характеризующая состояние системы.

Наиболее важной разновидностью периодических колебаний являются гармонические колебания. Это колебания, происходящие по закону синуса или косинуса:
(2)

Гармонические колебания совершаются под действием упругой или квазиупругой силы. Упругими называют силы пропорциональные смещению и направленные к положению равновесия, то есть подчиняющееся закону Гука:

, (3)
где - коэффициент упругости. Квазиупругими являются силы неупругие по своей природе, но действующие так же, как и упругие.

В зависимости от характера внешних воздействий колебания бывают свободные и вынужденные. Свободными являются колебания, возникающие в системе, которая в результате кратковременного внешнего воздействия выведена из положения равновесия и затем предоставлена самой себе. Если колебания такой системы происходят только под действием внутренних сил, которые, как правило, являются упругими или квазиупругими, то такие свободные колебания называются собственными. В реальных условиях свободные колебания носят затухающий характер

---

, так как они происходят при наличии различного вида сил сопротивления.

Системы, совершающие собственные колебания с одной степенью свободы, называются линейными гармоническими осцилляторами. Линейные осцилляторы совершают гармонические колебания лишь при малых отклонениях от положения равновесия. Таким образом, гармонический осциллятор - идеальная модель реальной колеблющейся системы с одной степенью свободы. Примерами гармонического осциллятора являются разные маятники, колебательный контур

.

3.2 Параметры гармонических колебаний

Пусть гармоническое колебание задано уравнением
, (4)
где А – амплитуда колебаний, представляет собой наибольшее отклонение системы от положения равновесия ( при );

- фаза колебаний, физическая величина, однозначно характеризующая состояния гармонического осциллятора в данный момент времени;

₀ – начальная фаза колебаний ( при t=0 );

 - циклическая частота собственных гармонических колебаний;

, т.е. циклическая частота является скоростью изменения фазы колебаний;

- линейная частота колебаний; она определяет число колебаний в единицу времени. Линейная частота связана с циклической частотой соотношением: .

Т- период колебаний, определяет время одного колебания
; (5)

 - разность фаз или сдвиг по фазе. Если

---

, то колебания происходят в одинаковой фазе, - в противофазе.

Значения А и ₀ определяются из начальных условий.

Найдем скорость гармонических колебаний, заданных уравнением (4), используя при этом обозначение: , тогда

. (6)

Определим ускорение гармонических колебаний:
, (7)
где .
3.3 Дифференциальное уравнение гармонических колебаний.
Формулу для ускорения гармонических колебаний (7) можно записать в виде:
,

тогда (8)
Уравнение (8) является дифференциальным уравнением гармонических колебаний. Легко убедиться подстановкой, что решением этого уравнения является выражение

Если какой-либо процесс, независимо от его природы, описывается дифференциальным уравнением (8), то этот процесс представляет собой гармоническое колебательное движение.

3.4 Математический маятник.

Математическим маятником называется тяжелая материальная точка, подвешенная на невесомой нерастяжимой нити. Из определения следует, что математическим маятником может служить любое тело, размеры которого пренебрежимо малы по сравнению с длиной нити, на которой оно подвешено.

Пусть шарик массы m подвешен на невесомой нерастяжимой нити длиной (рис.1). Если шарик вывести из положения равновесия, отклонив его на угол , то шарик будет совершать колебательное движение. Покажем, что при малых отклонениях колебания будут иметь гармонический характер.

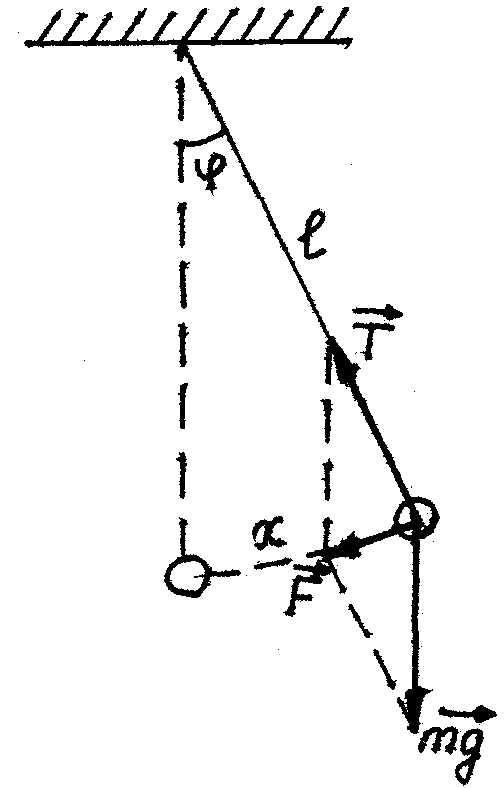Рисунок 1

На шарик действуют сила тяжести и сила натяжения нити . Результирующая сила возвращает шарик к положению равновесия. По второму закону Ньютона (9) Из рисунка 1 следует: (10) Знак (-) соответствует тому, что сила F направлена противоположено смещению шарика.

---

При малых углах , где x – смещение от положения равновесия. Учитывая, что ускорение , из уравнений (9) и (10) получим:
и . (11)
Уравнение (11) соответствует дифференциальному уравнению гармонических колебаний (8), следовательно, при малых отклонениях от положения равновесия математический маятник совершает гармонические колебания. Решение уравнения (11) имеет вид:
. (12)

Из сравнения уравнений (11) и (8) следует:
, . (13)
Выражение (13)– собственная частота колебаний математического маятника.

Период колебаний математического маятника
, . (14)
Таким образом, период колебаний математического маятника зависит от его длины и не зависит ни от амплитуды колебаний, ни от массы маятника.

4 Приборы и принадлежности
Установка FPM – 07, маятник с набором шаров различной массы, измерительная линейка.

5 Описание установки и метода измерений

Общий вид установки для выполнения данной работы изображен на рисунке 2.

Основание 1 снабжено регулируемыми ножками 2, которые позволяют произвести выравнивание прибора. В основании закреплена колонка 3, на которой зафиксирована стойка 4 с верхним 5 и нижним 6 кронштейнами. На нижнем кронштейне укреплены с одной стороны устройство 7 с градусной шкалой, позволяющее изменять угол наклона плоскости колебаний маятника, с другой стороны – фотоэлектрический датчик. В составе датчика имеется приемный фототранзистор 8 и осветительная лампочка 9. Над фототранзистором закреплена шкала 10, позволяющая измерять амплитуду колебаний маятника. Длину маятника можно регулировать, наматывая нить на винт 11. Фотоэлектрический датчик соединен с привинченным к основанию счетным устройством 12. Гнездо для подключения датчика расположено на задней панели счетного устройства. Схематический вид счетного устройства изображен на рисунке 2 (б). Элементы для текущего обслуживания прибора размещены на лицевой панели счетного устройства: 13 – окно счетчика периодов (числа колебаний); 14 – окно счетчика времени; 15, 16, 17 – клавиши управления.

---

Смотрите также файлы

• Наименование этапа античной философии и хронологические рамки.docx

• Синдромы поражения слизистой оболочки полости рта.docx

• Практическая работа к теме Эффективность работы классного руководителя (куратора) и ее оценка Успешные педагогические технологии, приемы, методы, которые позволили добиться намеченных результатов.docx

• Доклады Основные принципы государственной политики рф в области занятости населения Квотирование рабочих мест.docx

• Второй мировой войны оккупированная войсками.docx