Контрольные вопросы при изучении кинематики материальной точки при криволинейном движенииhttps://yandex.ru/video/preview/12547025900292727602[Ответы необходимо представлять в рукописном виде на каждый вопрос отдельно не более, чем на одном листе формата А4]

• 
  Дайте определение средней скорости и среднего ускорения, мгновенной скорости и мгновенного ускорения. Каковы их направления?
  

Средняя (путевая) скорость — это отношение длины пути, пройденного телом, ко времени, за которое этот путь был пройден: Средняя путевая скорость, в отличие от мгновенной скорости не является векторной величиной. Средняя скорость равна среднему арифметическому от скоростей тела во время движения только в том случае, когда тело двигалось с этими скоростями одинаковые промежутки времени.Вектором средней скорости назы­вается отношение приращения Dr радиуса-вектора точки к промежутку времени Dt:Направление вектора средней скоро­сти совпадает с направлением Dr. При неограниченном уменьшении Dt средняя скорость стремится к предельному значе­нию, которое называется мгновенной ско­ростью vСредним ускорением неравномерного движения в интервале от t до t+Dt на­зывается векторная величина, равная от­ношению изменения скорости Dv к интер­валу времени Dt:Мгновенным ускорением а материальной точки в момент време­ни t будет предел среднего ускорения:Мгновенная скорость v, таким образом, есть векторная величина, равная первой производной радиуса-вектора движущей­ся точки по времени. Так как секущая в пределе совпадает с касательной, то вектор скорости v направлен по касатель­ной к траектории в сторону движения (рис. 3). По мере уменьшения Dt путь Ds все больше будет приближаться к |Dr|, поэтому модуль мгновенной скорости

---

• 
  Что характеризуют тангенциальная и нормальная составляющие ускорения? Каковы их модули?
  

Тангенциальная составляющая ускорения характеризует быстроту изменения величины (модуля) скорости. Тангенциальное ускорение всегда коллинеарно скорости.Нормальная составляющая ускорения характеризует быстроту изменения скорости по направлению. Нормальное ускорение всегда перпендикулярно скорости и направлено к центру по радиусу траектории, по которой движется тело

• 
  Возможны ли движения, при которых отсутствуют нормальное и тангенциальное ускорения? Приведите примеры.
  
• 
  Что называют угловой скоростью и угловым ускорением движения тела?
  

• 
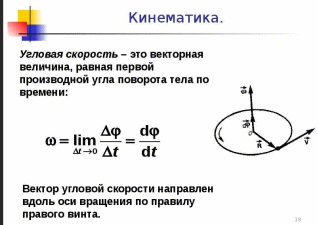
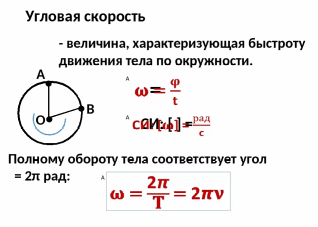
  Какова связь между линейными и угловыми величинами?
  

Понятно, что линейные и соответствующие им угловые величины должны быть определенным образом связаны между собой. Найдем эти связи.При повороте радиуса, проведенного в точку М (см. рис. 2), на угол φ точка пройдет по дуге окружности путьs=rφ . (1)За малое время Δt точка проходит расстояние Δs=rφ2−rφ1 , где φ2 и φ1 — углы поворота в конце и в начале интервала Δt. Разделив последнее равенство на Δt и учитывая, что ΔsΔt=υ и φ2−φ1Δt=ΔφΔt=ω, получимυ=rω . (2)Заметим, что соотношение (2) связывает между собой линейную и угловую скорости не только при равномерном движении точки по окружности, но- и при неравномерном движении тоже. Изменение модуля скорости точки за время Δt есть Δυ=rω2−rω1 , где ω2 и ω1 — угловые скорости в конце и в начале промежутка Δt. Разделим последнее равенство на Δt и учтем, что ΔυΔt=ak и ω2−ω1Δt=ΔωΔt=ε, тогда касательное ускорение

---

ak=rε . (3)Соотношения (1), (2) и (3) дают для движущейся по окружности точки простую связь между линейными и угловыми величинами: линейная величина равна произведению радиуса окружности на соответствующую угловую величину. Эти соотношения получены нами для конкретной точки М колеса троллейбуса, но они справедливы и для любой другой точки вращающегося (как равномерно, так и неравномерно) тела.

---

Смотрите также файлы

• Курсовая работа по дисциплине Технологии обработки информации Вариант 3 Фамилия Мельник.docx

• Методическая разработка внеклассного мероприятия по геометрии Математическое ассорти.docx

• Занятие 4 задание 1 Максимальное количество баллов 4.docx

• Общая характеристика правового положения гражданина (физических лиц) по гражданскому законодательству Российской Федерации.docx

• Протокол 5 от 15. 06. 2018г Календарный учебный график Муниципального бюджетного общеобразовательного учреждения.docx