Файл: Учебнометодическое пособие по дисциплине физика земли и атмосферы методические указания по выполнению.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 120
Скачиваний: 3
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
результаты угловых измерений содержат ошибку за влияние угловой рефракции. Величина угла рефракции зависит от градиента показателя преломления. На этом основании градиент показателя преломления можно считать «геодезическим» параметром атмосферы.
Линейные измерения. Для простоты будем считать, что показатель
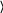 преломления вдоль визирного луча не меняется, т.е. n n const. Тогда в
преломления вдоль визирного луча не меняется, т.е. n n const. Тогда в
качестве рабочей формулы можно использовать зависимость (3). Представив зависимость (3) в дифференциальном виде, выразим истинную ошибку
расстояния D
через истинную ошибку показателя преломления
n. Для
простоты и наглядности прочие аргументы функции (3) будем считать безошибочными (т.е. при дифференцировании будем считать их константами):



 D dDn c n c 1 n D n.
D dDn c n c 1 n D n.
(7)
dn 2n2 2n n
Примечание.Формулу (7) можно использовать для определения истинной ошибки в расстоянии, если известна истинная ошибка определения показателя преломления, или
вернуться к исходному математическому пониманию n, как изменения (приращения)
показателя преломления. Тогда вопрос можно ставить по-другому: показатель преломления
изменился на n, а мы не учли это при вычислении расстояния, какова в этом случае будет
ошибка определения расстояния?
Воспользовавшись формулой средней квадратической ошибки функции общего вида, получим формулу, связывающую средние квадратические ошибки
определения показателя преломления mn
и расстояния
mD:
 mD D mn.
mD D mn.
(8)
Для измерения расстояния с точностью mD
показатель преломления
следует определять со средней квадратической ошибкой
 m mD.
m mD.
n D
(9)
Угловые измерения. Будем считать градиент показателя преломления в плоскости измерений в направлении, нормальном к визирному лучу, постоянным, т.е. gradn const, что позволит упростить формулу (6):
D
D
D2

r D gradnx x dx Dgradn x dx D
gradn .
2
0 0
В окончательном виде имеем:
r Dgradn.
2
(10)
В соответствии с формулой средней квадратической ошибки функции общего вида и зависимостью (10):
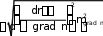 mr
mr
D

2
mgradn,
(11)
где
mr и
mgradn
– средние квадратические ошибки определения угла рефракции
и градиента показателя преломления. Тогда:
mgradn
2mr .
 D
D
(12)
Формула (12) позволяет оценить требования к точности определения градиента показателя преломления, если требования к точности угловых геодезических измерений заданы.
Пример 1. С какой средней квадратической ошибкой должен быть известен показатель преломления, если расстояние D≈1 км требуется получить с точностью 1 мм. Влиянием других источников погрешностей пренебречь.
Решение.Воспользуемся формулой (9):
m 103м 6
 mnD 10
mnD 10
1 N-ед.
D 103м
Вывод:для определения расстояния с относительной ошибкой 1/1 000 000 показатель преломления должен быть известен с точностью до миллионных долей (до 1 N-ед).
Пример 2. С какой точностью следует определять угол рефракции и градиент показателя преломления, если тригонометрическое нивелирование на линии длиной 1 км требуется выполнить с точностью геометрического нивелирования III класса, а влияние других источников погрешностей пренебрежимо мало? Дистанцию считать горизонтальной.
Решение.В соответствии с Инструкцией по нивелированию I, II, III и IV классов (Приложение 8.2) случайная средняя квадратическая ошибка определения превышения в нивелирной сети III класса равна 5 мм на 1 км хода. Превышение h вычисляют по формуле:
D
2
 h Dcos z i u , (13)
h Dcos z i u , (13)
2RЗ
где z– измеренное зенитное расстояние, iи u– высота инструмента и визирной цели, а RЗ – средний радиус кривизны Земли. Последний элемент в формуле
По условию, на точность определения превышения влияет только ошибка
угловых измерений. В этом случае ошибка
h определения превышения
связана с ошибкой Z
измерения зенитного расстояния формулой вида:
dh Dsin z ,


(14)
h dz Z
Z
а связь средних квадратических ошибок определения превышения mh и
зенитного расстояния mZ
характеризует следующая зависимость:
 Dsin z
Dsin z
m m.

h Z
Тогда
m
m.
(15)
ZDsin z h
Для нашего случая:
m 5мм 2,06 105
mZ h
1,0 .
Dsin z106 мм sin 90∘
Если считать, что ошибка измерения вертикального угла целиком обусловлена
влиянием ошибки определения угла рефракции:
mZ mr 1, то,
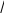 воспользовавшись формулой (12), получим требования к точности определения градиента показателя преломления:
воспользовавшись формулой (12), получим требования к точности определения градиента показателя преломления:
mgradn
2mr
 D
D
2 1
 2,06 105 103м
2,06 105 103м
108 м.
- Требования к точности определения показателя преломления и его градиента при геодезических измерениях
Линейные измерения. Для простоты будем считать, что показатель
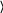 преломления вдоль визирного луча не меняется, т.е. n n const. Тогда в
преломления вдоль визирного луча не меняется, т.е. n n const. Тогда вкачестве рабочей формулы можно использовать зависимость (3). Представив зависимость (3) в дифференциальном виде, выразим истинную ошибку
расстояния D
через истинную ошибку показателя преломления
n. Для
простоты и наглядности прочие аргументы функции (3) будем считать безошибочными (т.е. при дифференцировании будем считать их константами):



 D dDn c n c 1 n D n.
D dDn c n c 1 n D n.(7)
dn 2n2 2n n
Примечание.Формулу (7) можно использовать для определения истинной ошибки в расстоянии, если известна истинная ошибка определения показателя преломления, или
вернуться к исходному математическому пониманию n, как изменения (приращения)
показателя преломления. Тогда вопрос можно ставить по-другому: показатель преломления
изменился на n, а мы не учли это при вычислении расстояния, какова в этом случае будет
ошибка определения расстояния?
Воспользовавшись формулой средней квадратической ошибки функции общего вида, получим формулу, связывающую средние квадратические ошибки
определения показателя преломления mn
и расстояния
mD:
 mD D mn.
mD D mn.(8)
Для измерения расстояния с точностью mD
показатель преломления
следует определять со средней квадратической ошибкой
 m mD.
m mD.n D
(9)
Угловые измерения. Будем считать градиент показателя преломления в плоскости измерений в направлении, нормальном к визирному лучу, постоянным, т.е. gradn const, что позволит упростить формулу (6):
D
D
D2

r D gradnx x dx Dgradn x dx D
gradn .
2
0 0
В окончательном виде имеем:
r Dgradn.
2
(10)
В соответствии с формулой средней квадратической ошибки функции общего вида и зависимостью (10):
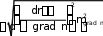 mr
mr D

2
mgradn,
(11)
где
mr и
mgradn
– средние квадратические ошибки определения угла рефракции
и градиента показателя преломления. Тогда:
mgradn
2mr .
 D
D(12)
Формула (12) позволяет оценить требования к точности определения градиента показателя преломления, если требования к точности угловых геодезических измерений заданы.
Примеры решения задач
Пример 1. С какой средней квадратической ошибкой должен быть известен показатель преломления, если расстояние D≈1 км требуется получить с точностью 1 мм. Влиянием других источников погрешностей пренебречь.
Решение.Воспользуемся формулой (9):
m 103м 6
 mnD 10
mnD 10 1 N-ед.
D 103м
Вывод:для определения расстояния с относительной ошибкой 1/1 000 000 показатель преломления должен быть известен с точностью до миллионных долей (до 1 N-ед).
Пример 2. С какой точностью следует определять угол рефракции и градиент показателя преломления, если тригонометрическое нивелирование на линии длиной 1 км требуется выполнить с точностью геометрического нивелирования III класса, а влияние других источников погрешностей пренебрежимо мало? Дистанцию считать горизонтальной.
Решение.В соответствии с Инструкцией по нивелированию I, II, III и IV классов (Приложение 8.2) случайная средняя квадратическая ошибка определения превышения в нивелирной сети III класса равна 5 мм на 1 км хода. Превышение h вычисляют по формуле:
D
2
 h Dcos z i u , (13)
h Dcos z i u , (13)2RЗ
где z– измеренное зенитное расстояние, iи u– высота инструмента и визирной цели, а RЗ – средний радиус кривизны Земли. Последний элемент в формуле
-
представляет собой поправку за кривизну Земли.
По условию, на точность определения превышения влияет только ошибка
угловых измерений. В этом случае ошибка
h определения превышения
связана с ошибкой Z
измерения зенитного расстояния формулой вида:
dh Dsin z ,


(14)
h dz Z
Z
а связь средних квадратических ошибок определения превышения mh и
зенитного расстояния mZ
характеризует следующая зависимость:
 Dsin z
Dsin zm m.

h Z
Тогда
m
m.
(15)
ZDsin z h
Для нашего случая:
m 5мм 2,06 105
mZ h
1,0 .
Dsin z106 мм sin 90∘
Если считать, что ошибка измерения вертикального угла целиком обусловлена
влиянием ошибки определения угла рефракции:
mZ mr 1, то,
 воспользовавшись формулой (12), получим требования к точности определения градиента показателя преломления:
воспользовавшись формулой (12), получим требования к точности определения градиента показателя преломления:mgradn
2mr
 D
D 2 1
 2,06 105 103м
2,06 105 103м 108 м.