Файл: Учебнометодическое пособие по дисциплине физика земли и атмосферы методические указания по выполнению.docx

Вывод:для определения превышения методом тригонометрического нивелирования на линии длиной 1 км с точностью геометрического нивелирования III класса угол рефракции должен быть известен с точностью 1^, а

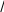градиент показателя преломления – со средней квадратической ошибкой 10^⁸ м .

Показатель преломления и его градиент как функции метеопараметров. Требования к точности определения метеопараметров и их градиентов при геодезических измерениях

Линейные измерения. Линейные геодезические измерения выполняют в оптическом диапазоне (электронная тахеометрия) и радиодиапазоне (спутниковые измерения). В оптическом диапазоне показатель преломления и индекс преломления, связанный с ним функционально, являются функциями температуры, давления, влажности воздуха и длины волны излучения. При измерениях в световом диапазоне (видимая часть спектра) для определения индекса преломления используют формулу Сирса-Баррела в виде:

N _n1_10⁶  83,11 ^p11, 4 ^e,

T T
(16)

где

T, p и e

–

температура, давление и влажность (парциальное давление

водяного пара) воздуха в К и гПа.

Зависимость индекса преломления от метеопараметров в радиодиапазоне описывает формула Фрума-Эссена:

N _n1_10⁶  77,63 ^p12,92 ^e

 371914 ^e.
(17)

T T T²

Изменение метеопараметров приведет к изменению показателя преломления:

N ^^NT ^^Np ^^Ne.

(18)

T p e

Точность определения показателя преломления в точке зависит от точности измерения температуры, давления и влажности воздуха. Воспользуемся формулой средней квадратической ошибки функции общего вида для того чтобы выразить ошибку определения индекса преломления через ошибки определения аргументов T, p и e:

m_N

. (19)

Примечание. В формулах (16) и (17) используется абсолютная температура T, выраженная в Кельвинах, для перехода от температуры t в градусах Цельсия к абсолютной температуре используют соотношение:

T=t+273,15.
Однако цена деления на шкалах Цельсия и Кельвина одинаковая. Поэтому в тех случаях, когда речь идет не о температуре, а об ее изменении (истинной ошибке) или ее средней квадратической ошибке, используемая размерность не имеет значения и переход от одной шкалы к другой не требуется:

T t;
m m;

 ^^N _ ^^N_.

T t  __T  __t

   

В Таблице приведены значения частных производных функций (16) и (17), вычисленные для нормальных условий (T – 293,15 К, p – 1013,25 гПа, e –13,33 гПа ).

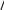
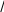
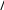
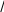
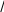Таблица – Значения частных производных показателя преломления в оптическом и радио- диапазонах

Производная	Оптический диапазон	Радиодиапазон
nT	110^⁶ K	1,3 10^⁶ K
np	0,3 10^⁶ гПа	0,3 10^⁶ гПа
ne	0,04 10^⁶ гПа	4,3 10^⁶ гПа

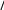
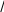Примечание.Согласно данным Таблицы, изменение температуры на 1 К приведет к изменению показателя преломления на 1 N-ед., если пренебречь таким изменением состояния атмосферы ошибка определения расстояния составит 1 мм/км (см. Пример1на стр. 12). Изменение давления на 1 гПа приведет к ошибкам определения показателя преломления и расстояния, равным 0,3 N-ед. и 1 мм/км, соответственно. Неучтенная ошибка во влажности, равная 1 гПа, в оптическом диапазоне приведет к ошибке определения расстояния, равной 0,04 мм/км, в радиодиапазоне соответствующая ошибка в расстоянии будет равна 4,3 мм/км.

На основании данных Таблицы и приведенных рассуждений можно сделать вывод о пренебрежимо малом влиянии влажности в оптическом диапазоне.

Угловые измерения. Разделив все члены формулы (18) на Δy, получим приближенную формулу, выражающую градиент показателя преломления световых волн через градиенты метеопараметров при нормальных условиях (воспользуемся второй колонкой Таблицы):

gradn 110^⁶ gradT 0,3 10^⁶ gradp 0,04 10^⁶ grade.

(20)

Примечания:

Формулу (20) можно использовать только для приближенных точностных расчетов. Использовать ее для вычисления градиента показателя преломления и последующей коррекции угловых измерений за влияние рефракции нельзя! Она не отвечает геодезическим требованиям к точности определения градиента показателя преломления (см. Пример 2 на стр. 12-13).
В физике атмосферы горизонтальные градиенты считают положительными, если они направлены в сторону уменьшения метеопараметра. Вертикальный градиент всегда направлен вверх. Если метеопараметр с высотой уменьшается (нормальный ход) – вертикальный градиент положительный, если метеопараметр растет с высотой (инверсия) – градиент отрицательный.