Виды используемых циклов.

1.Цикл while (“пока”). Позволяет выполнить одну и ту же последовательность действий, пока проверяемое условие истинно. Условие записывается до тела цикла и проверяется до выполнения тела цикла. Как правило, цикл while используется, когда невозможно определить точное значение количества проходов исполнения цикла.

2.Цикл for, также называемый циклом с параметром, в языке Питон богат возможностями. В цикле for указывается переменная и множество значений, по которому будет пробегать переменная. Множество значений может быть задано списком, кортежем, строкой или диапазоном (будет рассматриваться в следующей лабораторной работе).

Пример. Вывод таблицы значений функции

Постановка. Вывести таблицу значений заданной функции на отрезке и с шагом, которые вводит пользователь.

Пусть функция будет такой: y = -3x² - 4x + 20.

Метод решения.

1. 
   Запросить у пользователя точки начала и конца отрезка, а также шаг.
   
2. 
   Если значение точки начала отрезка больше значения точки конца, то поменять значения.
   
3. 
   Пока значение первой точки не достигнет второй
   
4. 
   вычислить значение функции,
   
5. 
   вывести на экран текущие значения x и y,
   
6. 
   увеличить значение первой точки на шаг.
   

Реализация на Python


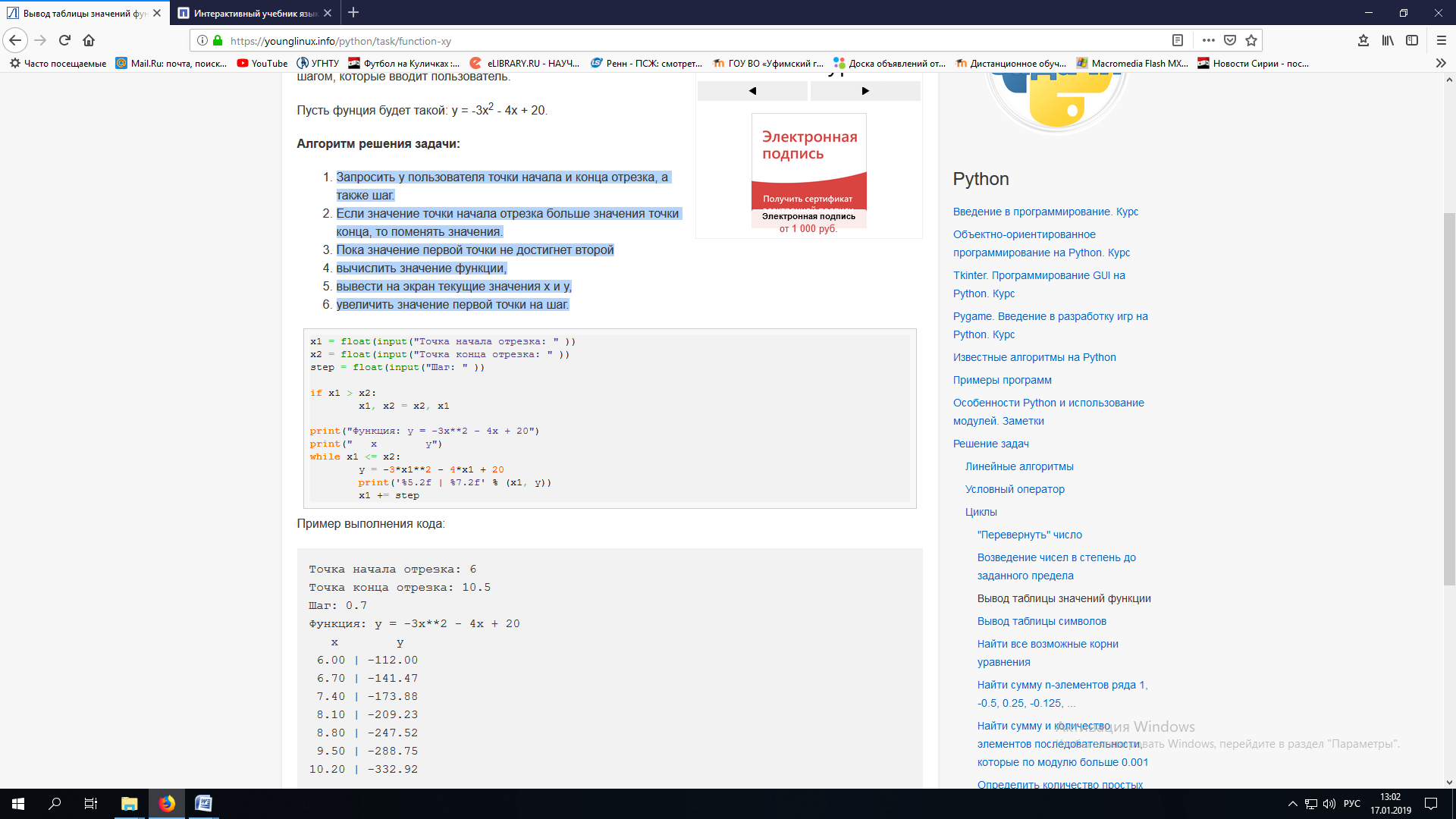
Проверка результата:
Точка начала отрезка: 6

Точка конца отрезка: 10.5

Шаг: 0.7

Функция: y = -3x**2 - 4x + 20

x y

6.00 | -112.00

6.70 | -141.47

7.40 | -173.88

8.10 | -209.23

8.80 | -247.52

9.50 | -288.75

10.20 | -332.92
Здесь использовались форматы вывода:



1.3 Пример выполнения лабораторной работы
Задание 1. Составить программу линейного алгоритма для вычисления значения:


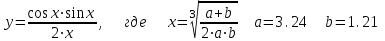
Составляем программу:



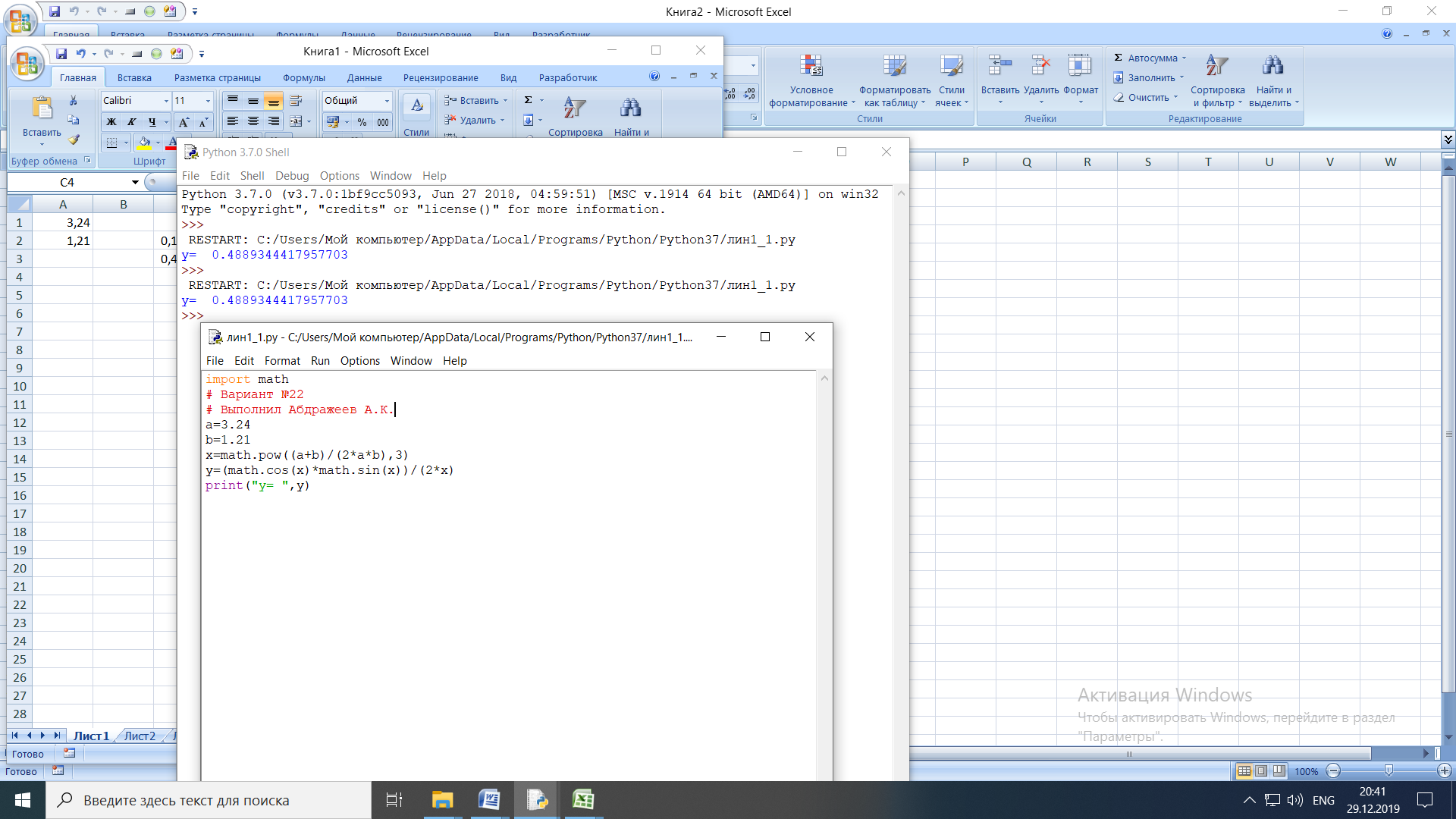
Результат:



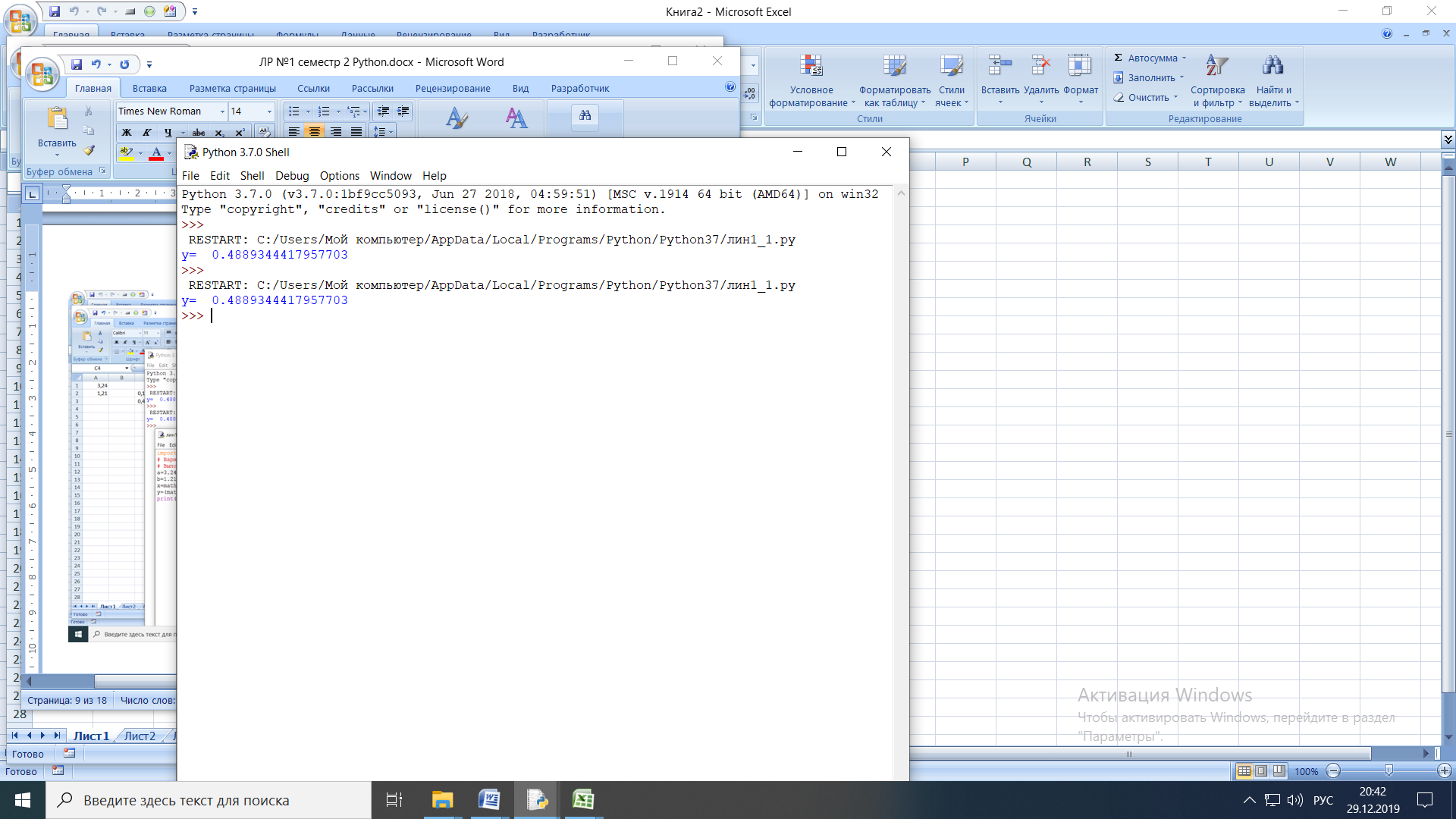
Примечание. В комментариях следует указать автора, т.е. кто выполнил (свою фамилию и номер группы), а также все переменные. В случае если по каким-либо причинам не укажете, то оценка за работу будет снижена.

---

Задание 2. Составить программу разветвляющего алгоритма вычисления значения:


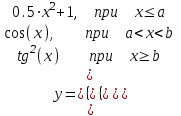
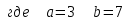
Составляем программу:



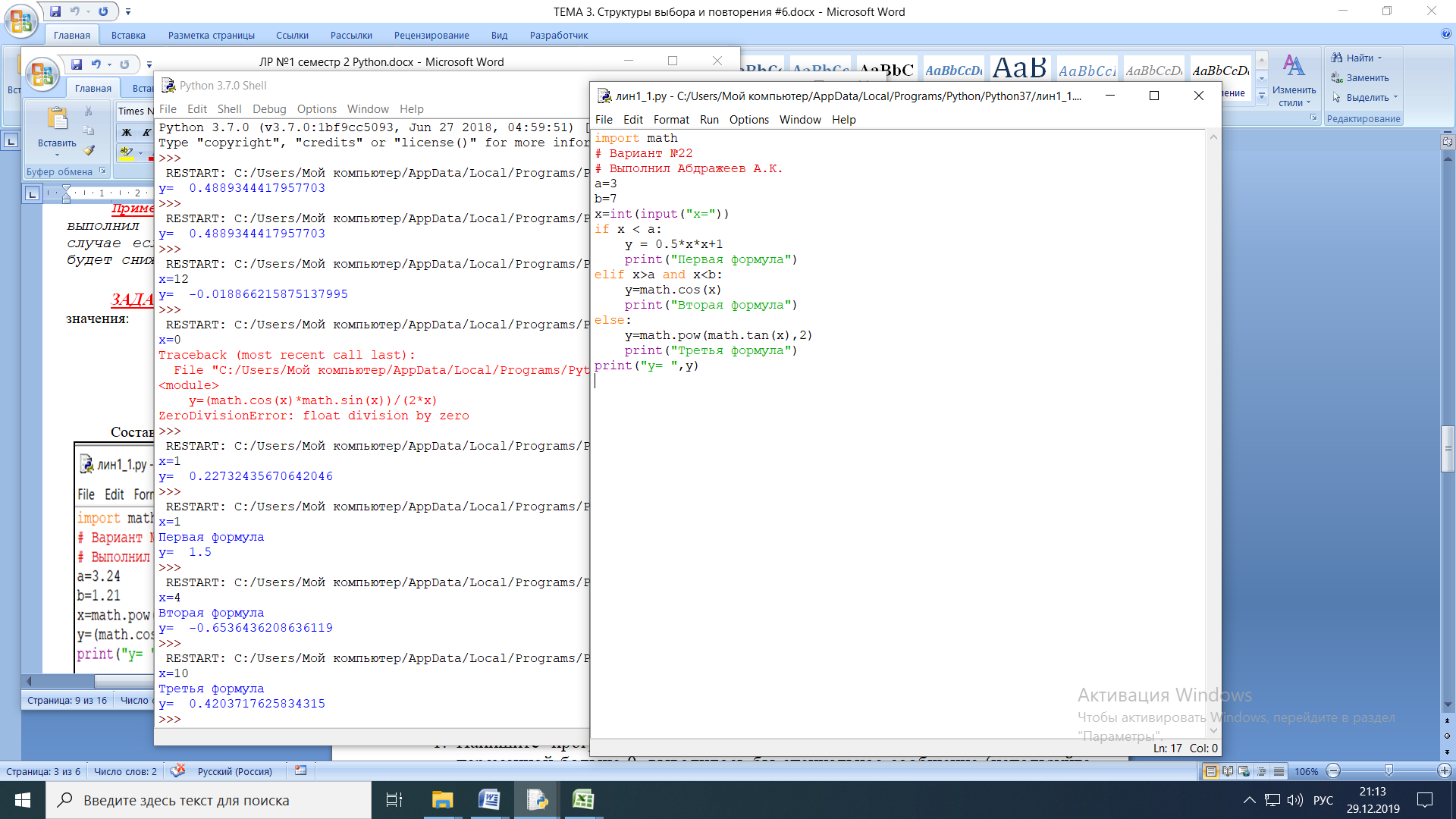
Результат:


Задание 3. Пример 3. Составить программу нахождения суммы следующего выражения:

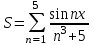где x - любое не равное нулю и единице число

Составляем программу:



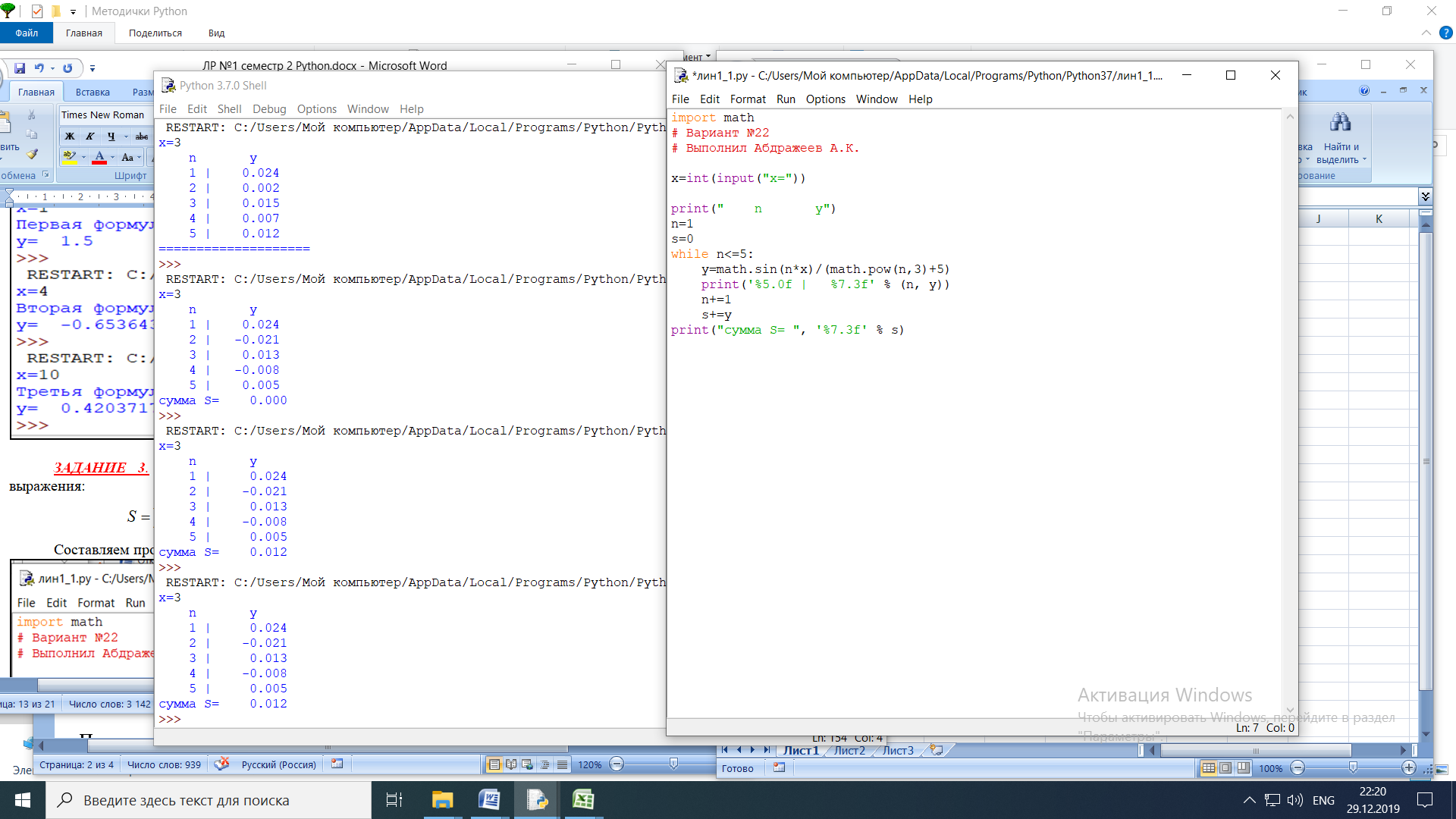
Результат:



1.4 варианты для выполнения лабораторной работы

Задание №1: Разработайте линейный алгоритм и представьте его в графическом виде (блок-схемы). Вычислить значение выражения s при заданных исходных данных.

Указание. Для упрощения выражений можно ввести промежуточные переменные.

Вариант	Исходные данные	Функция
1	x = 14.26 y = – 1.22 z = 3.5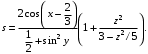
2	x = –4.5 y = 0.75 z = –0.845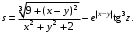
3	x = 3.74 y= –0.825 z = 0.16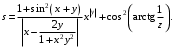
4	x = 0.4 y = –0.875 z = –0.475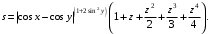
5	x = –15.246 y = 4.642 z = 21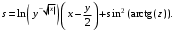
6	x = 16.55 y = –2.75 z = 0.15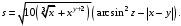
7	x = 0.1722 y = 6.33 z = 3.25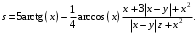
8	x = –2.235 y = 2.23 z = 15.221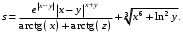
9	x = 1.825 y = 18.225 z = –3.298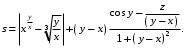
10	x = 3.981 y = –1.625 z = 0.512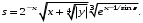
11	x = 6.251 y = 0.827 z = 25.001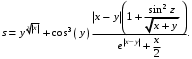
12	x = 3.251 y = 0.325 z = 0.466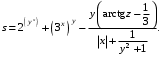
13	x = 17.421 y = 10.365 z = 0.828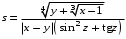
14	x = 12.3 y = 15.4 z = 0.252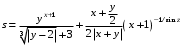
15	x = 2.444 y = 0.869 z = –0.13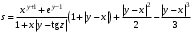
16	x = –1,42 y = 1,22 z = –1,82 a = –18,25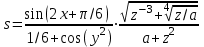
17	a = 1,378 b = –2,2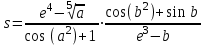
18	x = –0,765 a = 3,2 b = 17,5 p = 0,137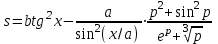
19	x = –1,42 y = 1,22 x = 1,71 m = –2,2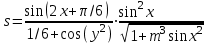
20	x = 0,515 c = 3,75 b = 0,0002 a = 0,17 x = 7,75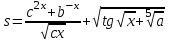

---

Задание №2: Разработайте алгоритм разветвляющего процесса и представьте его в графическом виде (блок-схемы). Вычислить значение выражения y при заданных исходных данных.

Указание. Для упрощения выражений можно ввести промежуточные переменные.

Вариант	Исходные данные	Функция
1	z =  2,3 x= -4,5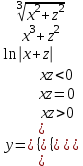
2	a = -3,14 x= -5,7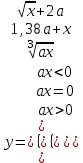
3	a = 0,12 b = –4,4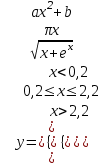
4	с = 0,04 x = 31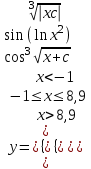
5	L = 6,2 x= 0,2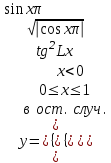
6	a = 2,8 x = 5,3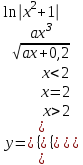
7	a = 0,01 b = –2 x = –3,6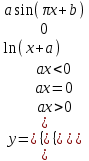
8	a = 98,3 b = 4,5 x = 1,8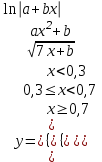
9	a = 2,81 b = 5,96 x = 3,2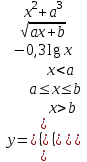
10	a = 4,4 x= –7,5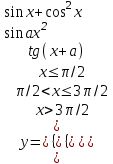
11	a = 2 x = 9,9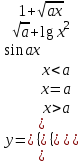
12	a  = 11,3 x = 2,2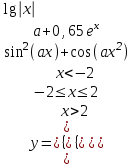
13	a = 0,1 x = 2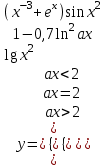
14	a = 7,13 b = 0,91 x = –4,4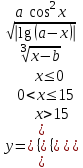
15	w = 1,2 x = 3,1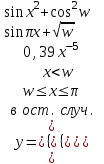
16	d = 2,5 x = –25,1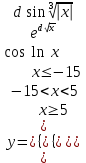
17	b = 0,91 x = 19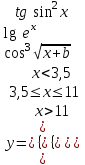
18	k = 9,1 x = 1,9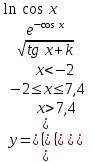
19	a = 3,8 x = –5,1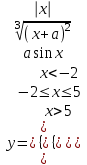
20	a = 98,3 b = 4,5 x = 1,8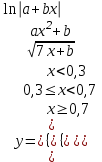

---

Задание №3: Разработайте циклический алгоритм вычисления суммы 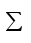(произведения 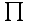) конечного числа элементов ряда и представьте его в графическом виде (блок-схемы).

Вычислить значение выражения при заданных исходных данных.

Вариант	Исходные данные	Функция
1	x=3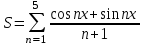
2	x=4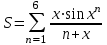
3	ничего не вводится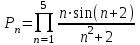
4	x=3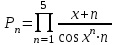
5	x=5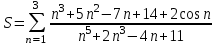
6	x=3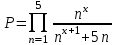
7	ничего не вводится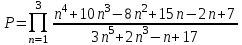
8	ничего не вводится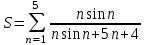
9	x=5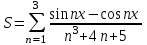
10	ничего не вводится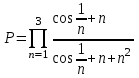
11	a = 3 b = 2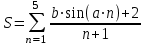
12	x =4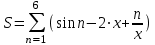
13	ничего не вводится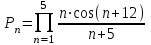
14	x =4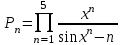
15	b = 2 х = 3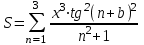
16	x = 3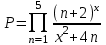
17	b = 5 х = 3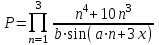
18	a = 3 х = 3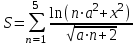
19	x = 3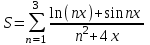
20	x = 4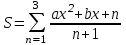

---

ПРИЛОЖЕНИЕ 1.

Функционал модуля Math
math.ceil(X) – округление до ближайшего большего числа.

math.copysign(X, Y) - возвращает число, имеющее модуль такой же, как и у числа X, а знак - как у числа Y.

math.fabs(X) - модуль X.

math.factorial(X) - факториал числа X.

math.floor(X) - округление вниз.

math.fmod(X, Y) - остаток от деления X на Y.

math.frexp(X) - возвращает мантиссу и экспоненту числа.

math.ldexp(X, I) - X * 2ⁱ. Функция, обратная функции math.frexp().

math.fsum(последовательность) - сумма всех членов последовательности. Эквивалент встроенной функции sum(), но math.fsum() более точна для чисел с плавающей точкой.

math.isfinite(X) - является ли X числом.

math.isinf(X) - является ли X бесконечностью.

math.isnan(X) - является ли X NaN (Not a Number - не число).

math.modf(X) - возвращает дробную и целую часть числа X. Оба числа имеют тот же знак, что и X.

math.trunc(X) - усекает значение X до целого.

math.exp(X) - e^X.

math.expm1(X) - e^X - 1. При X → 0 точнее, чем math.exp(X)-1.

math.log(X, [base]) - логарифм X по основанию base. Если base не указан, вычисляется натуральный логарифм.

math.log1p(X) - натуральный логарифм (1 + X). При X → 0 точнее, чем math.log(1+X).

math.log10(X) - логарифм X по основанию 10.

math.log2(X) - логарифм X по основанию 2.

math.pow(X, Y) - X^Y.

math.sqrt(X) - квадратный корень из X.

math.acos(X) - арккосинус X. В радианах.

math.asin(X) - арксинус X. В радианах.

math.atan(X) - арктангенс X. В радианах.

math.atan2(Y, X) - арктангенс Y/X. В радианах. С учетом четверти, в которой находится точка (X, Y).

math.cos(X) - косинус X (X указывается в радианах).

math.sin(X) - синус X (X указывается в радианах).

math.tan(X) - тангенс X (X указывается в радианах).

math.hypot(X, Y) - вычисляет гипотенузу треугольника с катетами X и Y (math.sqrt(x * x + y * y)).

math.degrees(X) - конвертирует радианы в градусы.

math.radians(X) - конвертирует градусы в радианы.

math.cosh(X) - вычисляет гиперболический косинус.

math.sinh(X) - вычисляет гиперболический синус.

math.tanh(X) - вычисляет гиперболический тангенс.

math.acosh(X) - вычисляет обратный гиперболический косинус.

math.asinh(X) - вычисляет обратный гиперболический синус.

math.atanh(X) - вычисляет обратный гиперболический тангенс.

math.erf(X) - функция ошибок.

math.erfc(X) - дополнительная функция ошибок (1 - math.erf(X)).

math.gamma(X) - гамма-функция X.

math.lgamma(X) - натуральный логарифм гамма-функции X.

math.pi - pi = 3,1415926...

math.e - e = 2,718281...

---

Смотрите также файлы

• Учебного предмета на соответствие требованиям фгос ноо (фрагмент) Позиция для оценки.docx

• Рефераты Восприятие несовершеннолетними осужденными тюремной субкультуры в зависимости от отбытого срока лишения свободы.docx

• Биофизика курсымен алыпты физиология.doc

• Высшего Образования новосибирский государственный педагогический университет.docx

• Занятие для обучающихся спо по теме день труда. Мир профессий.pdf