Файл: Трехфазные и многофазные цепи и системы, основные понятия и определения.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 18
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
20 вопрос:
Трехфазные и многофазные цепи и системы, основные понятия и определения.
Трехфазная цепь является частным случаем многофазных систем электрических цепей, представляющих собой совокупность электрических цепей, в которых действуют синусоидальные ЭДС одинаковой частоты, отличающиеся по фазе одна от другой и создаваемые общим источником энергии.
Каждую из частей многофазной системы, характеризующуюся одинаковым током, принято называть фазой. Таким образом, понятие "фаза" имеет в электротехнике два значения: первое – аргумент синусоидально изменяющейся величины, второе – часть многофазной системы электрических цепей. Цепи в зависимости от количества фаз называют двухфазными, трехфазными, шестифазными и т.п.
Трехфазные цепи – наиболее распространенные в современной электроэнергетике. Это объясняется рядом их преимуществ по сравнению как с однофазными, так и с другими многофазными цепями:
-
экономичность производства и передачи энергии по сравнению с однофазными цепями; -
возможность сравнительно простого получения кругового вращающегося магнитного поля, необходимого для трехфазного асинхронного двигателя; -
возможность получения в одной установке двух эксплуатационных напряжений – фазного и линейного.
Трехфазная цепь состоит из трех основных элементов: трехфазного генератора, в котором механическая энергия преобразуется в электрическую с трехфазной системой ЭДС; линии передачи со всем необходимым оборудованием; приемников (потребителей), которые могут быть как трехфазными (например, трехфазные асинхронные двигатели), так и однофазными (например, лампы накаливания).
21 вопрос:
Цепи периодического несинусоидального тока. Несинусоидальные ЭДС и токи.
Разложение несинусоидальных периодических функций в ряд Фурье.
Определение периодических несинусоидальных токов и напряжений.
Периодическими несинусоидальными токами и напряжениями называют токи и напряжения, изменяющиеся во времени по периодическому несинусоидальному закону.
Они возникают при четырех различных режимах работы электрических цепей (и при сочетаниях этих режимов):
1) когда источник ЭДС (источник тока) дает несинусоидальную ЭДС (несинусоидальный ток), а все элементы цепи — резистивные, индуктивные и емкостные — линейны, т. е. от тока не зависят;
2) если источник ЭДС (источник тока) дает синусоидальную ЭДС (синусоидальный ток), но один или несколько элементов цепи нелинейны;
3) когда источник ЭДС (источник тока) дает несинусоидальную ЭДС (несинусоидальный ток), а в состав электрической цепи входят один или несколько нелинейных элементов;
4) если источник ЭДС (тока) дает постоянную или синусоидальную ЭДС (ток), а один или несколько элементов цепи периодически изменяются во времени.
Изображение несинусоидальных токов и напряжений с помощью рядов Фурье
Определение: Любая периодическая функция, может быть разложена в ряд Фурье, т.е. представлена в виде бесконечного ряда гармонических составляющих:
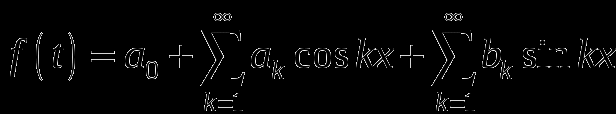
где – постоянная составляющая (нулевая гармоника);
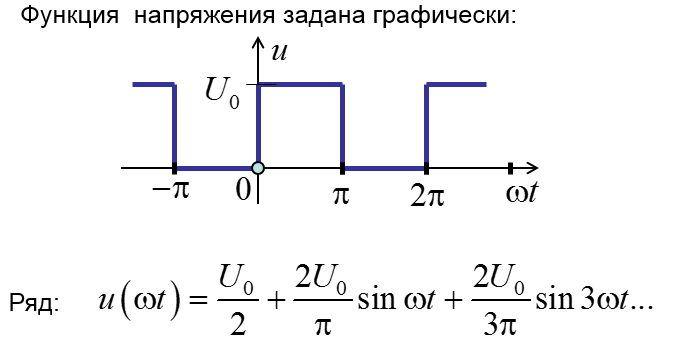
Пример разложения несинусоидальной кривой напряжения в ряд Фурье
Функция напряжения задана графически:
Действующее значение несинусоидального тока
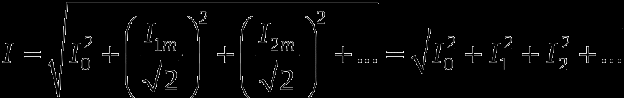
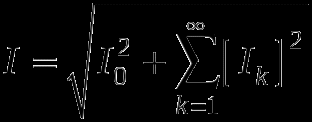
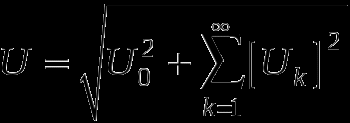
22 вопрос:
Действующие значение периодических несинусоидальных ЭДС , напряжений, токов.
23 вопрос:
Расчет цепей с несинусоидальными периодическими ЭДС и токами.
Расчет линейной электрической цепи с несинусоидальными ЭДС выполняется на основе принципа наложения.
Согласно этому принципу ток (напряжение) на любом участке цепи определяется как алгебраическая сумма токов (напряжений) отдельных гармоник на этом участке.
Индуктивные и емкостные сопротивления цепи определяются циклической частотой.
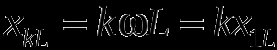
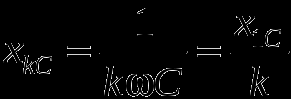
где
Последовательность расчета
1) Представляем несинусоидальный источник энергии в виде ряда Фурье;
2) Выполняем расчет от действия нулевой гармоники (постоянной составляющей), полагая, что емкость для цепи является разрывом , индуктивность закороткой
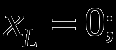
3) Выполняем расчет от действия первой гармоники;
4) Выполняем расчет от действия гармоники более высокого порядка, предварительно производя пересчет:
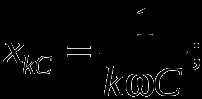
5) Применяя метод наложения, определяем мгновенные или действующие значения величин.
24 вопрос :
Переходные процессы в линейных цепях. Общие понятия и определения. Правила коммутации.
Природа переходных процессов
Переходные процессы возникают при включении или отключении источников питания, элементов цепи, при коротких замыканиях и обрывах проводов, а также при различных импульсных воздействиях на цепь
ОПРЕДЕЛЕНИЕ ПЕРЕХОДНОГО ПРОЦЕССА
Переходным процессом в электрической цепи называется процесс перехода цепи из одного установившегося состояния или режима в другое установившееся состояние (режим) отличающееся от предыдущего, например амплитудой или начальной фазой.
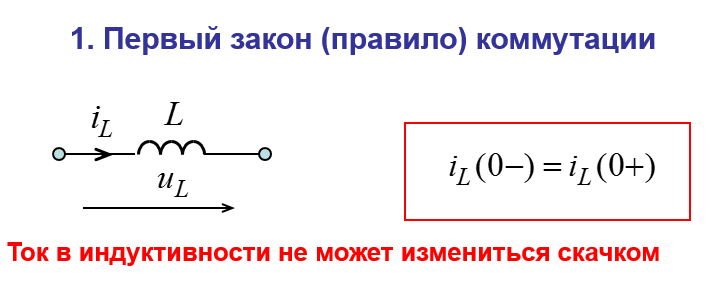
При анализе и расчете переходных процессов будем считать что переходные процессы возникают при включении или отключении элементов цепи посредством ключей.
Процесс замыкания или размыкания ключа будем называть коммутацией соответствующей моменту времени t= 0
 Ключ замыкается:
Ключ замыкается: Ключ размыкается:

Цепь характеризуется моментами времени которые определяют состояние цепи:

25 вопрос :
Начальные условия. Зависимые и независимые начальные условия. Нулевые и ненулевые начальные условия. Примеры.
Начальные условия (Н.У.)
Под начальными условиями понимаются значения токов и напряжений в момент коммутации, т.е. при t= 0.
1. К независимым начальным условиям относятся величины, которые не изменяют своих значений в момент коммутации, при t= (0+).
2. К зависимым начальным условиям относятся все остальные условия: токи напряжения их производные, которые изменяют свои значения в момент коммутации, при t= (0+).


26 вопрос :
Классический метод расчета переходных процессов. Характеристическое уравнение цепи.
27 вопрос :
Переходные процессы в цепях первого порядка. Включение цепи r, L на постоянное напряжение. Короткое замыкание r, L цепи.
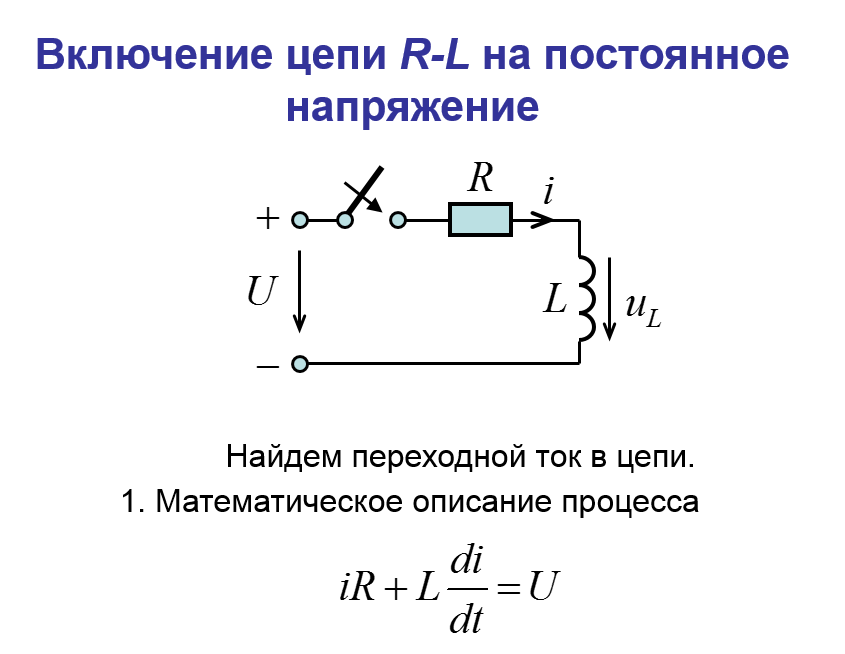
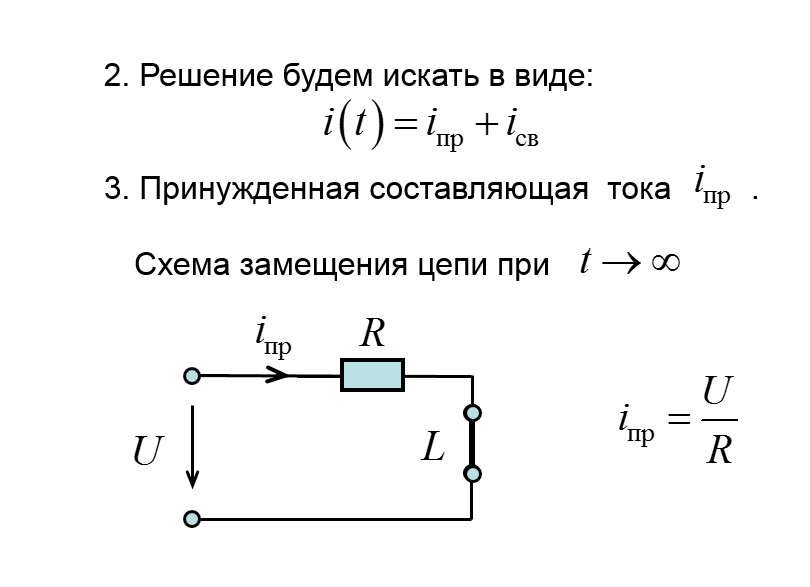

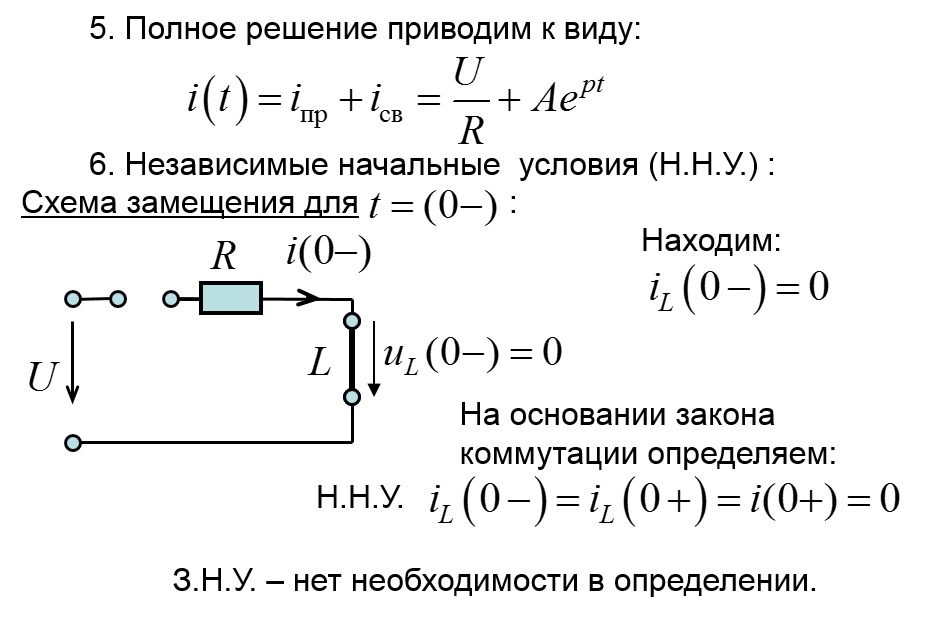

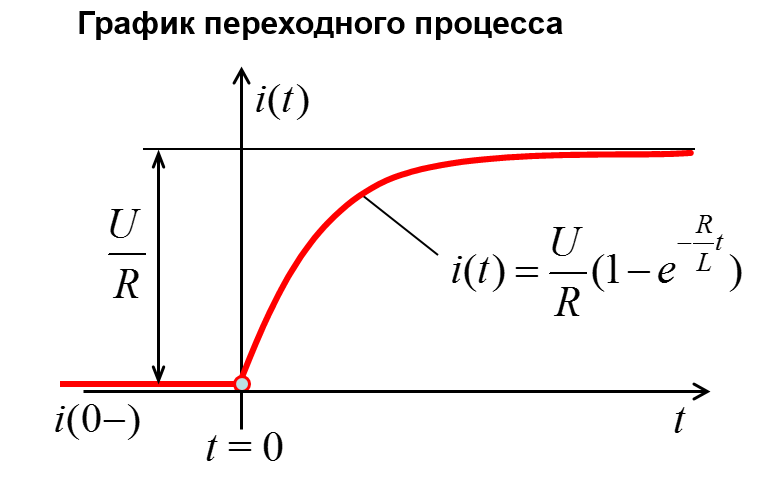
28 вопрос :
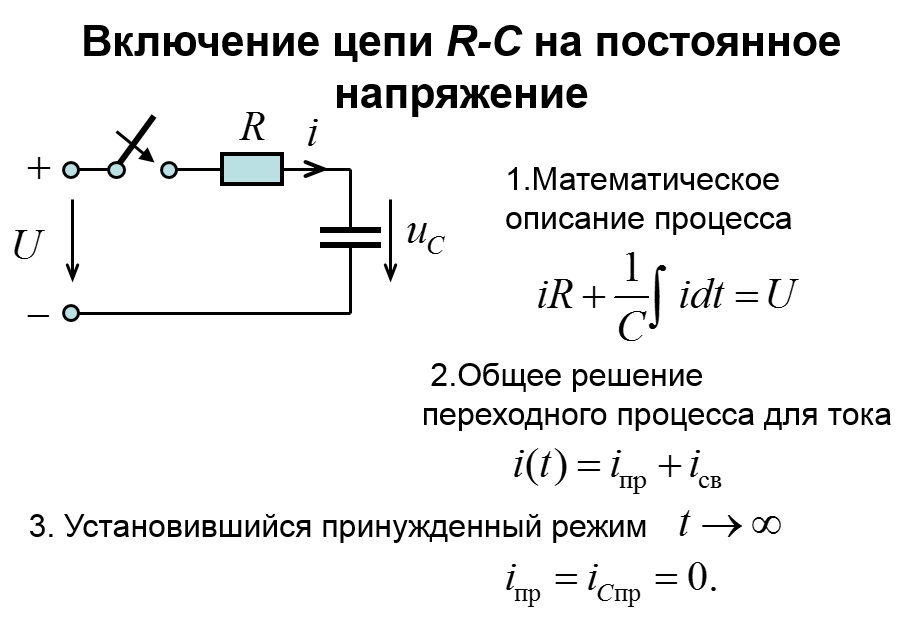
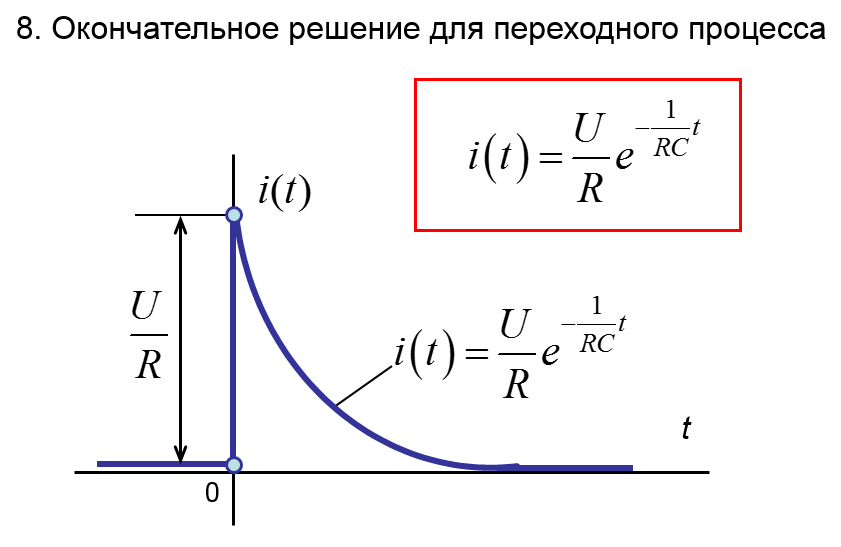
Включение r, C цепи на постоянное напряжение. Короткое замыкание r, C цепи.