Файл: Краткосрочный план кгу Средняя школа 23 им. М шаяхметова.doc
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 33
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Краткосрочный план №
КГУ «Средняя школа №23 им.М Шаяхметова» отдела образования по городу Усть-Каменогорску управления образования ВКО
Соотношения между сторонами и углами прямоугольного треугольника
тема урока
| Раздел: | 8.2AСоотношения между сторонами и углами прямоугольного треугольника | |
| ФИО педагога | Кирдьянова Т.Н | |
| Дата: | 10.05.2023(16.05.2023) | |
| Класс: 8 | Количество присутствующих: | Количество отсутствующих: |
| Тема урока | Решение прямоугольных треугольников | |
| Цели обучения в соответствии с учебной программой | 8.1.3.8 находить стороны и углы прямоугольного треугольника по двум заданным элементам; | |
| Цели урока | находит стороны и углы прямоугольного треугольника по двум заданным элементам; | |
Ходурока
| Этап урока/ Время | Действия педагога | Действия ученика | Оценивание | Ресурсы | ||||||||||||
| Начало урока Середина урока Конец урока |
Среди многоугольников прямоугольный треугольник играет особую роль. Действительно, любой многоугольник можно разбить на треугольники, умея находить угловые и линейные элементы этих треугольников, можно найти все элементы многоугольника. В свою очередь, любой треугольник можно разбить одной из его высот на два прямоугольных треугольника, элементы которых связаны более простой зависимостью. Найти элементы треугольника можно. Если свести задачу к решению этих двух прямоугольных треугольников. Что значит решить треугольник?
Вставить пропущенные слова:
- Достаточно ли знать значения тригонометрических функций некоторых углов, чтобы решать практические задачи? Знакомство с четырехзначной математической таблицей В. Брадиса. Её использовали когда нет инженерного калькулятора Работа в парах Оценка умения использовать таблицу Брадиса. Работа в группах. Разбить класс на свое усмотрение по группам и раздать задания. Выполнив задание, группа презентует решение остальным группам. Учитель может задать уточняющие вопросы, чтобы убедиться, что все члены группы хорошо понимают представленное решение. Группы используют таблицу для оценивания:
После выступлений групп учитель дополняет и обобщает сказанное и выводит алгоритмы Рефлексия. Беседа. - Что узнали, чему научились? - Что осталось не понятным? - Над чем необходимо поработать? Домашнее задание. | Ответ учащихся. Найти остальные стороны и/или углы треугольника по уже известным. При поддержки учителя определить тему и цели урока Вставляют пропущенные слова
Выполняют задания Вычислите:
Найдите величину острого угла, если Алгоритм№ 1. Дано: два катета п 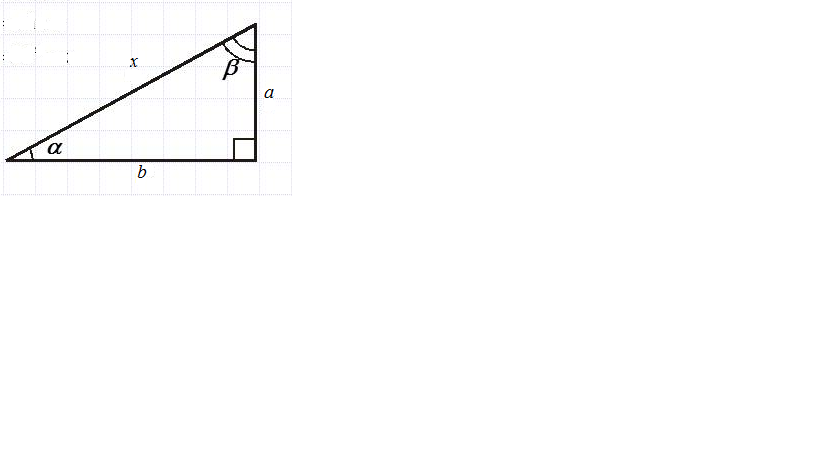 рямоугольного треугольника. рямоугольного треугольника.Алгоритм № 2. Дано: Гипотенуза и острый угол. 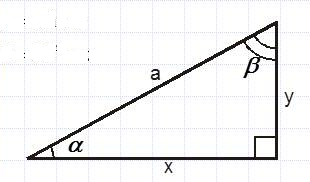 Алгоритм № 3. Дано: Катет и острый угол. 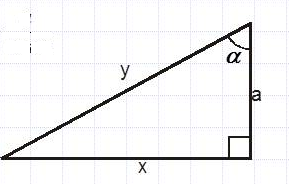 Алгоритм № 4. Дано: Высота опущенная на гипотенузу и острый угол. 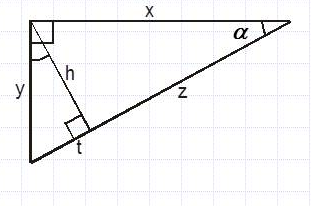 | Взаимопроверка. Самопроверка По образцу (6 баллов) ФО накопительная оценка | Презинтация |