МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»
Кафедра «Информатики»
Лабораторная работа №1

по теме
«Методы решения нелинейных уравнений»

по дисциплине

«Численные методы»

Выполнил: студент гр. БИК2106 Михайлов А.В.

Вариант №13
Проверил: _________


Москва, 2022 г.
1. Пример выполнения задания с использованием математического пакета MathCad

• 
  Решить уравнение: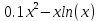
  
• 
  Метод решения нелинейных уравнений – половинного деления
  

Этап отделения корней.

Используем для этого математический пакет MathCad. Отделение корней произведем графическим методом, так и аналитически




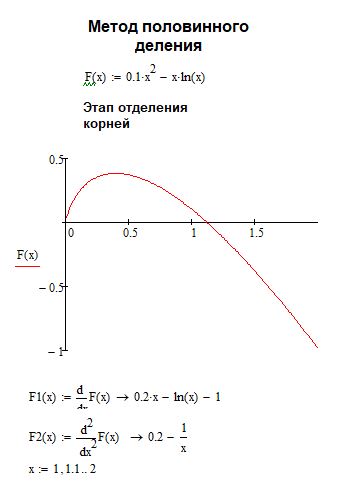
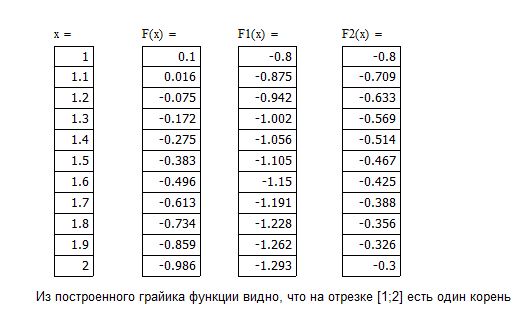
Рисунок 1 - Графическое и аналитическое отделение корней уравнения.

Из построенного графика функции f(x) видно, что на отрезке [1;2] есть один корень.

Этап уточнения корня методом половинного деления

1. 
   Исследование задания
   

• 
  Метод половинного деления сходится, если на выбранном отрезке отделен один корень. Так как на отрезке [1;2] функция
  

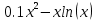меняет знак ( 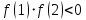, а также монотонна f′(x)<0, то условие сходимости выполняется.

• 
  Выберем за начальное приближение середину отрезка
  

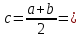1.5

• 
  Для оценки погрешности метода половинного деления справедливо условие:
  

---

|bn – an| < ε, т.е. длина отрезка, полученного на n-ом шаге, должна быть меньше заданной точности, где ε – данная погрешность

Результаты «ручного расчета» трех итераций



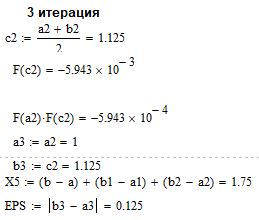
Рисунок 2 - Три итерации метода половинного деления
Результаты вычислений занесём в таблицу 1, которая показана ниже:
Таблица 1

n	an	bn	F(an)	F(bn)	(an+bn)/2	F[(an+bn)/2]	bn-an
0	1	2	0.1	-0.986	1.5	-0.383	1
1	1	1.5	0.1	-0.383	1.25	-0.123	0.5
2	1	1.25	0.1	-0.123	1.125	-0.005943	0.25
3	1	1.125	0.1	-0.005943	1.063	0.048	0.125

После трех итераций приближение к корню – середина отрезка [a3; b3] – X3=1.75

Оценка погрешности результата после трех итераций: R = | b3 – a3 | = 0.125.

Это значит, что X3 отличается от неизвестного точного значения корня не больше, чем на величину R = 0.125.
Пример выполнения задания с использованием языка программирования JavaScript

• 
  Решить уравнение:
  
• 
  Метод решения нелинейных уравнений – метод хорд
  

Для получения решения уравнения методом хорд воспользуемся следующей рекуррентной формулой:



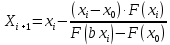
Результат работы программы показан на рисунке 3



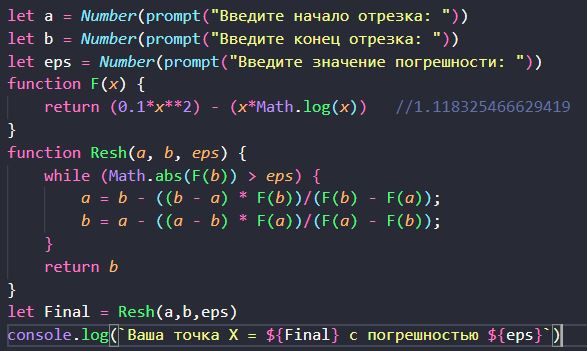
Рисунок 3 – Результат работы программного кода

---

В начале выполнения программного кода выбирается отрезок функции [a; b] и погрешность (eps). После идёт процесс нахождения точки с помощью заданной формулы, после чего результат программного кода выводится в консоль.

---

Смотрите также файлы

• Основы теории электромагнитных полей и волн.docx

• Лабораторная работа 1 Электрическая цепь Цель построить и изучить простую электрическую цепь.docx

• Методические рекомендации к теме 13. Социальноэкономическое.pdf

• Организационноэкономическая характеристика базы практики.docx

• Номинальный управляющий ток, мА.docx