Файл: Определение функции одной переменной. Области определения и значений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Определение функции одной переменной. Области определения и значений.
Пусть задано некоторое множество Х состоящее из элементов х и которое будет называться областью определения функции. Пусть область значений функции есть множество У, состоящих из у. Говорят, что на множестве Х задана функция, если каждому элементу х по некоторому закону f ставится в соответствии свой один элемент. Если множества Х и У состоят из действительных чисел, то f действительная функция одной действительной переменной. Способы задания функции: аналитический, табличный, графический. Если разным значениям аргумента соответствуют разные значения функции, то функция называется взаимно однозначной. Функция называется возрастающей, если большему значению аргумента соответствует большее значение аргумента. Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции. Функция называется монотонной если она либо возрастает, либо убывает.
-
Элементарные функции и их графики (x, x2, x3, sin x, cos x, tg x, ctg x)
-
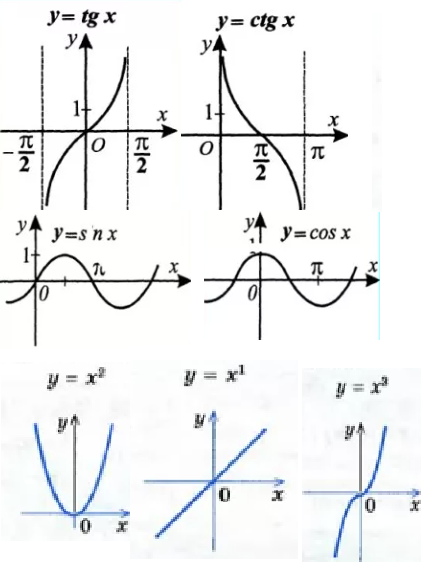
Элементарные функции и их графики (ax, logax, arcsin x, arccos x, arctg x, arcctg x)
-
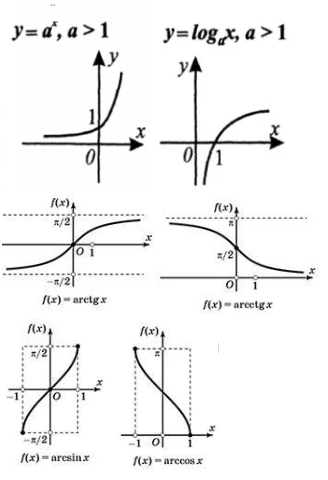
Модуль числа. Свойства модуля.
Абсолютной величиной или модулем действительного числа а называется неотрицательное число |a|, равное числу а, если а>0, и числу –а, если а<0.
Свойства: 1. |a|>=0
-
|a|=|-a|
-
-|a|<=a<=|a|
-
|ab|=|a||b|
-
|a|<=b
-
|a+b| <=|a|+|b|
-
|a-b|>=||a|-|b||
-
Числовая последовательность. Предел последовательности.
Последовательность – функция натурального аргумента: an=f(n), здесь n – номер члена последовательности, an – общий член последовательности. Последовательность а1, а2, а3, … аn обозначают {an}. Элементы, из которых составлена последовательность, называют членами последовательности. Последовательности, членами которых являются числа, называют числовыми. Если члены последовательности {an} начиная с некоторого номера являются приближениями числа а с любой наперед заданной точностью, то число а называют пределом последовательности {an}. Число а называется приделом последовательности {an}, если для каждого E>0 существует натуральное число N такое, что при всех n>N выполняется неравенство |an – a| < E. В этом случае пишут a = lim an или an -> a при n -> бесконечности и говорят, что an сходится к а.
-
Бесконечно малые и бесконечно большие последовательности. Свойства.
Если последовательность {an} сходится к нулю, то она называется бесконечно малой.
∀ ???? > 0 ∃ ????(????) ∈ N : ∀ ???? > ???? |????????| < ????.
Последовательность {an} называют бесконечно большой, если
∀ ???? > 0 ∃ ????(????) ∈ N : ∀ ???? > ???? |????????| > ????.
В этом случае пишут lim an = бесконечность (n стремится к бесконечности)
Последовательность {an} имеет пределом +бесконечность, если
∀ ???? > 0 ∃ ????(????) ∈ N : ∀ ???? > ???? ???????? > Е
Свойства:
-
1/бм = бб
-
1/бб = бм
-
Const*бм = бм
-
Бм +бм = бм
-
f(x) огран. Функция при x->x0 то f(x)бм = бм
-
lim f(x)=A <=> f(x)=A + a(x), а(х) – бм при x->x0
-
Ограниченные и монотонные последовательности. Теорема о «двух милиционерах».
-
Предел функции при x . Графическая интерпретация.
-
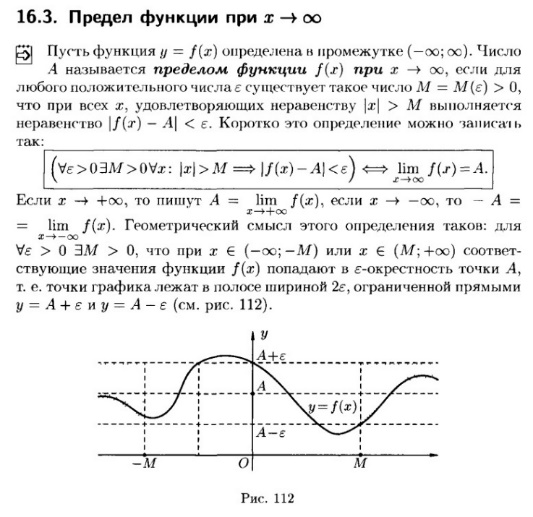
Предел функции при x x0. Графическая интерпретация.
-
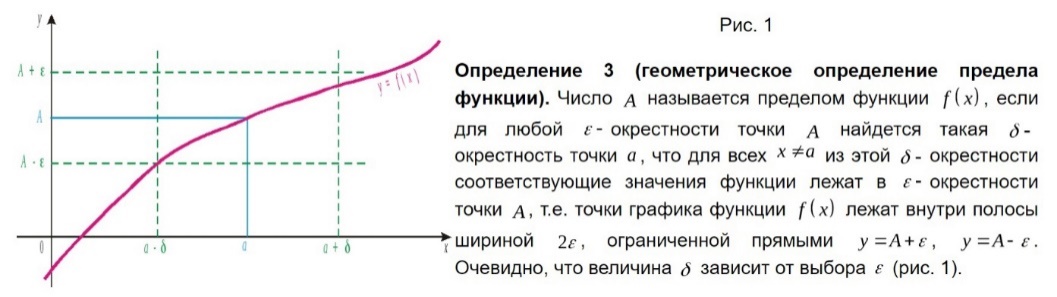
Односторонние пределы. Условие существования предела
-
Бесконечно малые величины. Теорема о связи бесконечно малых величин с пределами функций.
-
Свойства бесконечно малых величин. Сравнение бесконечно малых.
-
Бесконечно большие величины. Свойства бесконечно больших величин. Связь бесконечно малых и бесконечно больших величин.
-
Основные теоремы о пределах (свойства пределов).
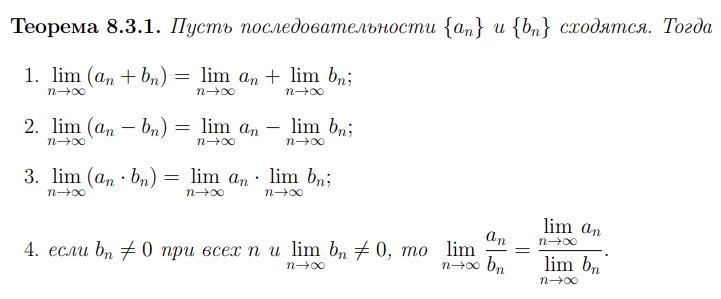
Словами эту теорему обычно формулируют так: предел суммы равен сумме пределов; предел разности равен разности пределов; предел произведения равен произведению пределов; предел частного равен частному пределов. В последнем случае, разумеется, имеется в виду, что ни члены последовательности делителей, ни её предел не равны нулю.
-
Замечательные пределы.
Первый замечательный предел
Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е.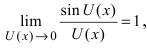 
и называется первым замечательным пределом.
Вторым замечательным пределом называется предельное равенство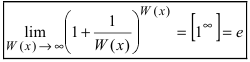
(первая форма)
или
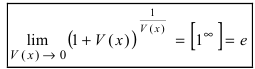(вторая форма).
Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены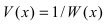 
с учетом теоремы о связи бесконечно большой функции с бесконечно малой функцией.
Замечание: Наличие неопределенности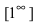 
указывает на второй замечательный предел, т.е. если пределы функций 
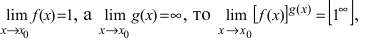что указывает на второй замечательный предел.
-
Эквивалентные бесконечно малые. Доказательство для: ln (1 + x)
x, tg x
x, sin x
-
Определение функции одной переменной. Области определения и значений.
Пусть задано некоторое множество Х состоящее из элементов х и которое будет называться областью определения функции. Пусть область значений функции есть множество У, состоящих из у. Говорят, что на множестве Х задана функция, если каждому элементу х по некоторому закону f ставится в соответствии свой один элемент. Если множества Х и У состоят из действительных чисел, то f действительная функция одной действительной переменной. Способы задания функции: аналитический, табличный, графический. Если разным значениям аргумента соответствуют разные значения функции, то функция называется взаимно однозначной. Функция называется возрастающей, если большему значению аргумента соответствует большее значение аргумента. Функция называется убывающей, если большему значению аргумента соответствует меньшее значение функции. Функция называется монотонной если она либо возрастает, либо убывает.
-
Элементарные функции и их графики (x, x2, x3, sin x, cos x, tg x, ctg x)
-
Элементарные функции и их графики (ax, logax, arcsin x, arccos x, arctg x, arcctg x)
-
Модуль числа. Свойства модуля.
Абсолютной величиной или модулем действительного числа а называется неотрицательное число |a|, равное числу а, если а>0, и числу –а, если а<0.
Свойства: 1. |a|>=0
-
|a|=|-a|
-
-|a|<=a<=|a|
-
|ab|=|a||b|
-
|a|<=b
-
|a+b| <=|a|+|b|
-
|a-b|>=||a|-|b||
-
Числовая последовательность. Предел последовательности.
Последовательность – функция натурального аргумента: an=f(n), здесь n – номер члена последовательности, an – общий член последовательности. Последовательность а1, а2, а3, … аn обозначают {an}. Элементы, из которых составлена последовательность, называют членами последовательности. Последовательности, членами которых являются числа, называют числовыми. Если члены последовательности {an} начиная с некоторого номера являются приближениями числа а с любой наперед заданной точностью, то число а называют пределом последовательности {an}. Число а называется приделом последовательности {an}, если для каждого E>0 существует натуральное число N такое, что при всех n>N выполняется неравенство |an – a| < E. В этом случае пишут a = lim an или an -> a при n -> бесконечности и говорят, что an сходится к а.
-
Бесконечно малые и бесконечно большие последовательности. Свойства.
Если последовательность {an} сходится к нулю, то она называется бесконечно малой.
∀ ???? > 0 ∃ ????(????) ∈ N : ∀ ???? > ???? |????????| < ????.
Последовательность {an} называют бесконечно большой, если
∀ ???? > 0 ∃ ????(????) ∈ N : ∀ ???? > ???? |????????| > ????.
В этом случае пишут lim an = бесконечность (n стремится к бесконечности)
Последовательность {an} имеет пределом +бесконечность, если
∀ ???? > 0 ∃ ????(????) ∈ N : ∀ ???? > ???? ???????? > Е
Свойства:
-
1/бм = бб
-
1/бб = бм
-
Const*бм = бм
-
Бм +бм = бм
-
f(x) огран. Функция при x->x0 то f(x)бм = бм
-
lim f(x)=A <=> f(x)=A + a(x), а(х) – бм при x->x0
-
Ограниченные и монотонные последовательности. Теорема о «двух милиционерах».
-
Предел функции при x . Графическая интерпретация.
-
Предел функции при x x0. Графическая интерпретация.
-
Односторонние пределы. Условие существования предела
-
Бесконечно малые величины. Теорема о связи бесконечно малых величин с пределами функций.
-
Свойства бесконечно малых величин. Сравнение бесконечно малых.
-
Бесконечно большие величины. Свойства бесконечно больших величин. Связь бесконечно малых и бесконечно больших величин.
-
Основные теоремы о пределах (свойства пределов).
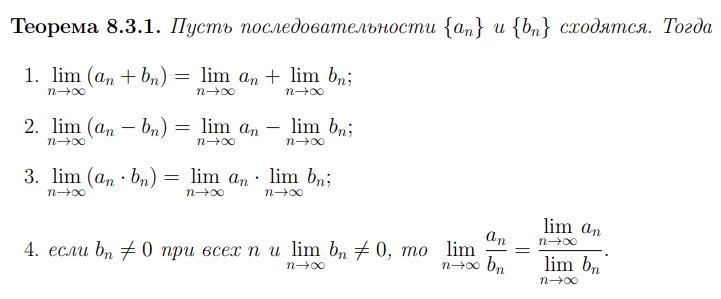
Словами эту теорему обычно формулируют так: предел суммы равен сумме пределов; предел разности равен разности пределов; предел произведения равен произведению пределов; предел частного равен частному пределов. В последнем случае, разумеется, имеется в виду, что ни члены последовательности делителей, ни её предел не равны нулю.
-
Замечательные пределы.
Первый замечательный предел
Определение: Предел отношения синуса какого-либо аргумента к этому аргументу при стремлении аргумента к нулю равен единице, т.е. 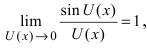и называется первым замечательным пределом.
Вторым замечательным пределом называется предельное равенство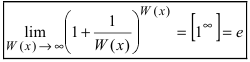 (первая форма)
или
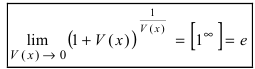(вторая форма).
Замечание: Первая форма второго замечательного предела переходит во вторую с помощью замены 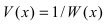с учетом теоремы о связи бесконечно большой функции с бесконечно малой функцией.
Замечание: Наличие неопределенности 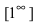указывает на второй замечательный предел, т.е. если пределы функций 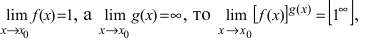что указывает на второй замечательный предел.
-
Эквивалентные бесконечно малые. Доказательство для: ln (1 + x)
x, tg x
Определение функции одной переменной. Области определения и значений.
Элементарные функции и их графики (x, x2, x3, sin x, cos x, tg x, ctg x)
Элементарные функции и их графики (ax, logax, arcsin x, arccos x, arctg x, arcctg x)
Модуль числа. Свойства модуля.
|a|=|-a|
-|a|<=a<=|a|
|ab|=|a||b|
|a|<=b
|a+b| <=|a|+|b|
|a-b|>=||a|-|b||
Числовая последовательность. Предел последовательности.
Бесконечно малые и бесконечно большие последовательности. Свойства.
1/бм = бб
1/бб = бм
Const*бм = бм
Бм +бм = бм
f(x) огран. Функция при x->x0 то f(x)бм = бм
lim f(x)=A <=> f(x)=A + a(x), а(х) – бм при x->x0
Ограниченные и монотонные последовательности. Теорема о «двух милиционерах».
Предел функции при x . Графическая интерпретация.
Предел функции при x x0. Графическая интерпретация.
Односторонние пределы. Условие существования предела
Бесконечно малые величины. Теорема о связи бесконечно малых величин с пределами функций.
Свойства бесконечно малых величин. Сравнение бесконечно малых.
Бесконечно большие величины. Свойства бесконечно больших величин. Связь бесконечно малых и бесконечно больших величин.
Основные теоремы о пределах (свойства пределов).
Замечательные пределы.
Эквивалентные бесконечно малые. Доказательство для: ln (1 + x)
x
-
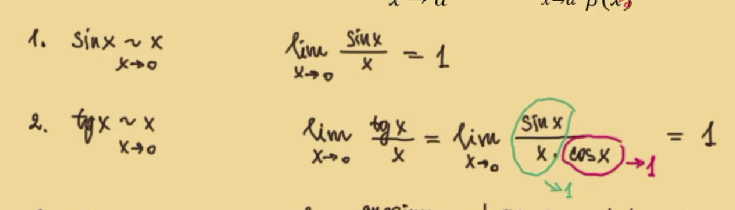
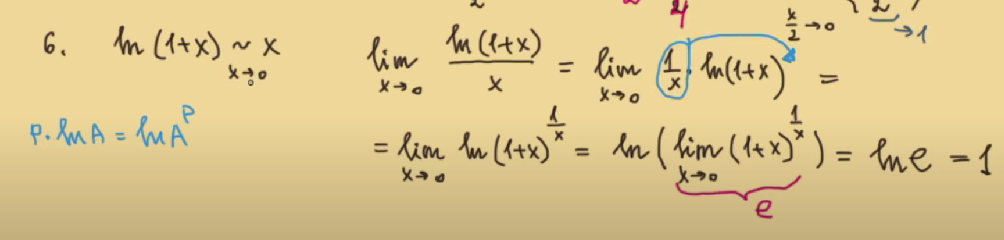
Непрерывность функции в точке. Определение непрерывности функции через приращение.
-
Точка разрыва функции. Классификация точек разрыва.
Если хотя бы один из односторонних пределов
равен бесконечности или не существует, то 
называется точкой разрыва второго рода функции f(x).-
Свойства функций, непрерывных в точке.
-
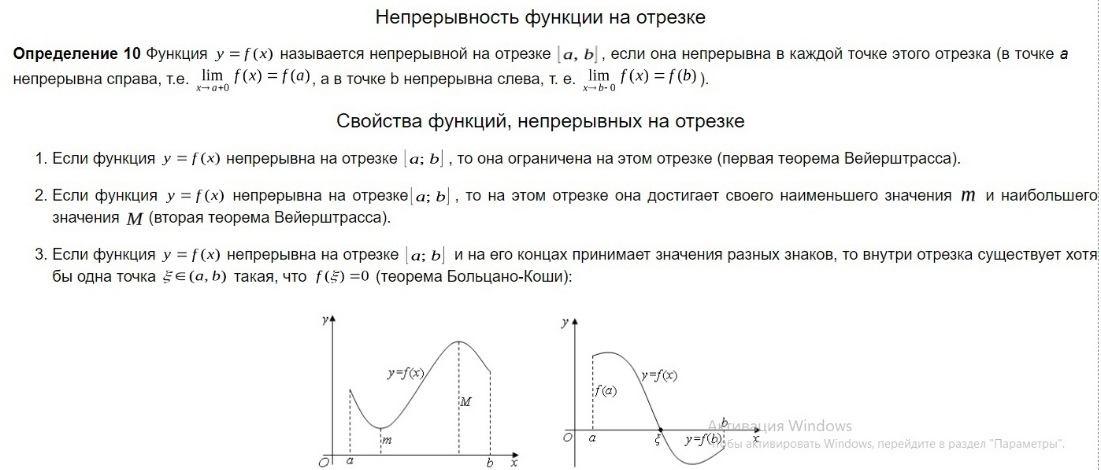
Свойства функций, непрерывных на отрезке (теоремы Вейерштрасса и Больцано-Коши).
-
Производная функции в точке: Геометрический и физический смысл производной. Уравнение касательной к графику функции. -
Физический смысл производной. Левая и правая производные.
-
Зависимость между непрерывностью функции и дифференцируемостью.
Если функция дифференцируема в некоторой точке, то в этой точке функция непрерывна. Заметим, что обратное утверждение неверно: непрерывная функция может не иметь производной. Например, функция
непрерывна при
, но не дифференцируема для этого значения, так как в точке графика функции не существует касательной. Таким образом, непрерывность функции необходимое, но не достаточное условие дифференцируемости функции.-
Схема вычисления производной. Основные правила дифференцирования. Производная сложной и обратной функций.
-
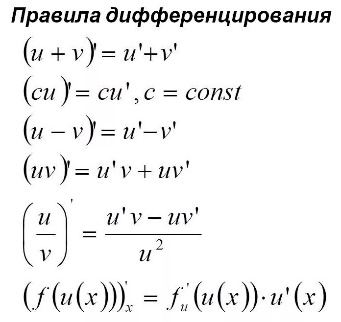
Производная показательно – степенной функции.
-
Производные элементарных функций (таблица производных).
-
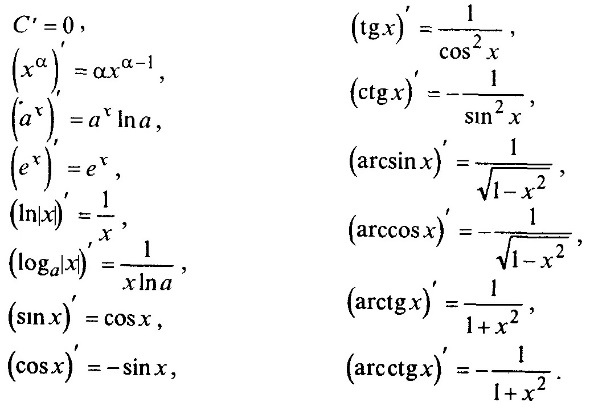
Дифференциал функции. Геометрический смысл дифференциала.
-
Свойства дифференциала. Инвариантность формы первого дифференциала.
-
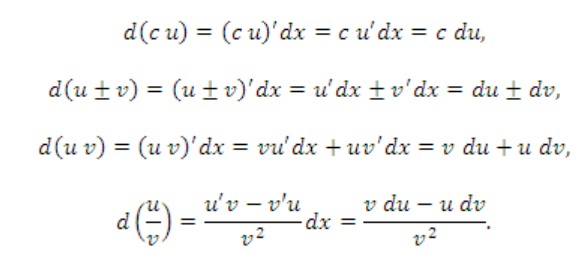
Приближенные вычисления при помощи дифференциала.
-
Производные и дифференциалы высших порядков.
-
Производные параметрически и неявно заданных функций.
Уравнение Fx, y 0 , неразрешенное относительно y , задает неявную функцию y аргумента x .
-
Теоремы Ферма и Ролля
-
Теорема Лагранжа. Геометрическая интерпретация.
-
Раскрытие неопределенностей. Правило Лопиталя.
-
Формула Тейлора. Запись формулы Тейлора через приращения.
-
Остаточный член в формах Лагранжа и Пеано.
-
Формула Маклорена.
Формулой Маклорена называют формулу Тейлора при а=0
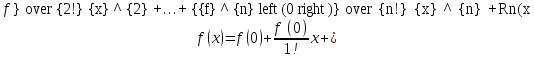
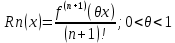
38. Разложение элементарных функций в ряд Маклорена
.
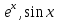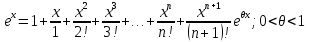
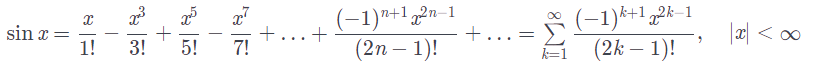
39. Разложение элементарных функций в ряд Маклорена:
.
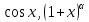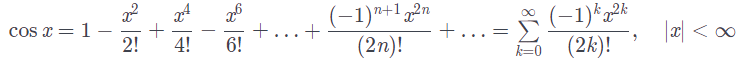
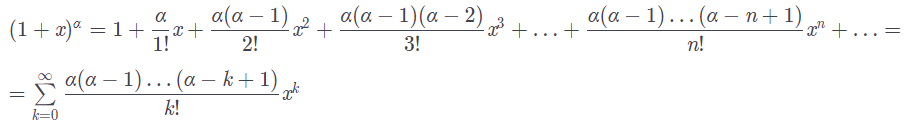
40. Возрастание и убывание функции.
Определение возрастающей функции.
Функция y=f(x) возрастает на интервале X, если для любых
и 
выполняется неравенство 
. Другими словами – большему значению аргумента соответствует большее значение функции.Определение убывающей функции.
Функция y=f(x) убывает на интервале X, если для любых
и выполняется неравенство 
. Другими словами – большему значению аргумента соответствует меньшее значение функции.
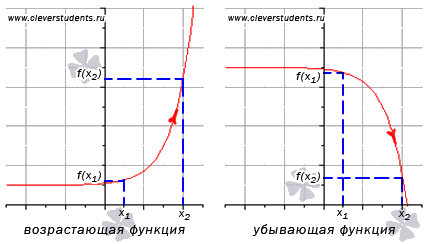
ЗАМЕЧАНИЕ: если функция определена и непрерывна в концах интервала возрастания или убывания (a;b), то есть при x=a и x=b, то эти точки включаются в промежуток возрастания или убывания. Это не противоречит определениям возрастающей и убывающей функции на промежутке X.
41. Точки экстремума.