Файл: Определение функции одной переменной. Области определения и значений.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 04.12.2023
Просмотров: 25
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Точку
называют точкой максимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство 
. Значение функции в точке максимума называют максимумом функции и обозначают 
.Точку
называют точкой минимума функции y=f(x), если для всех x из ее окрестности справедливо неравенство 
. Значение функции в точке минимума называют минимумом функции и обозначают 
.Под окрестностью точки
понимают интервал 
, где 
- достаточно малое положительное число.Т
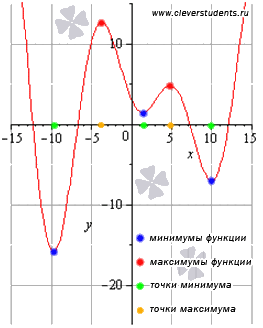
очки минимума и максимума называют точками экстремума, а значения функции, соответствующие точкам экстремума, называют экстремумами функции.
42. Критические точки.
43. Достаточные условия экстремума.
44. Исследование функций и помощью производных высших порядков.
45. Выпуклость и вогнутость кривой.
46. Точки перегиба.
*47. Асимптоты.
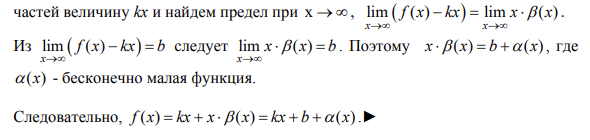
48. Схема исследования функций.
-
Область существования функции (это понятие включает в себя и область значения и область определения функции) -
Точки разрыва (Если они имеются) -
Интервалы возрастания и убывания -
Точки максимума и минимума -
Максимальное и минимальное значение функции на её области определения -
Область выпуклости и вогнутости. -
Точки перегиба (Если они есть) -
Асимптоты (Если они есть) -
Построение графика
49. Векторная функция скалярного аргумента.
где x(t), y(t), z(t) - координаты векторной функции r(t)
50. Уравнение касательной к кривой.
51. Свойства производной векторной функции скалярного аргумента.
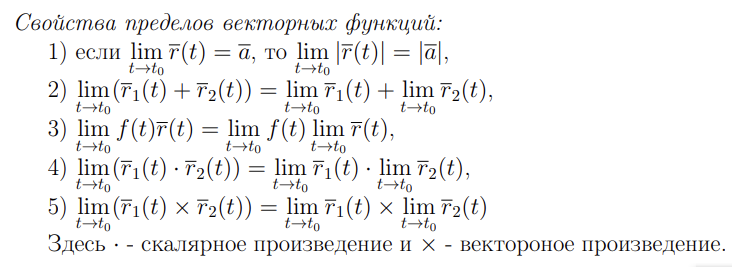
52. Уравнение нормальной плоскости.
53. Параметрическое задание функции.
54. Окружность.
55. Эллипс.
56. Циклоида.
57. Астроида.
58. Производная функции, заданной параметрически.
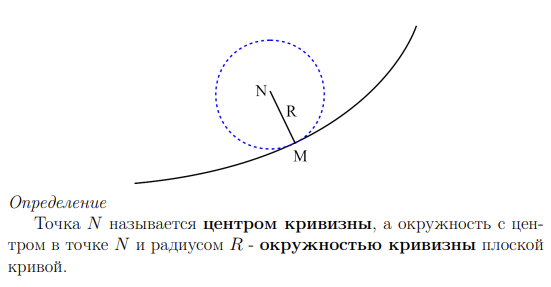
59. Кривизна плоской кривой. Средняя кривизна. Радиус кривизны. Центр и круг кривизны.
60. Угол смежности.
62. Кривизна дуги в точке.
65. Эволюта и эвольвента. В вк
66. Свойства эволюты. В вк
67. Кривизна пространственной кривой.
68. Годограф.
69. Главная нормаль.
70. Вектор и радиус кривизны.
71. Кручение кривой.