Файл: Лабораторная работа 1 Исследование устойчивости системы автоматического регулирования скорости вращения двигателя с помощью критерия Гурвица.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 46
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Методические указания по выполнению лабораторных работ.
Лабораторная работа № 1
«Исследование устойчивости системы автоматического регулирования скорости вращения двигателя с помощью критерия Гурвица»
Дано: Структурная схема системы автоматического регулирования скорости вращения двигателя (Рисунок 1.)
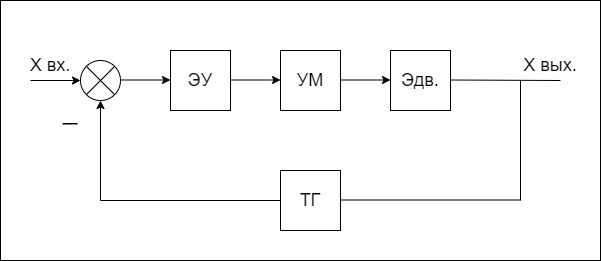
Рисунок 1 «Схема вращения двигателя».
Кэу(Р)=К1
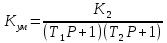
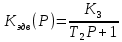
Ктг (Р)=К4
ТГ- тахогенератор
Т1=0,1
Т2=0,2
Т3=0,01
Задание: на основании заданных передаточных функций элементов, необходимо рассчитать критический коэффициент усиления разомкнутой системы ( Ккр) и провести моделирование системы с помощью программы Classic, при различных значениях коэффициентов усиления разомкнутой системы.
Для расчета критического коэффициента усиления разомкнутой системы воспользуемся критерием Гурвица, который определил не только условие устойчивости системы, но и условия нахождения системы на границах устойчивости. Система находится на границе устойчивости если предпоследний диагональный минор определителя Гурвица равен нулю. Граница устойчивости соответствует критическому значению коэффициента усиления разомкнутой системы.
Для получения коэффициентов определителя необходимо знать характеристическое уравнение данной системы. Оно находится следующим образом. Сначала используя формулы для различных соединений звеньев определить общую передаточную функцию замкнутой системы.
Существуют следующие звенья:
1) Электронный усилитель (ЭУ)
2) Электромашинный усилитель (УМ – усилитель мощности)
3) Электродвигатель (Эдв)
Так как они соединены последовательно и их можно заменить одной передаточной функцией:
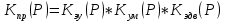
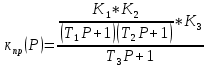
К прямой цепи от (Р) и ТГ (ТГ-тахогенератор) соединены с обратной связью и К общее равно:
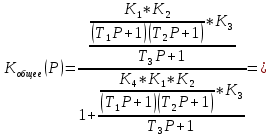
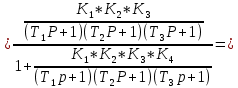
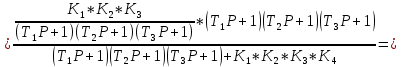
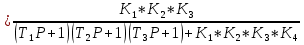
Преобразуем это выражение к виду:
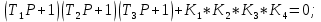
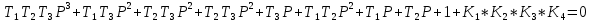
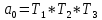
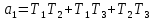
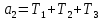
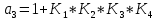
Δ=
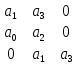
По свойству любой передаточной функции её знаменатель является характеристическим полиномом и, следовательно, дальше можно подставлять значения а0, а1, а2, а3 в предпоследний диагональ деминор и приравнивать его нулю. В итоге получим уравнение, в котором одно неизвестное К (разомкнутая система) = К1*К2*К3*К4. Это и является критическим коэффициентом усиления.
Далее необходимо смоделировать эту систему для удобства моделирования передаточную функцию К электромагнитный усилитель от П представим в виде произведения:
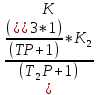
Таким образом в модели прямой цепи будет 4 звена и в обратной связи 1 звено. Classic является свободно распространяемой программой, которую можно скачать с интернета. Принцип моделирования сначала набирается структурная схема в которой в первую очередь набираются звенья прямой цепи и ниже обратной связи, затем используя команду F5 производится соединения звеньев при этом первое звено назначают входом последнее в прямой цепи выходом . В первом звене сигнал обратной связи должен быть с минусом, так как главная обратная связь отрицательная, затем для каждого элемента вводится соответствующая передаточная функция.
Далее дается команда расчет характеристики. Первое моделирование производится при общим коэффициенте усиления разомкнутой системы = 1. При этом необходимо оценить вид переходного процесса (сходящиеся монотонной, колебательной и т.д.) и корни характеристического уравнения. По ним определяется также устойчивость системы. Далее все повторяется при К общ = 12, затем 20. Затем К критическое и больше К критического.
В отчете представляются теоретическая часть расчетная, скрины для всех коэффициентов усиления разомкнутой системы и комментарии к ним. Титульный лист скачивается с официального сайта СПбГУТ.
Лабораторная работа №2
«Исследование устойчивости системы автоматического регулирования скорости вращения двигателя по критерию Найквиста»
Дано: исследуем ту же систему, что и в работе № 1. Теоретическая часть также полностью совпадает с предыдущей работой, поэтому её можно не приводить, а только ссылаться на неё.
В этой работе используется критерий Найквиста — это частотный критерий, который позволяет оценить устойчивость замкнутой системы по частотным характеристикам разомкнутой системы.
В качестве исходного берется рассчитанная в работе №1 значение К критического. Моделирование производится при тех же значениях коэффициентов усиления разомкнутой системы что и в работе №1.
Критерий Найквиста формулируется так:
Если разомкнутая система устойчива, то для устойчивости замкнутой системы необходимо, чтобы АФЧХ (Амплитудно-фазовая частотная характеристика) разомкнутой системы не охватывало точку с координатами (-1,0 или йод 0) Этот же критерий может использовать и логарифмические частотные характеристики. И тогда условием устойчивости будет следующее: система устойчива если, при частоте, когда фазовая характеристика достигает значения -180 градусов. Амплитудная логарифмическая характеристика находится ниже горизонтальной оси (абсцисса)
Таким образом при моделировании необходимо систему разомкнуть (удалить связь со звена обратной связи к первому звену) Далее выставить необходимые коэффициенты усиления нажать расчет характеристики и 1 по виду переходного процесса и корням убедиться в устойчивости разомкнутой системы. Далее на АФЧХ (АФХ в классике) отметить курсором значения координат в точке пересечения с вещественной осью. Снять скрин. Далее то же самое сделать с логарифмическими характеристиками подведя курсор к значению фазовой характеристике – 180 градусов. Скрин.
Задача: представить все скрины для тех же что и в лабораторной работе №1 коэффициентов разомкнутой системы с соответствующими комментариями. В теоретической части привести формулировку определения устойчивости по критерию Найквиста.
Лабораторная работа №3
«Коррекция автоматических систем с помощью обратной связью»
Дано: одной из причин неустойчивости является инерционность элементов, входящих в нее, поэтому возникает первая мысль возможно ли уменьшить инерционность этих элементов, то есть уменьшить постоянную времени. Рассмотрим такую возможность на примере инерционного звена первого порядка. Передаточная функция такого звена
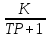. Охватим это звено обратной связью, возможно 2 варианта обратной связи: 1)Жесткая обратная связь, когда Коб св.(Р)=Коб св.
2)Гибкая обратная связь, когда Коб св.(Р)=Коб св.*Р
Задача: первое что нужно сделать написать общее выражение соединения инерционного звена 1 порядка с обратной связью. При этом обратная связь может быть как отрицательной, так и положительной. В результате охвата обратной связи. Мы получим снова инерционное звено 1 порядка возможно с другим коэффициентом усиления и другой постоянной времени. В работе задается исходное значение К = 10 и Т = 10.
Необходимо рассчитать какой должно быть значение К обр. связи и знак обратной связи отдельно для жесткой обратной связи и для гибкой обратной связи. В случае, если уменьшение постоянной времени приведет к изменению коэффициента усиления. Необходимо добавить к общей схеме усилитель, который вернет общий коэффициент усиления к исходному значению.
Определение постоянных времени при моделировании производится по переходному процессу помня, что переходный процесс достигает 0,95 установившегося значения за время 3Т (3 постоянных времен)
Моделирование производится в той же системе Classic. При этом исходному блоку присваивается одновременно статус входа и выхода.
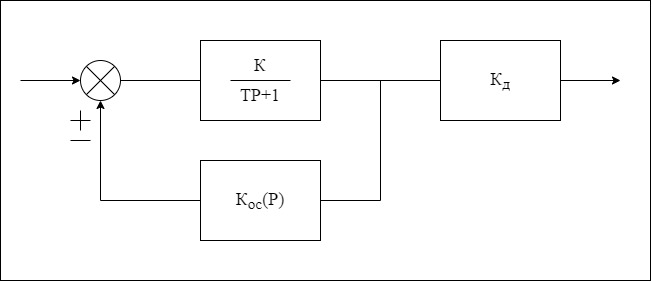
Рисунок 2 «Схема системы».
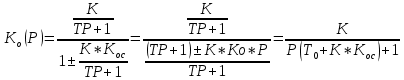
Лабораторная работа № 4
«Моделирование типовых динамических звеньев»
Дано: моделируется следующие звенья:
1)Инерционное звено 1 порядка
2)Звенья 2 порядка,
При ρ больше 1 (А периодическое звено)
При ρ больше 0, меньше 1 (колебательное звено)
При ρ равном нулю (консервативное звено)
В теоретической части приводится для каждого звена уравнение, передаточная функция, АФЧХ, логарифмические характеристики, а в результате моделирования приводится переходный процесс, корневая плоскость, частотные характеристики, логарифмически и АФХ.
Лабораторная работа № 5
«Применение коррекции систем с помощью обратной связи для системы регулирования скорости вращения двигателя»
Дано: система регулирования скорости вращения двигателя, рассмотренная в работе №1, при этом предполагается, что коэффициент усиления разомкнутой системы для обеспечения необходимого уровня статической ошибки выше Ккритического. Рассмотрим систему в которой, К разомкнутой системы равно 40.
Задача: в теоретической части следует рассмотреть следующие варианты Т1 и Т2 исходные значения и необходимо найти возможный диапазон Т3, чтобы система была устойчива при К раз системы равной 40. Такой расчет производится на основании критерия Гурвица и расчетов проведенных в работе №1. После получения этого диапазона это звено с Т3 охватывается жесткой обратной связью, которая делает все систему устойчивой. Такая система моделируется и проверяется правильность теоретических расчетов. Аналогично, такая же процедура проводится при условии, что Т1 и Т3 имею исходные значения, а определяется или рассчитывается диапазон возможных значений Т2. И третий вариант, когда Т2 и Т3 остаются исходными, а рассчитывается и моделируется диапазон для Т1.
При моделировании необходимо учесть, что охват жесткой обратной связью уменьшает общий коэффициент усиления разомкнутой системы. Потерю коэффициента усиления можно компенсировать, изменяя коэффициент усиления в любом из звеньев.
Лабораторная работа № 6
«Синтез последовательного корректирующего устройства»
Дано: система, рассмотренная в учебном пособии по ОТУ (основам теории управления) в разделе «Синтез желаемой ЛАХ (логарифмической амплитудной характеристики), там рассмотрен пример, когда заданы следующие требования к качеству переходного процесса («Сигма» σ = 33%) и (Т