ЛАБОРАТОРНАЯ РАБОТА № 8

ОПРЕДЕЛЕНИЕ НАДЕЖНОСТИ ПРОГРАММНОГО ОБЕСПЕЧЕНИЯ ПО РЕЗУЛЬТАТАМ ТЕСТИРОВАНИЯ И ИСПЫТАНИЙ
Цель работы: Оценка надежности программного обеспечения по результатам тестирования и испытаний.

Задачи работы:

1. Изучить модели определения надежности программного обеспечения.

2. Получить практические навыки использования моделей для расчета надежности программного обеспечения.
Сведения из теории
Для количественной оценки показателей надежности программного обеспечения (ПО) используют модели надежности, под которыми понимаются математические модели, построенные для оценки зависимости этих показателей от заранее известных или определенных в ходе выполнения задания параметров. Значения таких параметров либо предполагаются известными, либо могут быть измерены в ходе наблюдений или экспериментального исследования процесса функционирования программного обеспечения.

Модели надежности программного обеспечения можно разделить на аналитические и динамические.

Аналитические модели дают возможность рассчитать количественные показатели надежности, основываясь на данных о поведении программы в процессе тестирования (измеряющие и оценивающие модели). Аналитические модели подразделяются на динамические и статические. В динамических моделях поведение ПО (появление отказов) рассматривается во времени. В статических моделях появление отказов не связывают со временем, а учитывают зависимость количества ошибок либо от числа тестовых прогонов (модели по области ошибок), либо от характеристики входных данных (модели по области данных).

Эмпирические модели базируются на анализе структурных особенностей программ и являются наиболее простыми моделями. Они основаны на анализе накопленной информации о функционировании разработанных программ. Например, считалось, что если в программе на каждые 1000 операторов приходится 10 ошибок, то она пригодна к эксплуатации. По другим данным, уровень надёжности программ считается приемлемым, если на 1000 операторов приходится одна ошибка.

Модель Шумана. Относится к динамическим моделям дискретного времени. Исходные данные для модели Шумана собираются в процессе тестирования ПО в течение фиксированных или случайных временных интервалов. При использовании модели Шумана предполагаются справедливыми следующие допущения:

---

• 
  тестирование проводится в несколько этапов, выявленные на конкретном этапе ошибки регистрируются, но не исправляются;
  
• 
  в конце этапа рассчитываются количественные показатели надежности, исправляются найденные ошибки, корректируются тестовые наборы и проводится следующий этап тестирования;
  
• 
  число ошибок в программе постоянно и в процессе корректировки новые ошибки не вносятся;
  
• 
  до начала тестирования имеется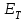 ошибок. В течение времени тестирования τобнаруживается 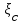ошибок в расчете на одну команду в машинном языке;
  
• 
  общее число машинных команд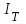 постоянно в рамках этапа тестирования.
  

Базовые понятия модели заимствованы из теории надежности аппаратных средств [6]:

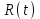­ функция надежности ­ вероятность того, что ни одна ошибка не появится на интервале от 0 до t,

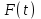­ функция отказов, вероятность того, что ошибка появится на интервале от 0 до t: ,

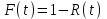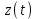­ функция риска, условная вероятность того, что ошибка появится на интервале от 0 до 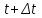, при условии, что до t ошибок не было. Значение функции 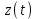пропорционально числу оставшихся в ПО ошибок: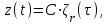

где C ­ некоторая константа, t ­ время работы ПО без отказа, ­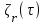 удельное число ошибок на одну машинную команду, оставшихся в системе после времени тестирования τ, вычисляемое как:
.
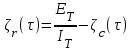Если время работы программы без отказа t отсчитывается от точки

t = 0, а время тестирования τ остается фиксированным, то функция надежности, или вероятность безотказной работы на интервале от 0до t, равна

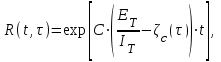
где неизвестными величинами являются начальное количество ошибок

---

и коэффициент пропорциональности C. Для определения этих величин в процессе тестирования собирается информация о времени и количестве ошибок на каждом прогоне, т.е. общее время тестирования τ складывается из времени каждого прогона: 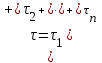. Предполагая, что интенсивность появления ошибок постоянна и равна λ, можно вычислить ее как число ошибок в единицу времени: 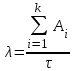, где ­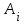 количество ошибок на i-ом прогоне.

Имея данные для двух различных моментов тестирования 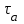и 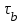, которые выбираются так, чтобы 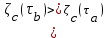, можно записать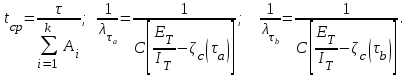

Значения начального количества ошибок и коэффициент пропорциональности C вычисляются как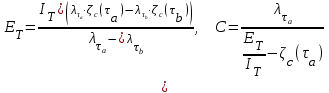


.
Модель Миллса (модель предсказания числа ошибок). Относится к классу аналитических статических моделей. Использование этой модели предполагает необходимость перед началом тестирования искусственно вносить в программу («засорять») некоторое количество известных ошибок.

Тестируя программу в течение некоторого времени, собирают статистику об ошибках. Соотношение 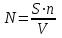дает возможность оценить N – первоначальное число ошибок в программе. В данном соотношении, которое называется формулой Миллса, S– количество искусственно внесенных ошибок, n – число найденных собственных ошибок, V– число обнаруженных к моменту оценки искусственных ошибок.

Мерой доверия к модели является величина C:



,

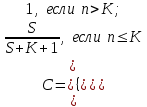
где K ­ количество собственных ошибок в программе.
Простая интуитивная модель.

---

Использование этой модели предполагает проведение тестирования двумя группами программистов (или двумя программистами в зависимости от величины программы) независимо друг от друга и использующими независимые тестовые наборы. В процессе тестирования каждая из групп фиксирует все найденные ею ошибки. При оценке числа оставшихся в программе ошибок результаты тестирования обеих групп собираются и сравниваются.

Пусть N­ неизвестное количество ошибок в программе и первая группа в процессе тестирования обнаружила 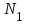ошибок, вторая – 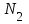, a 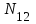– это ошибки, обнаруженные обеими группами (рис. 8.1).

Эффективность тестирования каждой из групп определяется как






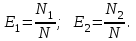
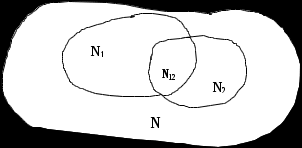
Рис. 8.1. Множество ошибок в программе
Предполагая, что возможность обнаружения всех ошибок одинакова для обеих групп, можно допустить, что если первая группа обнаружила определенное количество всех ошибок, она могла бы определить то же количество любого случайным образом выбранного подмножества. В частности, можно допустить:



.
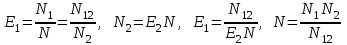
Модель Коркорэна.

Модель Коркорэна относится к статическим моделям надежности ПО, так как в ней не используются параметры времени тестирования. В отличие от двух рассмотренных выше статических моделей, по модели Коркорэна оценивается вероятность безотказного выполнения программы на момент оценки.

Применение модели предполагает знание следующих ее показателей:

• 
  изменяющуюся вероятность отказов для различных источников ошибок и соответственно разную вероятность их исправления;
  
• 
  результаты N испытаний, в которых наблюдается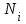 ошибок i-го типа;
  
• 
  вероятности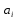 появления ошибок i-го типа.
  

Вероятность безотказного выполнения программы на момент оценки определяется как

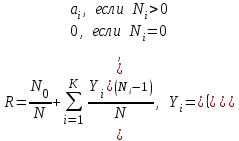
где

---

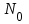
– число безотказных выполнений программы; N – общее число прогонов; K – априори известное число типов ошибок.

Величина вероятности выявления при тестировании ошибки i-го типа должна быть получена на основании данных предшествующего периода функционирования однотипных программных средств.
Контрольные вопросы и задания
1. Приведите классификацию моделей надежности программных средств.

2. Как выполнить оценку надежности программного обеспечения при использовании аналитических моделей?

3. На каких предположениях построена модель «дискретно-понижающая интенсивность проявления ошибок»?

4. На каких допущениях построена модель Шумана?

5. Каким образом определяется надежность программного обеспечения по модели Джелинского-Моранды?

6. В чем заключается различие между статическими и динамическими моделями надежности программных средств?

7. В чем сущность модели Миллса?

8. Каким образом выполняется расчет надежности программного средства с помощью простой интуитивной модели?

9. Каким образом определяется надежность программного обеспечения по модели Коркорэна?

10. В чем сущность интуитивной модели фирмы IBM?

11. Какую модель надежности программы следует применять, если предпринято две попытки тестирования?
Варианты заданий к лабораторной работе
1. Предположим в программе есть три собственные ошибки, внесём ещё шесть случайным образом. В процессе тестирования было найдено пять внесенных ошибок и две собственные. Найти надёжность программы по модели Миллса.

2. В программе есть две собственные ошибки, внесём ещё три случайным образом. В процессе тестирования было найдено две внесенные ошибок и три собственные. Найти надёжность программы по модели Миллса.

3. Предположим в программе есть десять собственных ошибок, внесём ещё пять случайным образом. В процессе тестирования было найдено восемь внесенных ошибок и трисобственные. Найти надёжность программы по модели Миллса.

4. Пусть в программе есть двенадцать собственных ошибок, внесём ещё шесть случайным образом. В процессе тестирования было найдено семь внесенных ошибок и пять собственных. Найти надёжность программы по модели Миллса.

---

Смотрите также файлы

• 2. Ценности и их роль для человека и общества.docx

• Земельное право.docx

• Разгадай ребус.pptx

• Рекомендация по освещению Бессмертного полка в 2023 году.docx

• Многопрофильный колледж профессионального образования дневник производственной практики.docx