Министерство науки и высшего образования Российской Федерации
Федеральное государственное бюджетное образовательное учреждение высшего образования «Владимирский государственный университет имени Александра Григорьевича и Николая Григорьевича Столетовых»(ВлГУ)Кафедра функционального анализа и его приложенийПРАКТИЧЕСКАЯ РАБОТА №1по дисциплине«Разделы математики»На тему:«Матрицы. Действия над матрицами.»Отчет выполнила:Ст. гр. Арх-222Рыжкина А.Д.Вариант 15Отчет проверила:доцент каф. ФАиПКондакова Е.Н.г. Владимир2023 г.Цель работы.Получение и систематизация знаний по теме «Линейная алгебра», а также навыков решения типовых задач.Теория по теме: «Матрицы. Действия над матрицами.»

1. 
   Матрица – таблица чисел (выражений), имеющая «m» строк и «n» столбцов.
   

A_ij– числа, называющиеся матричными элементами. i – нумератор строк, j – нумератор столбцов.M*n – размерность матрицы или ее структура.

2. 
   Матрицы бывают:
   
   1. 
      Матрица-строка – матрица, имеющая 1 строку и n столбцов.
      
   2. 
      Матрица-столбец – матрица, имеющая m строк и 1 столбец.
      
   3. 
      Квадратная матрица – матрица, количество строк и столбцов которой равно.
      
   4. 
      Треугольная матрица – матрица, у которой все элементы, стоящие под главной диагональю равны 0.
      
   5. 
      Диагональная матрица – матрица, все элементы которой за исключением элементов, стоящих на главной диагонали, равны 0.
      
   6. 
      Единичная матрица – диагональная матрица, у которой на главной диагонали все элементы равны 1.
      

3. 
   Действия над матрицами:
   
   1. 
      Суммой (разностью) двух матриц одинаковой структуры А и В называется матрица той же размерности С, элементы которой вычисляются по формуле c_{ij =} a_ij + b_ij.
      
   2. 
      При умножении вещественного числа К на матрицу А все элементы матрица умножаются на это число.
      
   3. 
      Произведением матриц А и В является матрица С, элементы которой вычисляются по формуле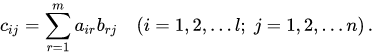
      

---

Перемножать можно лишь те матрицы, для которых количество столбцов первой матрицы совпадает с количеством строк второй матрицы.В общем случае произведение матриц неперестановочно.

4. 
   Определитель, или детерминант квадратной матрицы A размера m×n — это число, ставящееся в соответствие этой матрице A. Обозначается определитель двумя вертикальными черточками |A|∣A∣, греческой буквой Δ, или detA.
   
5. 
   Обратная матрица – матрица А^-1 является обратной для матрицы А (определитель матрицы А не должен быть равен 0), если А^-1*А = А*А^-1 = Е.
   
1. 
   СЛАУ – система линейных алгебраических уравнений.
   

5. 
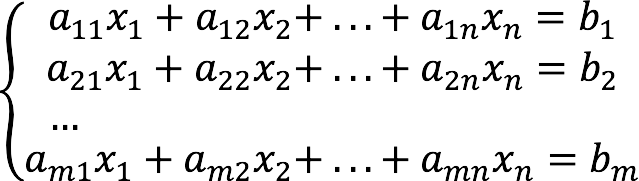
   Методы решения СЛАУ:
   
   1. 
      Метод Крамера.
      
   2. 
      Матричный метод.
      
   3. 
      Метод Гаусса.
      

Онлайн проверка решений задач.Задание 1.

1. 
   2А – 3В
   

2. 
   
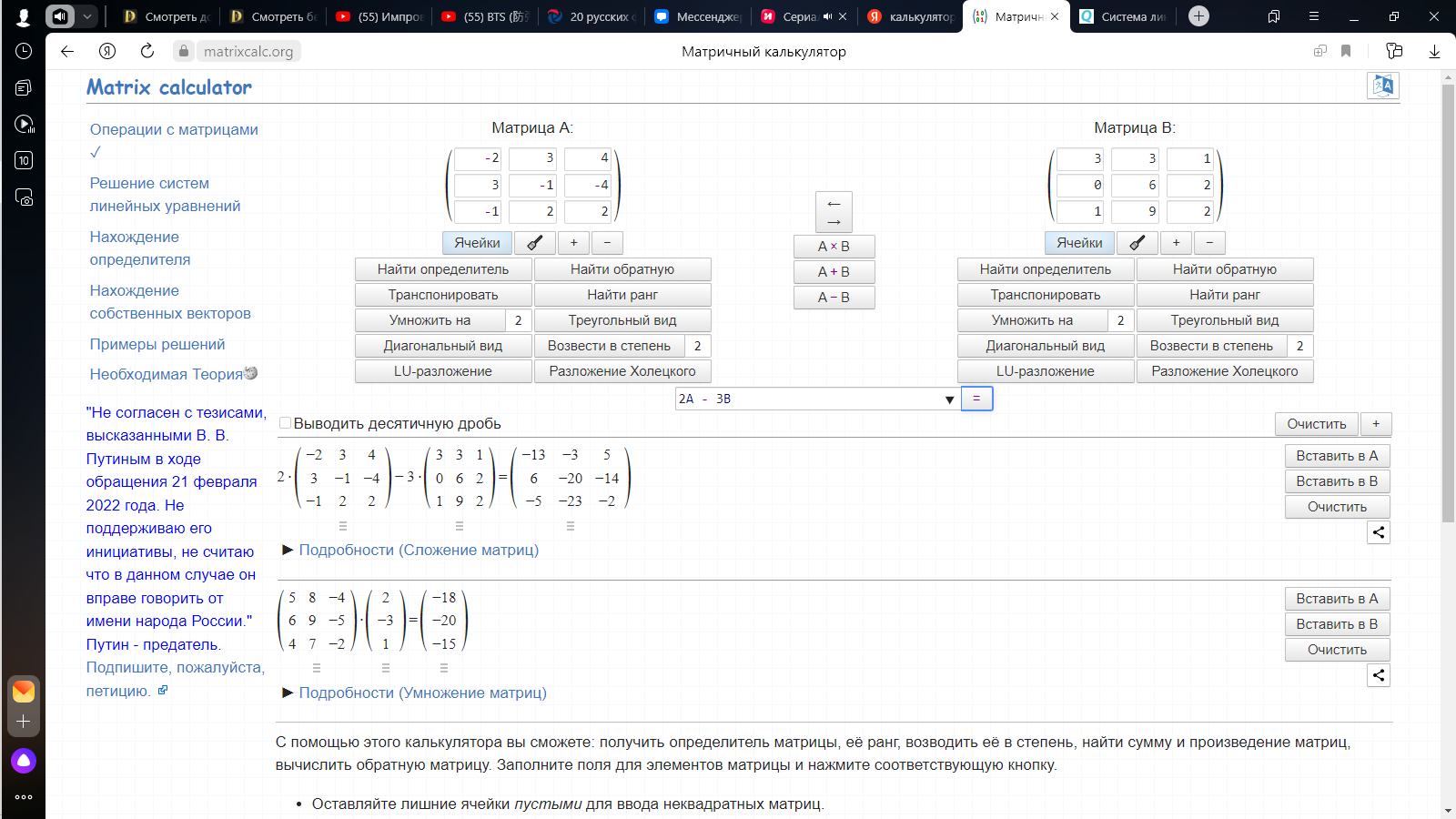
   В*А, А*В. Являются ли матрицы А и В перестановочными?
   

3. 
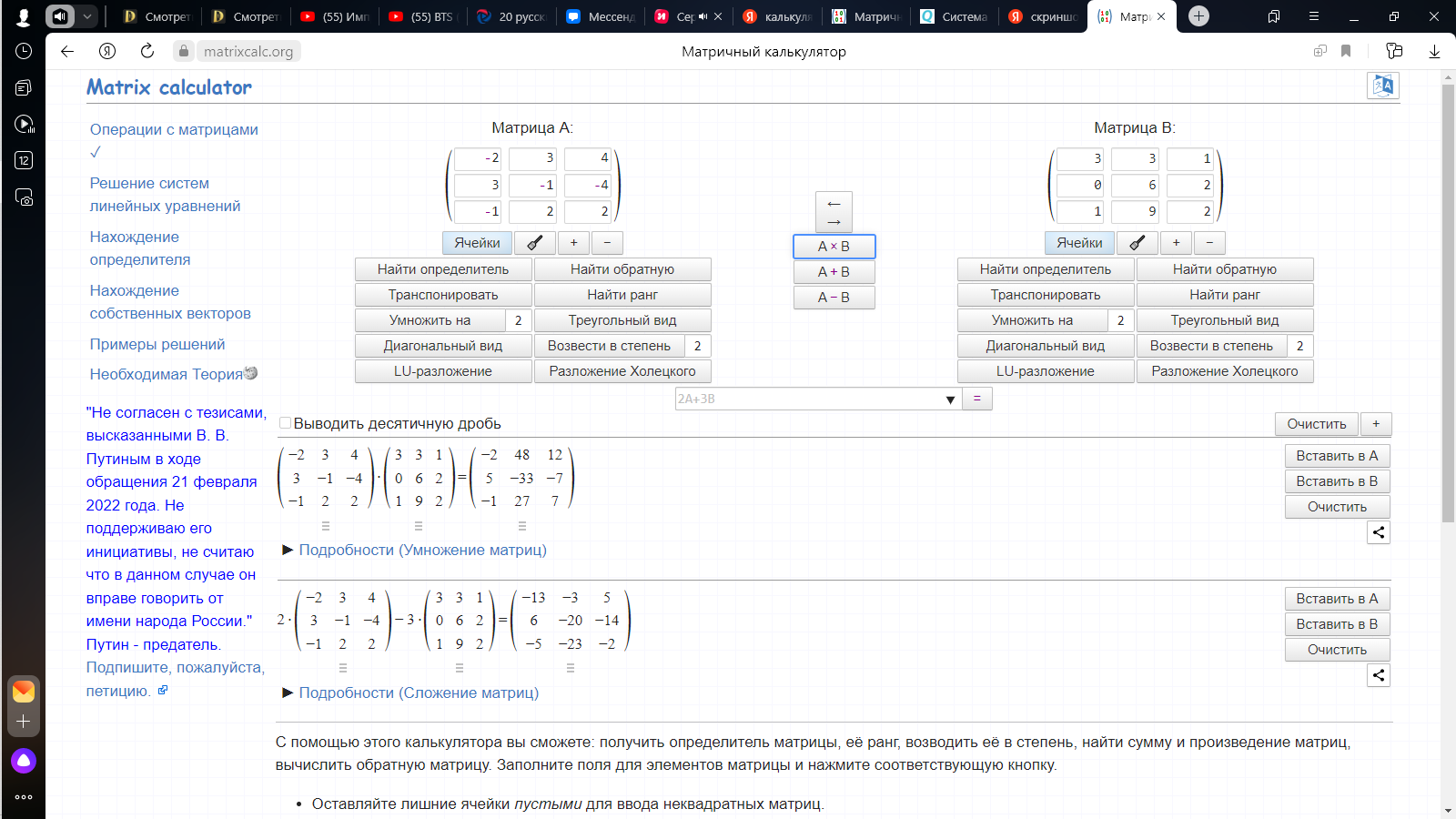
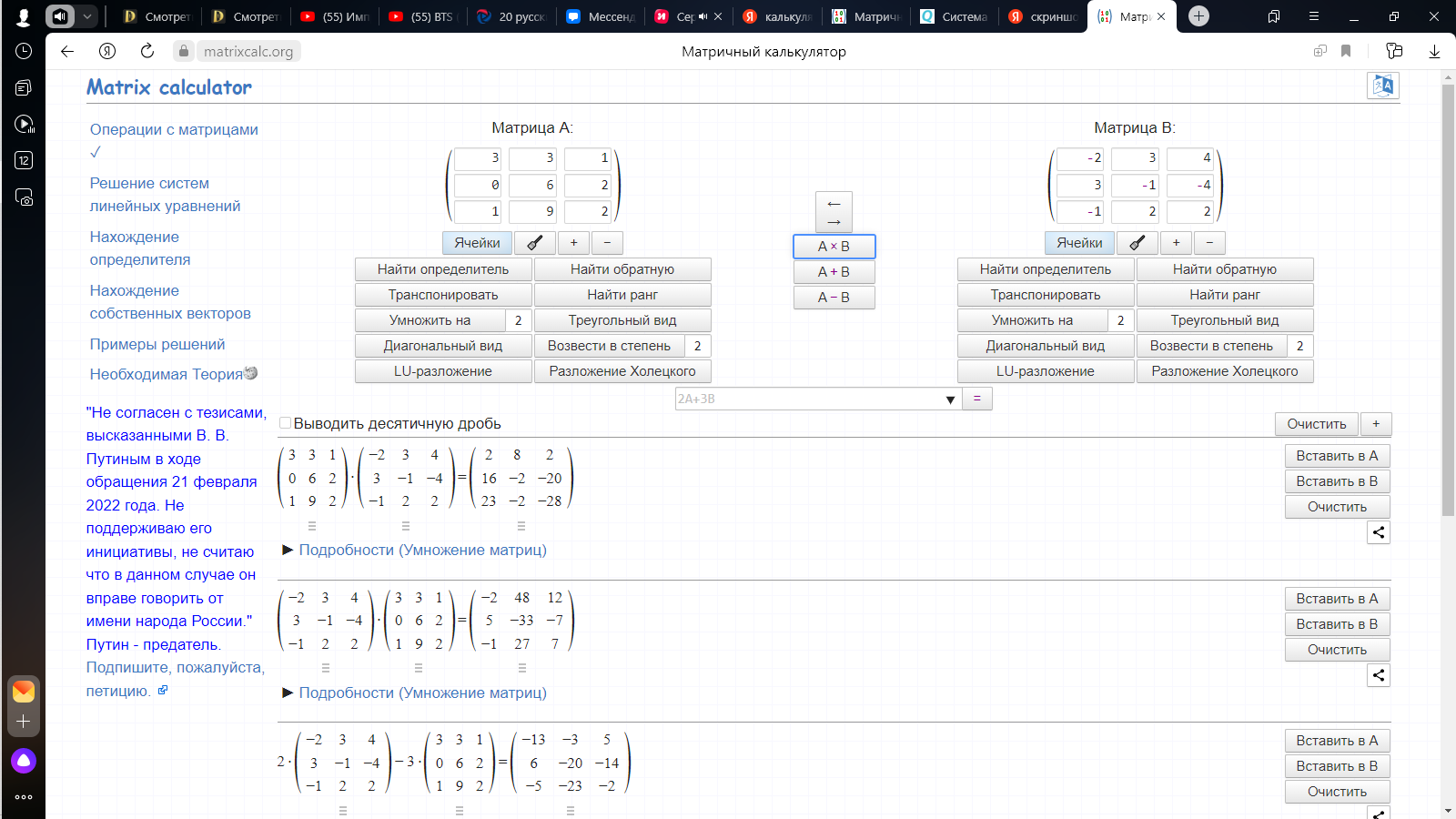
   Вычислить определитель матрицы А.
   

4. 
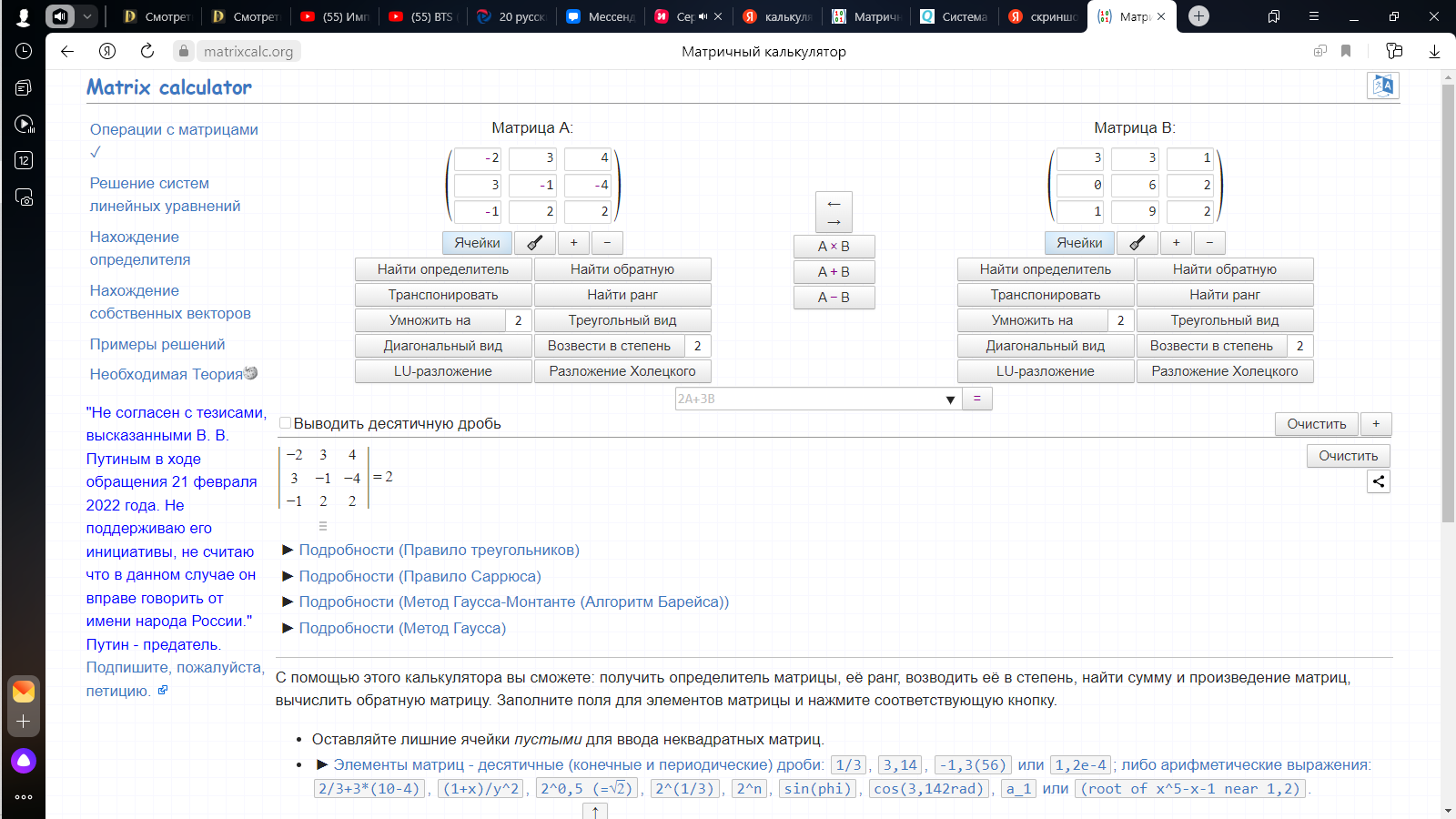
   Обратная матрица В.
   

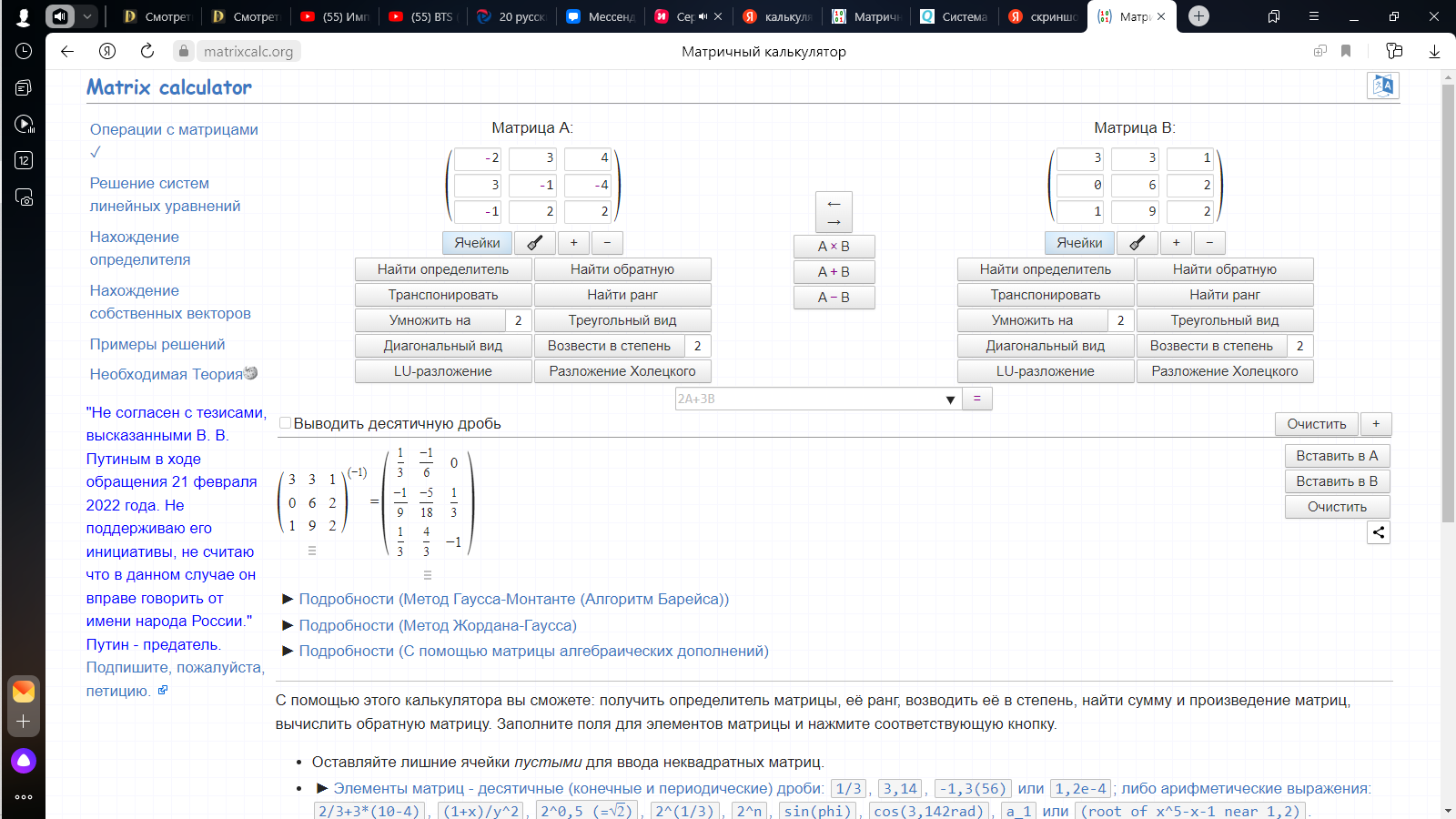
Задание 2. Решение системы линейных уравнений.

1. 
   Методом Крамера.
   

2. 
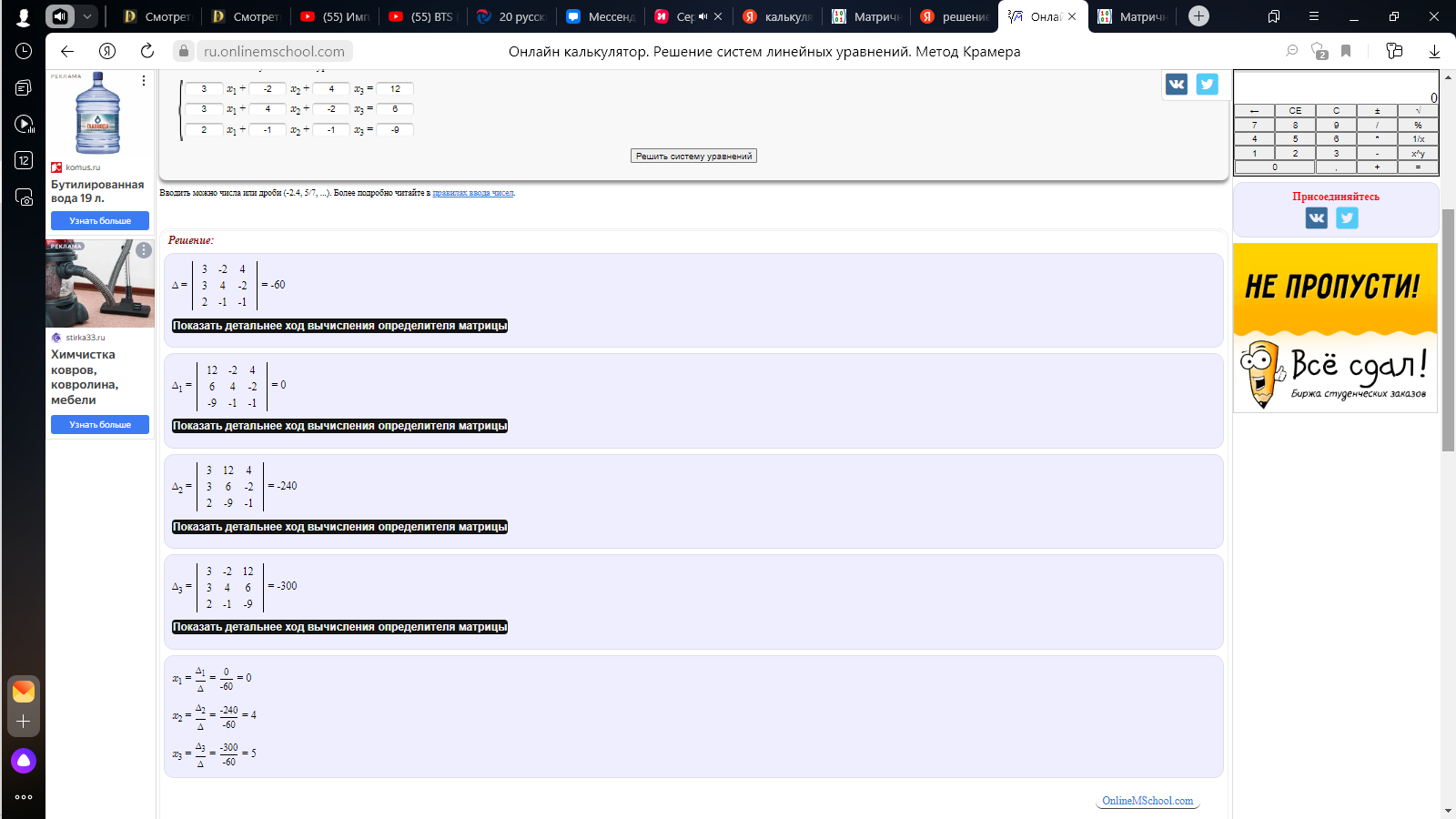
   Матричным методом.
   

3. 
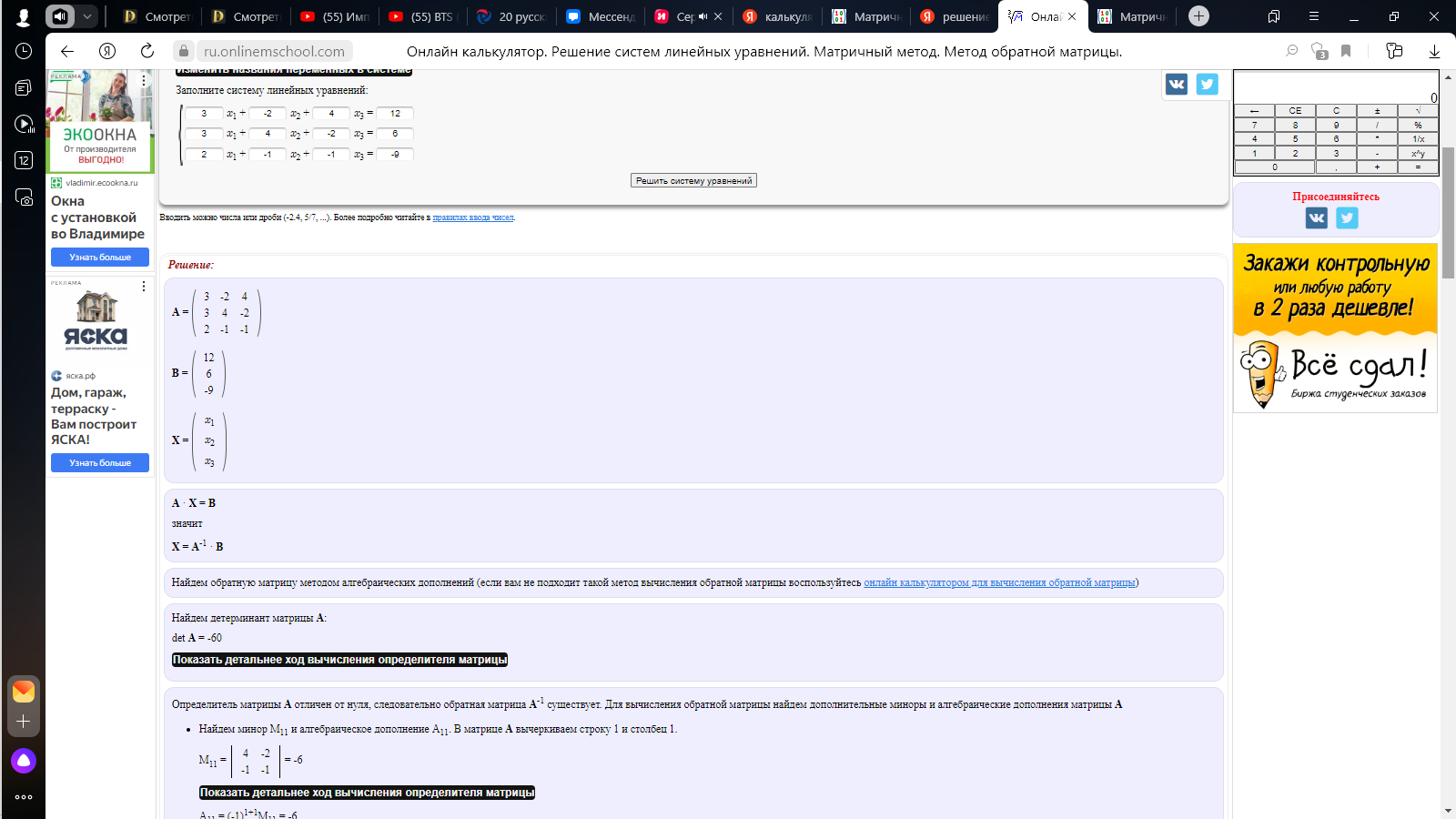
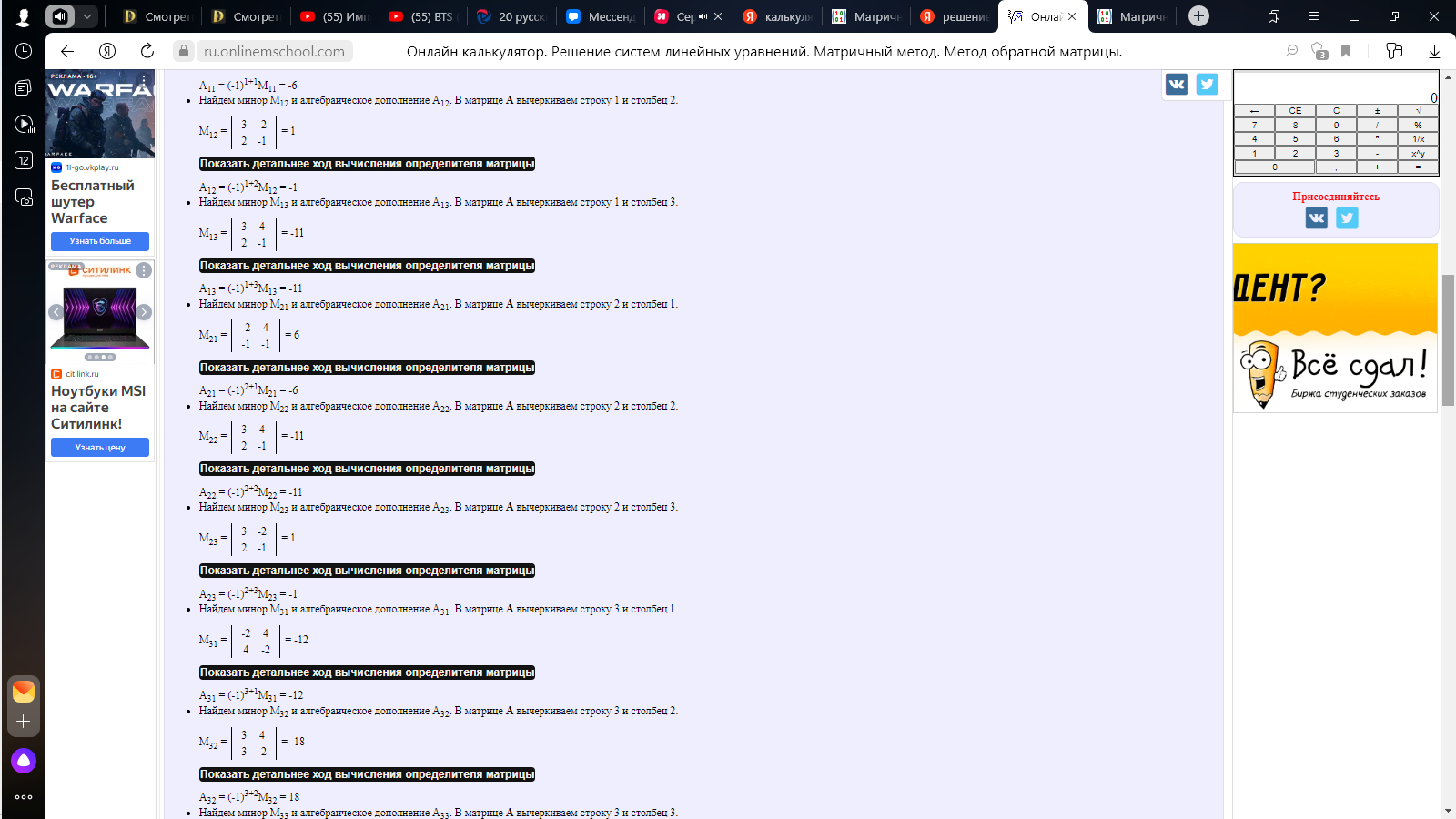
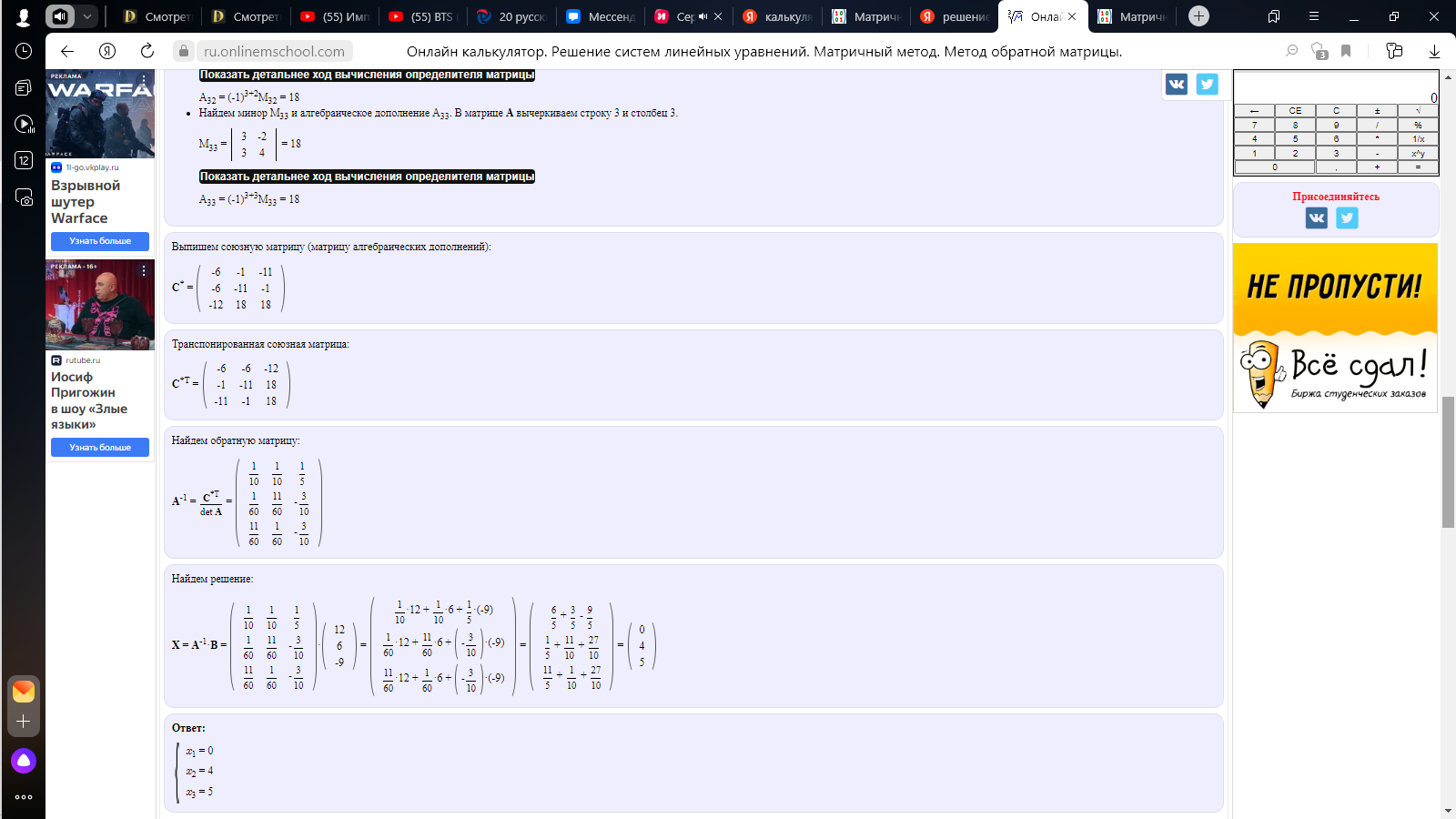
   Методом Гаусса.
   

---

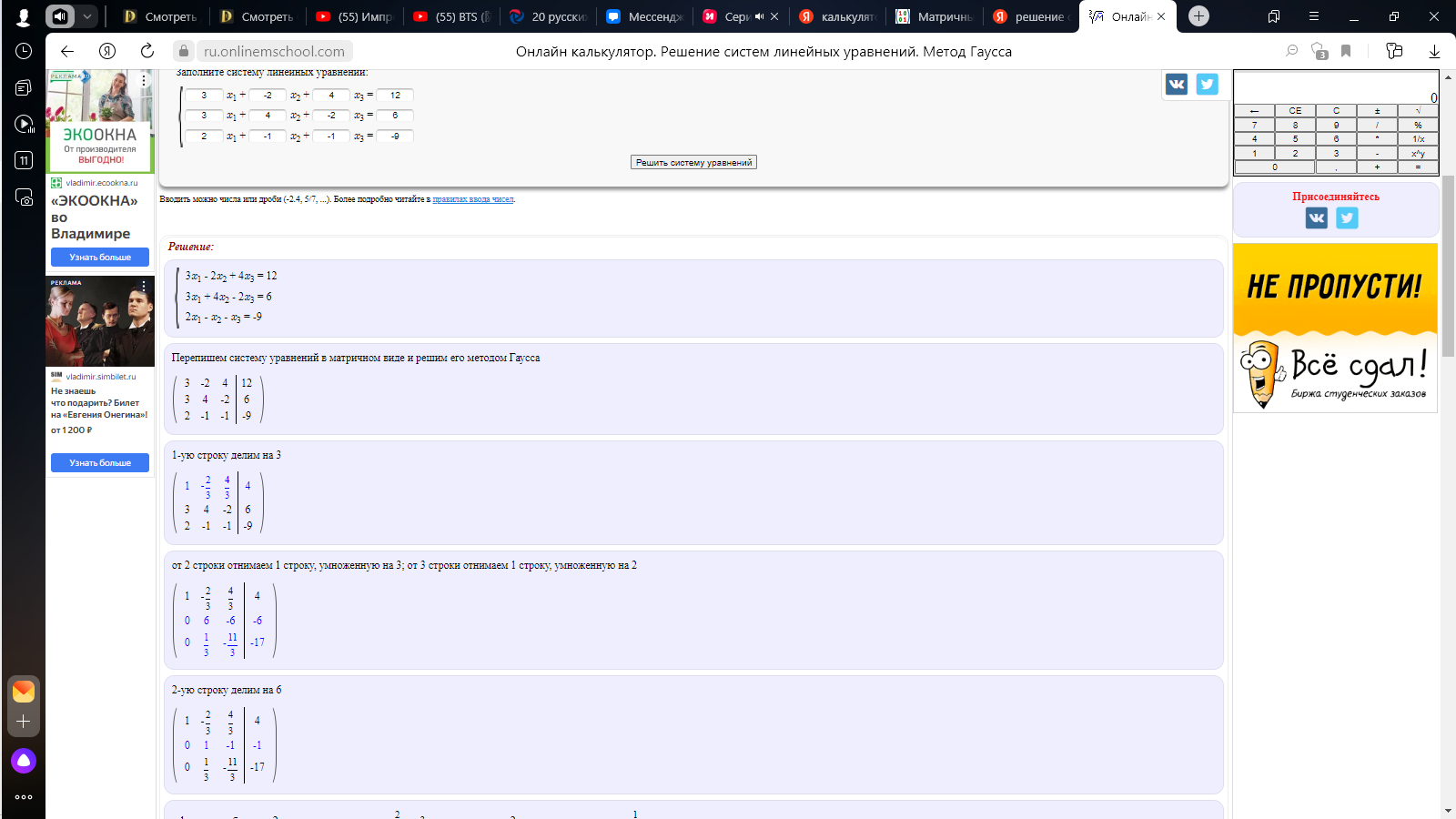
Ответы.Задание 1.

1. 
   -13 -3 5
   

6 -20 -14-5 -23 -2

2. 
   1)-2 48 12
   

5 -33 -7-1 27 72) 2 8 216 -2 -2023 -2 -28Они не являются перестановочными, так как А*В не равно В*А.

3. 
   Определитель А = 2.
   

4. 
   1/3 -1/6 0
   

-1/9 -5/18 1/31/3 4/3 -1Задание 2.

1. 
   Методом Крамера.
   

x=0, у=4, z=5.

2. 
   Матричным методом.
   

x=0, y=4, z=5.

3. 
   Методом Гаусса.
   

x=0, y=4, z=5.

---

Смотрите также файлы

• ПредисловиеВведениеО понятии проектного обучения.pdf

• Занятие для обучающихся по теме Счастлив тот, кто счастлив у себя дома.docx

• Нет, мне, быть может, не удалось стать очень хорошим. Это очень трудно. Но к этому, дети, я всегда стремился. Михаил Зощенко.pptx

• Пазухи носа и синуситы по локализации.docx

• Арбитражных судов в Российской Федерации.rtf