Файл: Графигі (0,в) жне ( ) нктелері арылы тетін тзу болатыны деттегідей тсіндіруге болады.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 24
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
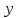
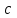
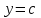
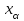
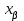
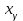
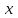
20.Сызықтық функция : у=ах+в, а
мен в нақты параметрлер, х
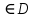=R=(-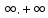
) анықталу облысы f(x) =ах+в – х айнымалысын а санына көбейтіп, оған в саның қосу ережесі f сәйкестігін анықтайды. Демек, у = f(x) 
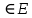екенін түсіндіру қиынға соқпайды. 
.y=ax+b E
t
D x.
Графигі (0,в) және (-
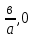) нүктелері арқылы өтетін түзу болатының әдеттегідей түсіндіруге болады. 30. Дәрежелік функция: у =а
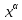, а
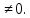D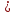
R, f ережесі х айнымалысын α дәрежесіне шығарып, а санына көбейту екенін көреміз, Е=R өзегеру облысы f заңдылығы функцияның характеристикасы, яғни сипаттаушы деп аталады. Бұл мысалға у =а 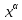өрнегімен беріліп отыр . 40. Көрсеткіштік функция у =
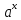,а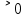
және а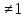
нақты параметр. D
R f заңдылығы х мәніне а санының х дәрежесін сәйкес қою ережесі: х→
, яғни х тің өзіне бейнесі сәйкес қойылып отыр. Егер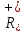 
= (0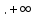
) оң нақты сандар жиыны болса, онда 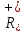=Е өзгеру облысы болып табылады. Функция характиристикасы f(x) = 50. Тригонометриялық екі функция: у= cos x, у= sin x, х
=R анықтамаларын оқушыға түсіндірейік. Жазықтықта UOV координаталар жүйесін алып, центрі бас нүкте болатын бірлік шеңберді аламыз. Шеңбердің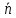 
=
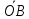вектор радиусын горизанталь OU осімен х бұрыш жасайтындай етіп, сағат тіліне қарсы бағытта бұрамыз. Сонда ∆АОВ тік бұрышты үшбұрыш пайда болады. Үшбұрыштың катеттерінің ұзындықтары сәйкес өзгеретінің оқушыға түсіндіреміз. Демек, ОА ұзындығын f(x) , ал АВ=ОС ұзындығын φ(x) деп белгілеуге ұғындырамыз. Демек, х шамасынан тәуелді екі функция анықталып отыр. Оның бірі φ(x) функциясы sin x деп аталса, екіншісі f(x) функциясы cos x деп белгіленген. АВ= φ(x) = sin x және ОА= f(x) = cos x. Сөйтіп, х→ АВ= sin x және х→ ОА= cos x екі сәйкестігін алдық. Синус сөзі латынша «иілу» ұғымын береді. Косинус сөзі толықтауыш бұрышын синусы деген түсінікті ұғындырады. Бұрыштың х шамасы әртүрлі бағытта бұру арқылы (-
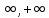) аралығында көреміз, ал тригонометриялық екі функция 
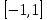аралығында өзгеретінің көреміз. Ендеше D=R жиыны, Е=
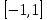жиыны болатындығы шығады. Сөйтіп, 1) Көрсеткіштік функцияға кері функция логарифмдік функцияға және 2) тригонометриялық функциялардың керілері кері тригонометриялық функцияларға тоқталмай-ақ, жиын ілімінің функция ұғымын енгізуде іргелік орны бар екеніне назар аударамыз.