Лабораторная работа №3

Разработка программ с использованием циклов.
Цикл — это последовательность операторов, повторяемая многократно. В С++ три
взаимозаменяемых оператора цикла — while, do while и for. При написании любого
цикла надо иметь в виду, что в нем всегда явно или неявно присутствуют четыре
элемента: начальные установки, тело цикла, модификация параметра цикла и выражение, проверяющее условие продолжения цикла (рис. 3.1). Начинающие чаще
всего забывают про первое и(или) третье.


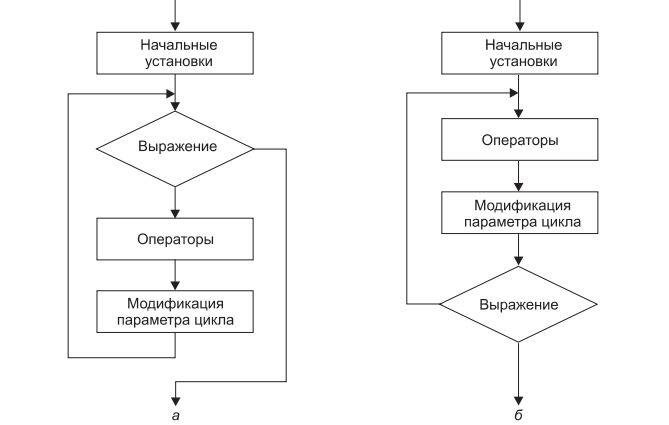
Рис. 3.1. Структурная схема операторов цикла: а — цикл с предусловием; 
б — цикл с постусловием
Операторы цикла

Операторы цикла задают многократное исполнение операторов тела цикла. Определены три разных оператора цикла:
Итерационный цикл for
Стандартный вид цикла for следующий:

for (инициализация_цикла; выражение-условие; список_выражений)

тело цикла
Оператор for имеет три главные части:

1. 
   инициализация_цикла – это место, где обычно находится оператор присваивания, используемый для установки начального значения переменной цикла.
   
2. 
   выражение-условие – это выражение, определяющее условие работы цикла.
   
3. 
   список_выражений – это место где определяется характер изменения переменной цикла на каждой итерации.
   

Цикл for работает до тех пор, пока условие истинно. Когда условие становится ложным, выполнение программы продолжается с оператора, следующего за циклом for.
Пример 1.

#include

using namespace std;

int main(void)

{

int x;

for(x=1; x<=100; x++) cout<endl;

return 0;

}
В цикле for проверка условия выполняется в самом начале. Это означает, что код в цикле может вообще не выполняться, если условие изначально ложно.
Цикл с предусловием while

while (выражение-условие)

тело цикла
Тело цикла – это или пустой, или простой, или составной оператор. Выражением-условием может быть любое выражение, имеющее в качестве истины ненулевое значение. Цикл выполняется, пока условие истинно. Когда условие становится ложным, выполняется строка, следующая за циклом.
Цикл с постусловием do/while
Цикл do/while проверяет условие в конце. То есть, цикл do/while всегда выполняется, хотя бы один раз. Стандартный вид цикла do/while следующий:
do{

последовательность операторов;

}while (выражение-условие);
Хотя в фигурных скобках нет необходимости при наличии одного оператора, они обычно используются для улучшения читабельности и устранения недоразумений (у читателя, а не у компилятора) по поводу цикла.
Во всех циклах тело цикла не может быть описанием или определением. Это либо отдельный оператор, который всегда завершается точкой с запятой, либо составной оператор, либо блок (заключается в фигурные скобки).
Оператор break
Оператор break имеет два назначения. Первое – это окончание работы оператора switch. Второе – это принудительное окончание цикла, минуя стандартную проверку условия.

Когда оператор break встречается в теле цикла, цикл завершается и выполнение программы переходит на строку, следующую за циклом.
Пример 2.
#include

using namespace std;

int main(void){

int x;

for(x=1; x<=100; x++) {

cout<
if(x==10) break;

}

return 0;

}

Данная программа выводит числа от 0 до 10 включительно и заканчивает работу, поскольку break вызывает немедленный выход из цикла, минуя условие x<100.
Оператор continue
Работа оператора continue чем-то похоже на работу оператора break. Но вместо форсированного окончания continue переходит к следующей итерации цикла, пропуская оставшийся код тела цикла. Например, следующая процедура выводит только положительные числа:

do{

cin>>x;

if(x<0) continue;

cout<< x <
} while(x!=100);

Метки и goto

Хотя goto уже давно не рекомендуют использовать, он по-прежнему используется в программах. goto требует наличия меток для работы. Метка – это корректный идентификатор С, завершаемый двоеточием. Метка должна находится в той же функции, что и goto.
Дальнейшие определения даются для целых чисел.

В случае, когда частное от деления a на b – целое, обозначая его буквой q, имеем a=bq, т.е. a представляется произведением b на целое. Мы говорим тогда, что a делится на b или b делит a. При этом aназываем кратным числа b.

Имеют место две следующие теоремы:

1. 
   Если a кратно m, m кратно b, то a кратно b.
   
2. 
   Если в равенстве вида k+l+…+n=p+q+…+s относительно всех членов, кроме какого-либо одного, известно, что они кратны b, то и этот один член кратен b.
   

Пример 3.

Разработаем программу, выводящую на консоль все целые неотрицательные решения уравнения x+2y=17.

Можно было бы перебирать все неотрицательные целые х от 0 до 17 и проверять, является ли целым числом или нет. Но, это потребует повторения цикла 18 раз. Поэтому будем перебирать все целые неотрицательные у от 0 до целой части , что потребует меньшего числа повторений цикла, и вычислять х по формуле . Если же ни одного решения не будет найдено выведем на консоль соответствующее сообщение.
#include

using namespace std;

int main()

{

registerint x, y;

bool flag = true;

for(y=0; y<=17/2; y++){

cout<<"x ="<<17-(2*y)<<" y ="<endl;

flag = false;

}

if(flag) cout<<"No roots"<
return 0;

}

Пример 4.

Написать программу печати таблицы значений функции



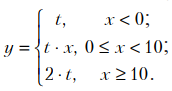
для аргумента, изменяющегося в заданных пределах с заданным шагом. Если t > 100,значения функции должны выводиться в целочисленном виде.Исходными данными являются начальное значение аргумента X_n, конечное значение аргумента X_k, шаг изменения аргумента dX и параметр t. Все величины — вещественные. Программа должна выводить таблицу, состоящую из двух столбцов: значений аргумента и соответствующих им значений функции.

В словесном виде алгоритм можно сформулировать так:

1. Ввести исходные данные.

2. Взять первое из значений аргумента.

3. Определить, какому интервалу из области определения функции принадлежит значение аргумента, и вычислить значение функции по соответствующей формуле.

4. Если t > 100, преобразовать значение y в целое.

5. Вывести строку таблицы.

6. Перейти к следующему значению аргумента.

7. Если оно не превышает конечное значение, повторить шаги 3–6, иначе закончить выполнение.

В каждый момент времени требуется хранить одно значение функции, поэтому для него достаточно завести одну переменную вещественного типа. Шаги 3–6 повторяются многократно, поэтому для их выполнения надо организовать цикл.

#include

#include

using namespace std;

int main() {

double Xn, Xk, dX, t, y;

cout<< "Enter Xn, Xk, dX, t" << endl;

cin>> Xn >> Xk >> dX >>t;

cout<< " --------------------------- " <<endl;

cout<< "| X | Y | " <<endl ;

cout<< " --------------------------- " << endl ;

for ( double x = Xn; x <= Xk; x += dX ) {

if ( x < 0 ) y = t;

if ( x >= 0 && x < 10 ) y = t * x;

if ( x >= 10 ) y = 2 * t;

if ( t > 100 ) cout<< x <<(int)y << endl;

else cout<< x<<" " <endl ;

}

cout<< " --------------------------- "<< endl;

return 0;

}

В программу введена вспомогательная переменная x, которая последовательнопринимает значения от Xn до Xk с шагом dX. Она определена непосредственно передиспользованием. Это является хорошим стилем, поскольку снижает вероятностьошибок (например, таких, как использование неинициализированной переменной).

Областью видимости переменной x является только цикл, что предпочтительнее, поскольку переменная x вне цикла не требуется.

Для преобразования в целое использована конструкция (int)y, унаследованная изязыка С.

Выполните программу несколько раз, задавая различные значения исходных данных. С помощью ручного подсчета убедитесь в правильности вычислений.
Пример 5.

Написать программу вычисления значения функции sin x (синус) с помощью бесконечного ряда Тейлора с точностью ε по формуле



Этот ряд сходится при |x| < ∞. Точность достигается при |R_n| < ε, где R_n —остаточный член ряда, который для данного ряда можно заменить величиной C_n очередного члена ряда, прибавляемого к сумме.

Общий алгоритм решения этой задачи достаточно прост: требуется задать начальное значение суммы ряда, а затем многократно вычислять очередной член ряда и добавлять его к ранее найденной сумме. Вычисления заканчиваются, когда абсолютная величина очередного члена ряда станет меньше заданной точности.

До выполнения программы предсказать, сколько членов ряда потребуется просуммировать, невозможно. В цикле такого рода есть опасность, что он никогда не завершится — как из-за возможных ошибок в вычислениях, так и из-за ограниченной области сходимости ряда (данный ряд сходится на всей числовой оси, но существуют ряды Тейлора, которые сходятся только для определенного интервала значений аргумента). Поэтому для надежности программы необходимо предусмотреть аварийный выход из цикла с печатью предупреждающего сообщения по достижении некоторого максимально допустимого количества итераций.

Прямое вычисление члена ряда по приведенной выше общей формуле, когда х возводится в степень, вычисляется факториал, а затем числитель делится на знаменатель, имеет два недостатка, которые делают этот способ непригодным. Первый недостаток — большая погрешность вычислений. При возведении в степень и вычислении факториала можно получить очень большие числа, при делении которых друг на друга произойдет потеря точности, поскольку количество значащих цифр, хранимых в ячейке памяти, ограничено. Кроме того, большие числа могут переполнить разрядную сетку. Второй недостаток — неэффективность вычислений: легко заметить, что в момент вычисления очередного члена ряда уже известен предыдущий, поэтому вычислять каждый член ряда «от печки» нерационально.

Для уменьшения количества выполняемых действий следует воспользоваться рекуррентной формулой получения последующего члена ряда через предыдущий

C_n+1 = C_n × T, где T — некоторый множитель. Подставив в эту формулу C_n и C_n+1, получим выражение для вычисления Т:


#include

#include

using namespace std;

int main() {

const int MaxIter = 500; // максимально допустимое количество итераций

double x, eps;

cout << "\nВведите аргумент и точность:\n";

cin >> x >> eps;

bool done = true; // признак достижения точности

double ch = x, y = ch; // первый член ряда и начальное значение суммы

for ( int n = 0; fabs( ch ) > eps; n++ ) {

ch *=- x * x / ( ( 2 * n + 2 ) *( 2 * n + 3 ) ); // очередной член ряда

y += ch; // добавление члена ряда к сумме

if ( n > MaxIter ) {

cout << endl<<"Ряд расходится!";

done = false; break; }

}

if ( done ) cout << "\nЗначение функции: " << y << " для х = " << x << endl;

}

Первый член ряда равен 1, поэтому, чтобы при первом проходе цикла значение второго члена вычислялось правильно, n должно быть равно 0. Максимально допустимое количество итераций удобно задать с помощью именованной константы.

Для аварийного выхода из цикла применяется оператор break (см. Учебник, с. 50),который выполняет выход на первый после цикла оператор.

Поскольку выход и в случае аварийного, и в случае нормального завершения циклапроисходит на один и тот же оператор, вводится булева переменная done, котораяпредотвращает печать значения функции, если точность вычислений не достигнута. Создание подобных переменных-«флагов», принимающих значение «истина»в случае успешного окончания вычислений и «ложь» в противном случае, являетсяраспространенным приемом программирования.Измените программу так, чтобы она печатала не только значения аргумента и функции, но и количество просуммированных членов ряда, и выполните программу несколько раз для различных значений аргумента и точности. Выявите зависимостьмежду этими величинами. В библиотеке есть функция cosh(x), вычисляющая гиперболический косинус. Ее прототип находится в файле <сmath>. Измените программу так, чтобы она рядом с вычисленным с помощью ряда значением печаталарезультат применения стандартной функции. Сравните результаты вычислений

Задание.

Согласно таблице 1 выбрать нужный вариант и разработать программу.
Задание 1. Разработать программу, которая выводит на консоль все целые неотрицательные решения уравнения

Задание 2. Вычислить и вывести на экран в виде таблицы значения функции, заданной с помощью ряда Тейлора, на интервале от x_нач до x_кон с шагом dx с точностью ε. Таблицу снабдить заголовком и шапкой. Каждая строка должна содержать значение аргумента, значение функции и количество просуммированных членов ряда.
Таблица 1

Номер варианта	Задание 1	Задание 2
1	4x+2y+z=52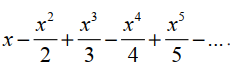
2	x2+y2=52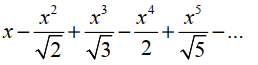
3	x3+2y2=52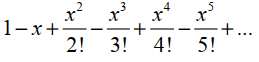
4	6x+3y+z=51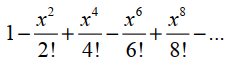
5	12x+36y+z=144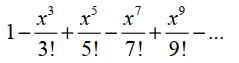

Контрольные вопросы:

1. 
   Приведите примеры реализации вечных циклов «for» и «while» на языке С++.
   

Требования к отчету

Отчет должен содержать:

1. 
   конспект теоретической части,
   
2. 
   лабораторное задание,
   
3. 
   блок-схему алгоритма,
   
4. 
   результаты выполнения программ.
   

#include

#include

using namespace std;

int main() {

double Xn, Xk, dX,x,eps;

cout << "Enter Xn, Xk, dX, eps" << endl;

cin >> Xn >> Xk >> dX >> eps;

cout << " --------------------------- " << endl;

cout << "| X | Y | " << endl;

cout << " --------------------------- " << endl;

const int MaxIter = 500; // максимально допустимое количество итераций

cout << "\nВведите аргумент и точность:\n";

cin >> x>>eps;

bool done = true; // признак достижения точности

double ch = x, y = ch; // первый член ряда и начальное значение суммы

for (int n = 0; fabs(ch) > eps; n++) {

ch *=pow(-x,n)/n // очередной член ряда

y += ch; // добавление члена ряда к сумме

if (n > MaxIter) {

cout << endl << "Ряд расходится!";

done = false; break;

}

}

if (done) cout << "\nЗначение функции: " << y << " для х = " << x << endl;

return 0;

}

---

Смотрите также файлы

• Протокол от 201 г. Председатель пцк утверждаю Зам директора по ур.docx

• Институт экономики и управления аэробика медицинская точка зрения.docx

• Исследовательский вопрос Кем был Золотой человек найденый в Иссыкском кургане.pptx

• Банкротства гражданина.docx

• Тесты по теме Учет основных средств Какой из нижеследующих бухгалтерских записей отражается хозяйственная операция по приобретению инвентаря стоимостью 6 000 000 руб за ед. (в т ч. Ндс) и сроком службы 6 месяцев.docx