ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 17
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.

| Область определения | Точек разрыва функции нет |
| Четность, периодичность | Функция общего вида |
| Поведение на концах области определения | |
| Асимптоты | y = (2·x+3)·e5·x Уравнения наклонных асимптот ищут в виде y = kx + b. По определению асимптоты: Находим коэффициент k: Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует. y = (2·x+3)·e5·x Найдем наклонную асимптоту при x → -∞: Находим коэффициент k: Находим коэффициент b: Получаем уравнение горизонтальной асимптоты: y = 0 |
| Промежутки монотонности | Первая производная. f'(x) = 5·(2·x+3)·e5·x+2·e5·x или f'(x)=(10·x+17)·e5·x Находим нули функции. Для этого приравниваем производную к нулю (10·x+17)·e5·x = 0 Откуда: x1 = -17/10 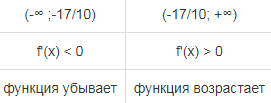 |
| Точки экстремума | В окрестности точки x = -17/10 производная функции меняет знак с (-) на (+). Следовательно, точка x = -17/10 - точка минимума. |
| Промежутки выпуклости | Вторая производная. f''(x) = 5·(10·x+17)·e5·x+10·e5·x или f''(x) = (50·x+95)·e5·x Находим корни уравнения. Для этого полученную функцию приравняем к нулю. (50·x+95)·e5·x = 0 Откуда точки перегиба: x1 = -19/10 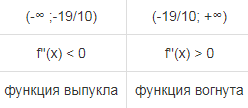 |
| Точки перегиба | x= -19/10 |
| Площадь криволинейной трапеции | |