Қ.Жұбанов атындағы Ақтөбе өңірлік университеті

ОСӨЖ

Тақырыбы: Кеплер заңдары.

Орындаған: Бердиклышева Г.

Тексерген: Таскалиев А.К.

2023ж

Кеплер заңдары.

Поляк ғалымы Николай Кперник (1473-1543ж.ж) өзінің Күн жүйесінің гелиоцентрлік моделін (үлгісін) жасаған кезде өте ертеде қалыптасқан планеталардың шеңбер бойымен тұрақты жылдамдықпен қозғалады деген қағидасын сақтап қалды.

Тек XVII ғасырдың басында ғана аспан денелерінің орбиталары шын мәнінде шеңберден өзгеше екені анықталды. Бұл маңызды жаңалықты неміс астрономы Иоганн Кеплер(1571-1630 жж) ашты. И.Кеплер планеталардың Н.Коперник іліміне сәйкес алдын ала есептелеген орындары мен бақылау кезіндегі анықталған орындарының бір-бірінен айырмашылығы бар екенін байқаған болатын. Демек планеталардың Күнді айнала қозғалу траекторялары шеңбер бойымен болады деген көзқарастан бас тарту қажет болды. Планеталардың гелиоцентрлік орбиталарының түрін (пішімін) анықтау үшін ол Дания астрономы Тихо Брагеннің(1546-1601 жж) өте мұқият жасаған Марс қозғалысына қатысты бақылау жұмыстарының нәтижелерін пайдаланды. Оның көп жылғы жұмысының нәтижесі – 1609-1619 жылдары планеталар қозғалысының үш негізгі заңын ашуы болды. Бұл заңдар оның есімімен Кеплер заңдары деп аталады.

I.Кеплердің бірінші заңы - планета орбитасының пішінін анықтайды: Барлық планеталар Күнді эллипс бойымен айналады, оның фокустарының бірінде Күн орналасады.



Эллипстің симметриялы центрі – О, үлкен АА1=2а және ВВ1=2в екі симметрия осі бар, мұндағы а – үлкен жарты ось, в – кіші жарты ось деп аталады.

Оның екі фокусы центрден OF1=OF2=c=a2-b2 қашықтықта орналасқан эллипстің негізгі қасиеті: эллипстің кез келген нүктесінің фокустардан қашықтықтарының қосындысы үлкен ось ұзындығына тең болатын тұрақты шама:

MF1+MF2=2a

e=c/a қатынасы эллипстің эксцентриситеті деп аталады. Ол эллипстің сопақтық дәрежесін көрсетеді: е неғұрлым үлкен болса, эллипстің шеңберден айырмашылығы да соғұрлым көп болады. Егер с=0 болса (эллипстің фокустары центрімен беттеседі), онда е=0, яғни эллипс радиусы а болатын шеңберге айналады. Шолпан мен Жер орбиталарының пішіндері шеңберге өте жақын (Шолпан орбитасының эксцентиситеті - 0,0068, Жердікі – 0,0167). Өзге планеталардың көпшілігінің орбиталары әлдеқайда созылыңқы болып келеді. Орбитаның Күнге ең жақын нүктесін перигелий (грекше peri-таяу, helios- Күн деген сөздерінен), оның ең алыс нүктесі афелий (грекше apo- алыс деген мағынаны білдіреді) деп аталады. Эллипстің үлкен а жарты осі планетаның Күннен орташа қашықтығына пара- пар. Астрономияда Жердің Күннен орташа қашықтығы Күн жүйесінде қолданылатын қашықтық өлшеу бірлігі ретінде қабылданған. Ол астрономиялық бірлік (а.б.) деп аталады: 1а.б.=149 600 000 км. Жердің табиғи серігі Айдың және кез келген жасанды серіктердің Жерге ең таяу келетін нүктесі перигей (грекше Гея- жер), ал ең алыс нүктесі апогей деп аталады.

---

Кеплердің күн жүйесі моделі


Оның екі фокусы центрден OF1=OF2=c=a2-b2 қашықтықта орналасқан эллипстің негізгі қасиеті: эллипстің кез келген нүктесінің фокустардан қашықтықтарының қосындысы үлкен ось ұзындығына тең болатын тұрақты шама:
MF1+MF2=2a
e=c/a қатынасы эллипстің эксцентриситеті деп аталады. Ол эллипстің сопақтық дәрежесін көрсетеді: е неғұрлым үлкен болса, эллипстің шеңберден айырмашылығы да соғұрлым көп болады. Егер с=0 болса (эллипстің фокустары центрімен беттеседі), онда е=0, яғни эллипс радиусы а болатын шеңберге айналады. Шолпан мен Жер орбиталарының пішіндері шеңберге өте жақын (Шолпан орбитасының эксцентиситеті - 0,0068, Жердікі – 0,0167). Өзге планеталардың көпшілігінің орбиталары әлдеқайда созылыңқы болып келеді. Орбитаның Күнге ең жақын нүктесін перигелий (грекше peri-таяу, helios- Күн деген сөздерінен), оның ең алыс нүктесі афелий (грекше apo- алыс деген мағынаны білдіреді) деп аталады. Эллипстің үлкен а жарты осі планетаның Күннен орташа қашықтығына пара- пар. Астрономияда Жердің Күннен орташа қашықтығы Күн жүйесінде қолданылатын қашықтық өлшеу бірлігі ретінде қабылданған. Ол астрономиялық бірлік (а.б.) деп аталады: 1а.б.=149 600 000 км. Жердің табиғи серігі Айдың және кез келген жасанды серіктердің Жерге ең таяу келетін нүктесі перигей (грекше Гей - жер), ал ең алыс нүктесі апогей деп аталады.

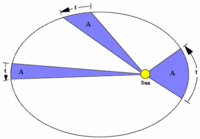
II. Кеплердің екінші заңы- аудандар заңы планета қозғалыстарының бірқалыпты емес екендігін анықтайды: планетаның радиус-векторы бірдей уақыт аралығында шамалары бірдей аудандар сызып шығады. Планеталар ең үлкен жылдамдықпен перигелийде, ал ең кіші жылдамдықпен афелий де қозғалады.



III. Кеплердің үшінші заңы- планеталардың орбиталық периодтары мен олардан Күнге дейінгі қашықтық арасындағы байланысты анықтайды: кез келген планетаның Күнді айналу периодтары жартыосьтерінің қатынасына тең болады. Екі планетаның үлкен жартыосіне а1 және а2 деп, ал айналу периодтары Т1 және Т2 деп белгілейтін болсақ, онда Кеплердің үшінші заңын мына түрде жазуға болады:



Ньютон өзінің бүкіләлемдік тартылыс заңын ашқан соң, Кеплердің үшінші заңын жалпы түрге келтіреді. Ол массалары М1 және М2 екі дене ауырлық центрін бір-бірінен а қашықтықта Т периодпен (мерзім ішінде) айналатын болса, мына

---

Қатынасы міндеті түрде орындалатынын дәләлдеді. Осы қатынастың көмегімен аспан денелерінің массаларын анықтау мүмкіндігі туды.

Пайдаланылған әдебиеттер:

1. 
    Қазақ энциклопедиясы
   
2. 
   ↑ Дубошин Г.Н., Небесная механика. Основные задачи и методы, 2 изд., М., 1968;
   
3. 
   ↑ Субботин М.Ф., Введение в теоретическую астрономию, М., 1968;Гребенников Е.А., Рябов Ю.А., Поиски и открытия планет, М., 1975.
   

---

Смотрите также файлы

• Теоретические аспекты психологической саморегуляции при хронических соматических заболеваниях 6.docx

• Реферат по дисциплине Почвоведение.docx

• Мчс россии.docx

• Учения Платона и Аристотеля о государстве.docx

• Секреты речи и текста Методика работы над текстом. Методика обучения сочинениюрассуждению.docx