Файл: Нестационарная теплопроводность с источником теплоты Рассматривается.docx
Добавлен: 05.12.2023
Просмотров: 65
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Нестационарная теплопроводность с источником теплотыРассматривается задача о динамике теплопроводности с источником теплоты в заданной области. Необходимо найти распределение температур в области, сравнить со стационарным распределением. 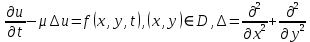Модель реализуется в программном пакете FreeFem++.Заданная область: Параметры области: W = 30кВт/м2 мощность источникаta = 25 C температура окруж средыmu = 16 m2/s температуропроводностьНестационарное уравнение теплопроводности, описывающее изменение температуры u(x,y,t) с течением времени, имеет вид:Для простоты рассматриваем случай, когда на границе области заданы граничные условия первого рода.Начальное распределение температуры удовлетворяет краевым условиям в начальный момент времени.Тогда вариационную формулировку для этой задачи можно записать в FreeFem++ как:// начальное распределениеfunc h = 25;// внешние источники мощности теплаfunc f = 30;// функции для граничных условийfunc g11 = 25; func g22 = 25; func g33 = 25; func g44 = 25; func g55 = 25; func g66 = 25;// слабая (вариационная) формулировкаproblem Heat(u,v) =int2d(Th)( u * v + mu*dt*(dx(u)*dx(v) + dy(u)*dy(v)) )- int2d(Th)( (uOld + dt * f) * v )+ on( g1, u = g11 ) + on( g2, u = g22)+ on( g3, u = g33 ) + on( g4, u = g44 ) + on( g5, u = g55 ) + on( g6, u = g66 )РезультатыРаспределение температуры в начальный момент времени t =0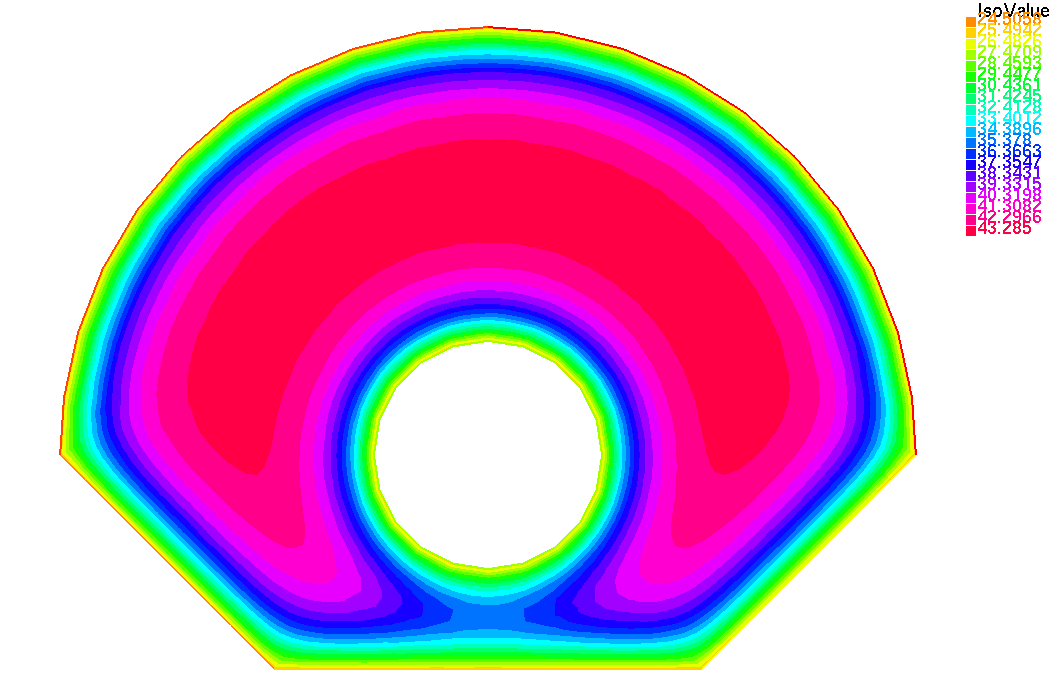Распределение температуры в момент времени t = 0.5 с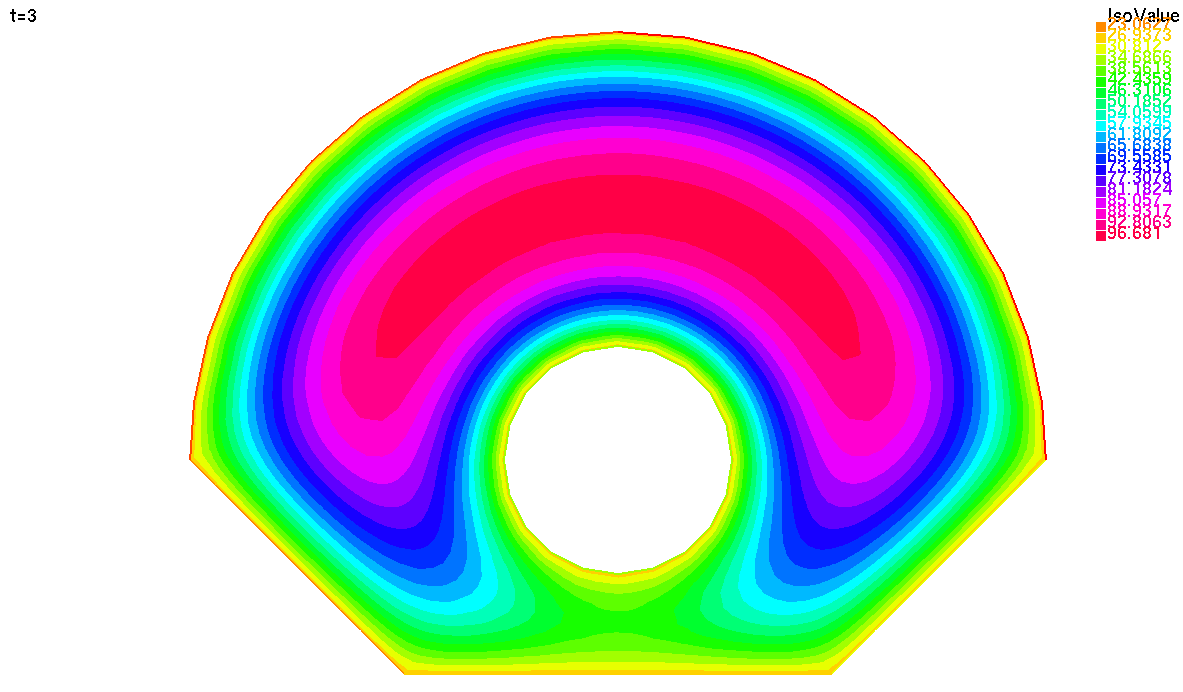Распределение температуры в момент времени t = 3 секунды
Распределение температуры в момент времени t = 12 секундРаспределение в момент времени t = 24 сек(вверху), стационарное распределение(внизу).Вывод: Таким образом, мы изучили методы численного решения задачи теплопроводности с источником теплоты и получили результаты в программном пакете FreeFem++. Как видно из изображений, стационарное распределение наблюдается на 24 секунде. Листинг – Программа «Нестационарное распределение теплопроводности»real t, dt;real mu = 16;int k = 0;border g1(t=0,pi/2){x=30*cos(t);y=30*sin(t);}//Граница g1border g2(t=pi/2,pi){x=30*cos(t);y=30*sin(t);} //Граница g2border g3(t=-30,-15){x=t;y=-t-30;} //Граница g3border g4(t=-15,15){x=t;y=-15;} //Граница g4border g5(t=15,30){x=t;y=t-30;} //Граница g5border g6(t=0,2*pi){x=8*cos(t);y=8*sin(t);} //Граница g6// ñòðîèì ñåòêó, íà êàæäîé ãðàíèöå ïî 5*n-óçëîâmesh Th = buildmesh(g1(10)+g2(10)+g3(10)+g4(10)+g5(10)+g6(-20));fespace Vh(Th, P2); // èñïîëüçóåì îáîçíà÷åíèÿ: u=u(x,y,(m+1)*dt), uOld=u(x,y,m*dt)Vh u, v, uOld;// îïðåäåëÿåì ôóíêöèþ -- íà÷àëüíîå ðàñïðåäåëåíèåfunc h = 25;// îïðåäåëÿåì ôóíêöèþ -- ïðàâóþ ÷àñòü óðàâíåíèÿfunc f = 30;// îïðåäåëÿåì ôóíêöèè äëÿ çàäàíèÿ ãðàíè÷íûõ óñëîâèéfunc g11 = 25; func g22 = 25;func g33 = 25; func g44 = 25;func g55 = 25; func g66 = 25;problem Heat(u,v) =int2d(Th)( u * v + mu*dt*(dx(u)*dx(v) + dy(u)*dy(v)) )- int2d(Th)( (uOld + dt * f) * v )+ on( g1, u = g11 ) + on( g2, u = g22)+ on( g3, u = g33 ) + on( g4, u = g44 ) + on( g5, u = g55 ) + on( g6, u = g66 ) ;t = 0; dt = 0.1;uOld = h;for (int m=0; m<240; m++){ t = t + dt;k = k+1;Heat; // âûçîâ ïðîöåäóðûuOld = u;if (k==10){ k = 0;plot(u,fill = 1,value =1);}plot(u, fill=1, value=1);}
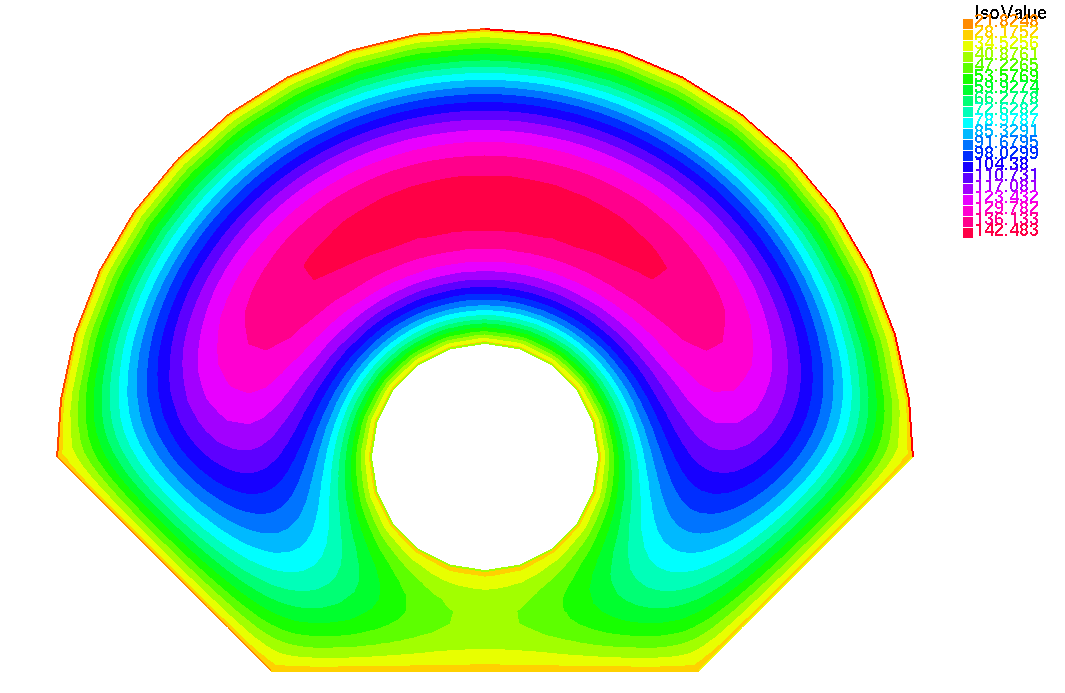
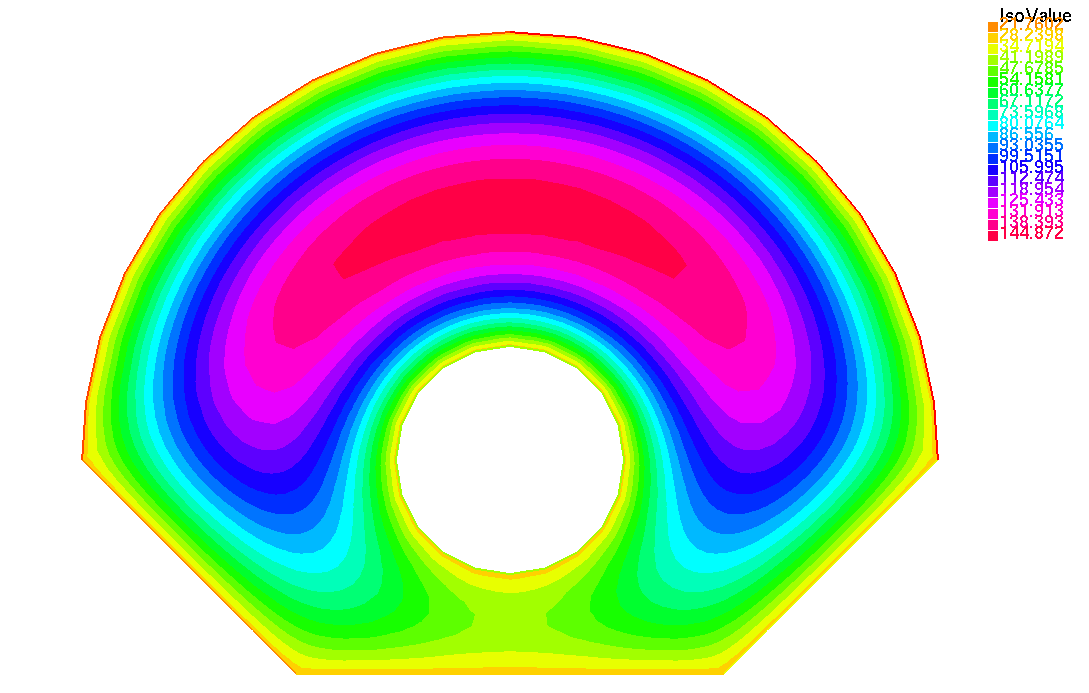
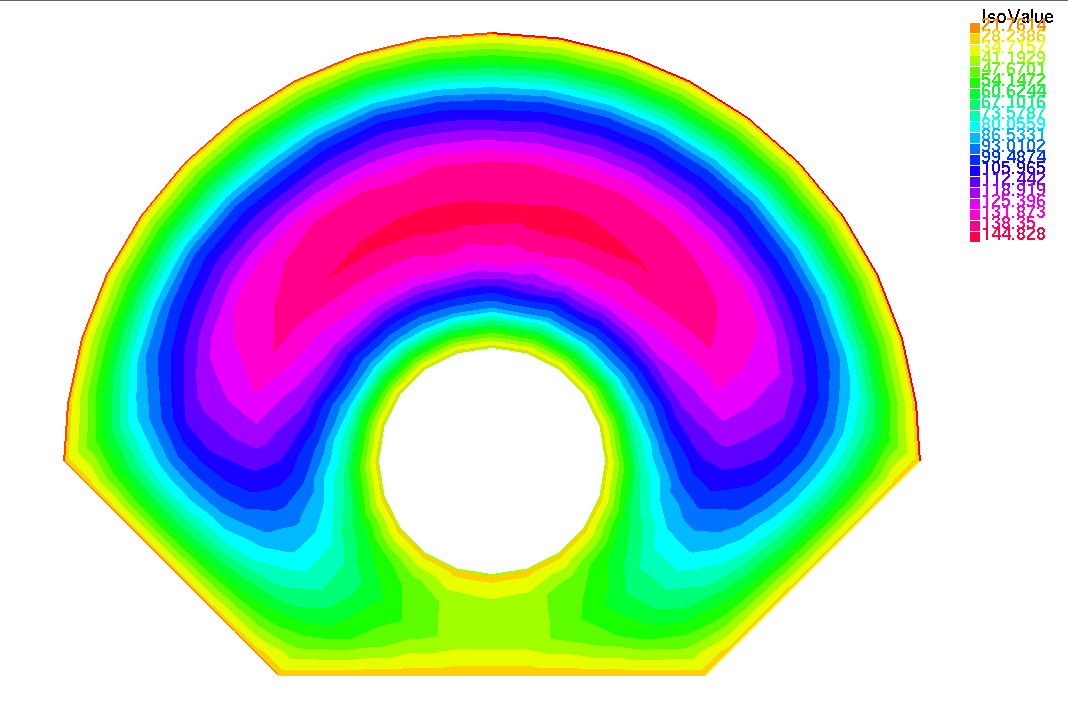
Распределение температуры в момент времени t = 12 секундРаспределение в момент времени t = 24 сек(вверху), стационарное распределение(внизу).Вывод: Таким образом, мы изучили методы численного решения задачи теплопроводности с источником теплоты и получили результаты в программном пакете FreeFem++. Как видно из изображений, стационарное распределение наблюдается на 24 секунде. Листинг – Программа «Нестационарное распределение теплопроводности»real t, dt;real mu = 16;int k = 0;border g1(t=0,pi/2){x=30*cos(t);y=30*sin(t);}//Граница g1border g2(t=pi/2,pi){x=30*cos(t);y=30*sin(t);} //Граница g2border g3(t=-30,-15){x=t;y=-t-30;} //Граница g3border g4(t=-15,15){x=t;y=-15;} //Граница g4border g5(t=15,30){x=t;y=t-30;} //Граница g5border g6(t=0,2*pi){x=8*cos(t);y=8*sin(t);} //Граница g6// ñòðîèì ñåòêó, íà êàæäîé ãðàíèöå ïî 5*n-óçëîâmesh Th = buildmesh(g1(10)+g2(10)+g3(10)+g4(10)+g5(10)+g6(-20));fespace Vh(Th, P2); // èñïîëüçóåì îáîçíà÷åíèÿ: u=u(x,y,(m+1)*dt), uOld=u(x,y,m*dt)Vh u, v, uOld;// îïðåäåëÿåì ôóíêöèþ -- íà÷àëüíîå ðàñïðåäåëåíèåfunc h = 25;// îïðåäåëÿåì ôóíêöèþ -- ïðàâóþ ÷àñòü óðàâíåíèÿfunc f = 30;// îïðåäåëÿåì ôóíêöèè äëÿ çàäàíèÿ ãðàíè÷íûõ óñëîâèéfunc g11 = 25; func g22 = 25;func g33 = 25; func g44 = 25;func g55 = 25; func g66 = 25;problem Heat(u,v) =int2d(Th)( u * v + mu*dt*(dx(u)*dx(v) + dy(u)*dy(v)) )- int2d(Th)( (uOld + dt * f) * v )+ on( g1, u = g11 ) + on( g2, u = g22)+ on( g3, u = g33 ) + on( g4, u = g44 ) + on( g5, u = g55 ) + on( g6, u = g66 ) ;t = 0; dt = 0.1;uOld = h;for (int m=0; m<240; m++){ t = t + dt;k = k+1;Heat; // âûçîâ ïðîöåäóðûuOld = u;if (k==10){ k = 0;plot(u,fill = 1,value =1);}plot(u, fill=1, value=1);}