П ЕРВОЕ ВЫСШЕЕ ТЕХНИЧЕСКОЕ УЧЕБНОЕ ЗАВЕДЕНИЕ РОССИИМИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИфедеральное государственное бюджетное образовательное учреждение высшего образованияСАНКТ-ПЕТЕРБУРГСКИЙ ГОРНЫЙ УНИВЕРСИТЕТ Кафедра общей и технической физикиОтчет по лабораторной работе №1По дисциплине: ФизикаПо теме: Измерение длины световой волны с помощью бипризмы ФренеляВыполнил: студент гр. ТО-21 Леус А.Ю.

(Подпись)

(Ф.И.О.)

Проверил:

(Подпись)

(Ф.И.О.)

Санкт-Петербург2023Цель работы: определение длины световой волны с помощью бипризмы Френеля, создающей два мнимых когерентных источника излучения.Краткое теоретическое содержаниеЯвление, изучаемое в работе: интерференция света.Основные определения физических величин, явлений, процессовИнтерференция света - сложение световых пучков, ведущее к образованию светлых и темных полос, которые можно наблюдать визуально.Волна – это распространение колебательного пространства со временем.Фаза волны – аргумент периодической функции, описывающей колебательный процесс.Длина волны – расстояние между ближайшими частицами, колеблющимися в одинаковой фазе.Когерентные волны

---

– волны, характеризующиеся одинаковой частотой и постоянством разности фаз в заданной точке.

Оптическая разность хода – разность длин путей, которые пройдут лучи света от источников до точки, в которой наблюдается интерференция.

Интенсивность волны – скалярная величина, равная модулю среднего значения вектора Умова.
Законы и соотношения, лежащие в основе лабораторной работы
Условия явления интерференции. Так как наша лабораторная работа строится на явлении интерференции, то нужно упомянуть о том, что наблюдать интерференционную картину можно лишь в том случае, если интерферирующие волны имеют одинаковую частоту и постоянную разность фаз.

Источники света и испускаемые ими лучи, удовлетворяющие указанным требованиям, называются когерентными. Только когерентные источники света дают стабильную во времени интерференционную картину.

Принцип Гюйгенса-Френеля. Каждая точка среды, до которой дошло возмущение, сама становится источником вторичных когерентных волн.

Принцип суперпозиции. В среде могут распространяться колебания, исходящие от разных центров. Если две различные системы волн, исходящие из разных источников, перекрываются в некоторой области, а затем снова рас­ходятся, то дальше каждая из них распространяется так, как если бы она не встречала на своем пути другую. Этот принцип независимо­сти распространения волн называется принципом суперпозиции.

Пусть до какой-либо точки сферы доходят две волны. Тогда при наложении двух волновых процессов каждая точка среды становится источником двух колебаний. В случае, если амплитуды слагаемых ко­лебаний одинаковы, результат сложения двух колебаний может быть выражен так:



Полученное выражение представляет собой гармоническое колеба­тельное движение, которое может быть записано следующим образом:

---

,

где  - начальная фаза результирующих колебаний,

- амплитуда результирующих колебаний.

Поскольку энергия колебательного движения пропорциональна квадрату амплитуды, то энергия результирующих колебаний  W' будет связана с энергией слагаемых колебаний W следующим соотношением:



Это соотношение показывает, что если



где n - целое число, то и W '= 4W, т.е. энергия результирующих колебаний в местах, где фазы колебаний совпадают, равна не сумме энергий составляющих колебаний, а в два раза больше этой суммы. Этот результат означает, что при интерференции происходит перераспределение энергии волн в пространстве.

Экспериментальная установка:

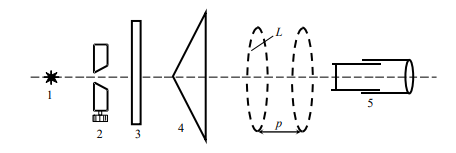
Пояснение к схеме:

1 - источник света;

2 – щель;

3 – светофильтр;

4 - бипризма Френеля;

5 - измерительный микроскоп;

L – линза.

Основные расчётные формулы


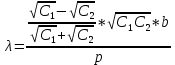
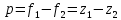
λ – длина волны (мм);

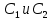- расстояния между изображениями щелей (мм);

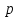- величина смещения линзы из положения 1 в положение 2 (мм);

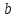- расстояние между серединами соседних интерференционных полос (мм);

---

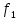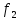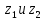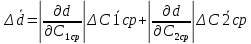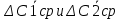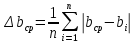
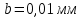
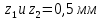
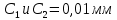
- расстояние от места расположения мнимых источников до линзы (мм); – расстояние между линзой и фокальной плоскостью микроскопа (мм); - положения линзы, при которых в окуляр микроскопа будут отчетливо видны изображения двух мнимых источников света в виде двух ярких полосок (мм).Формулы косвенных погрешностей , где – средние абсолютные величиныПогрешности прямых измеренийТаблицы

№ измерения	Отсчет слева, мм	Отсчет справа, мм	Разность отсчетов, мм	Число полос	, мм
1	23,58	27,60	4,02	5	0,80
2	23,56	27,46	3,90	5	0,78
3	23,53	27,54	4,01	5	0,80
4	23,69	27,61	3,92	5	0,78
5	23,57	27,59	4,02	5	0,80

Таблица 1

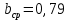
№ п/п	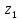, мм	Отсчет поля мнимых ист-в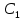, мм		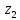, мм		, мм		Отсчет пол-я из-й мнимых ист-в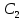, мм			, мм		, мм
		левого	правого					левого		правого
1	275	16,06	16,46	0,40		435		17,40		17,54	0,14		160
2		16,11	16,59	0,48		435		17,38		17,60	0,22		160
3		16,08	16,41	0,33		435		17,46		17,58	0,12		160
4		16,13	16,62	0,49		435		17,36		17,49	0,13		160
5		16,09	16,53	0,44		435		17,43		17,57	0,14		160
Среднее		16,09	16,52		0,43	435	17,40		17,56		0,16	160

---

Таблица 2Пример вычислений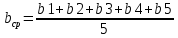= = 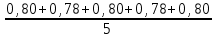0,79 мм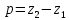= 435 – 275 = 160 мм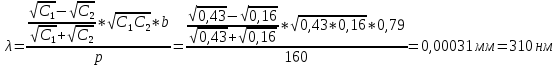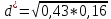= 0,26 ммa = 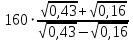= 660,5 ммПогрешности косвенных измерений:1) Рассчитаем погрешность измерений ширины интерференционной полосы b: = = 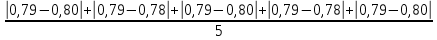0,01 мм -средняя абсолютная ошибка . 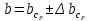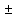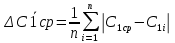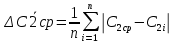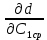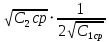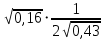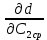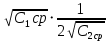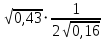Таким образом: = 0,79 0,01 мм2)Рассчитаем погрешность измерений расстояния между мнимыми источниками d: , где – средние абсолютные величины = 0,05 мм = 0,03 мм = = = 0,3 = = = 0,8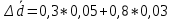 = 0,04 мм. Таким образом: 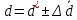= 0,26 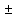0,04 мм3)Рассчитаем погрешность измерений расстояния от мнимых источников до фокальной плоскости микроскопа а: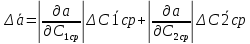+ 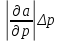= 21,9 ммТаким образом:

---

Смотрите также файлы

• Реферат Нанохимия путь к высоким технологиям xxi века.rtf

• Наддолотные управляемые системы NeoSteer студент гр. Днннб 411.pptx

• 1. Изучение Устава предприятия.docx

• Ргр Динамика вращательного движения Условие задачи.docx

• Тема день конституции.pdf