Добавлен: 05.12.2023
Просмотров: 83
Скачиваний: 14
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра ЭУТ
Курсовая РАБОТА
по дисциплине «Методы анализа и обработки сигнала»
Тема: Обработка случайных сигналов
| Студентка гр. 0587 | | Гребнева Ю.Д. |
| Преподаватель | | Вагин А.В. |
Санкт-Петербург
2023
ЗАДАНИЕ
на курсовую работу
| Студентка Гребнева Ю.Д. |
| Группа 0587 |
| Тема работы: Обработка случайных сигналов |
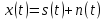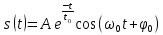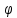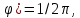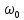| Исходные данные: Вариант №1 На вход приемного тракта дефектоскопа поступает сигнал:  где s(t) – случайный сигнал, n(t) – квазибелый гауссовский шум.  где A – случайная амплитуда, распределенная по закону Рэлея,  – случайная начальная фаза, распределенная по закону P(  – круговая частота.Спектральная плотность гауссовского белого шума: 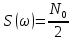 При этом     |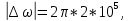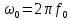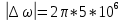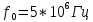
Требуется определить:
1. Максимально допустимое значение параметра
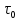, если ультразвуковой дефектоскоп должен раздельно принимать сигналы от дефектов, отстоящих по глубине на 3 мм по стали. За меру разрешающей способности принимается значение аргумента
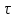нормированной функции неопределенности при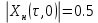 
2. Структуру согласованного фильтра и параметры (ширина полосы пропускания и изменение отношения сигнал/помеха на выходе по сравнению со входом) квазиоптимального фильтра, состоящего из 1 колебательного контура.
3. Зависимость
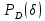, где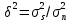 
на входе приемного тракта, если обнаружитель выполнен по схеме согласованный фильтр – линейный детектор – пороговое устройство. Результаты сравнить с работой простейшего обнаружителя Неймана -Пирсона. При этом с доверительной вероятностью 
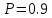должно быть не более 
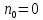ложного срабатывания регистратора дефектов в 
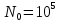независимых точках контроля.Содержание пояснительной записки:
«Содержание», «Введение», «Заключение», «Список использованных источников»)
| Предполагаемый объем пояснительной записки: Не менее 20 страниц. | ||
| Дата выдачи задания: 20.03.2023 | ||
| Дата сдачи реферата: 27.04.2023 | ||
| Дата защиты реферата: 13.05.2023 | ||
| Студентка | | Гребнева Ю.Д. |
| Преподаватель | | Вагин А.В. |
Аннотация
Ультразвуковой дефектоскоп применяется в различных областях, где необходимо обнаруживать дефекты в материалах и конструкциях. Например, он используется в металлургии для контроля качества сварных соединений, в авиации для обнаружения трещин и других дефектов в летательных аппаратах, в медицине для диагностики заболеваний и т.д.
В данной курсовой работе было произведено: нахождение параметра, определяющего длительность радиоимпульса с заданной формой огибающей
по заданной разрешающей способности, определение параметров квазиоптимального фильтра, максимизирующего отношение сигнал/помеха для заданного сигнала, получена зависимость вероятности правильного обнаружения от отношения сигнал/помеха на выходе по сравнению с входом.
SUMMARY
Ultrasonic flaw detector is used in various fields where it is necessary to detect defects in materials and structures. For example, it is used in metallurgy to control the quality of welded joints, in aviation to detect cracks and other defects in aircraft, in medicine to diagnose diseases, etc.
In this course work, the following was performed: finding a parameter that determines the duration of a radio pulse with a given envelope shape
according to a given resolution, determining the parameters of a quasi-optimal filter that maximizes the signal/interference ratio for a given signal, the dependence of the probability of correct detection on the signal/interference ratio at the output compared to the input was obtained.
содержание
| | Введение | 5 |
| 1. | Определение параметра  | 6 |
| 2. | Определение структуры согласованного и параметров квазиоптимального фильтра, состоящего из 1 колебательного контура | 8 |
| 2.1. | Построение согласованного фильтра | 8 |
| 2.2. | Построение квазиоптимального фильтра | 10 |
| 3. | Определение характеристик обнаружителя сигнала | 13 |
| | Заключение | 15 |
| | Список использованных источников | 16 |
| | Приложение А. Расчёты в MatLab | 17 |
введение
Для выполнения курсовой работы по дисциплине "Методы анализа и обработки сигналов" необходимо применить навыки, полученные при изучении данной дисциплины и предшествующих дисциплин («Основы теории сигналов»). В процессе выполнения курсовой работы и зависимости от полученного задания студенты должны научиться оценивать статистические характеристики случайных процессов по выборочным значениям, приобрести практические навыки расчета характеристик обнаружения сигналов или определения точности измерения параметров, изучить методы построения и расчета параметров оптимальных и квазиоптимальных фильтров, максимизирующих отношение сигнал/помеха, и приобрести навыки определения параметров сигнала на выходе фильтра, освоить способы определения разрешающей способности сигналов и систем, их использующих.
1. ОПРЕДЕЛЕНИЕ ПАРАМЕТРА
. Полезный сигнал, поступающий на вход приемного тракта дефектоскопа
Функция неопределенности задается следующим выражением (1), воспользуемся ей для определения
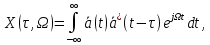:| |  | (1) |
где
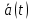– комплексная огибающая сигнала.По условию случайная фаза сигнала равномерно распределена в интервале
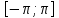. В связи с этим для вычисления функции неопределенности подставим в формулу выражение для сигнала, в котором за 
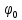примем среднее значение фазы равное нулю. 
=
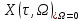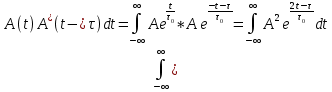
За меру разрешающей способности принимается значение
аргумента нормированной функции неопределенности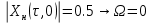 
.Преобразуем подынтегральное выражение
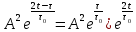
Тогда учитывая, что
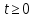
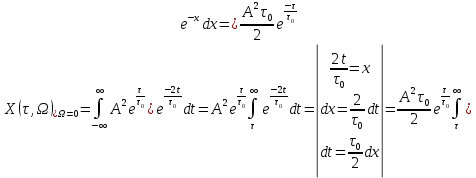
Следовательно, выражение для функции неопределенности примет вид
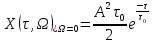
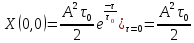
Нормированная функция неопределенности:
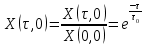
Найдём численное значение параметра
:
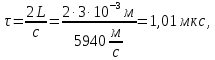
где
с – скорость распространения звука в рассматриваемой среде (стали)- 5940м/с, L- расстояния между объектами
Подставим это значение в выражение для нормированной функции неопределенности и найдем параметр
:
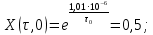
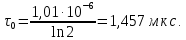
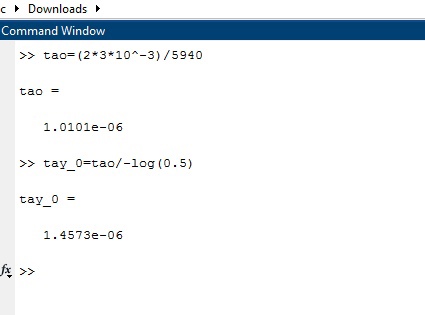
Рисунок 1- Определение длительности сигнала
2. определение структуры согласованного и параметров квазиоптимального фильтра, состоящего из 1 колебательного контура
2.1. Построение согласованного фильтра
Комплексная частотная характеристика оптимального фильтра в случае помехи с постоянной спектральной плотностью в диапазоне частот, покрывающем весь спектр сигнала, задается следующей формулой (14):
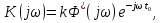| |  | (14) |
где
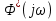- комплексно-сопряженное значение амплитудного спектра сигнала, k- постоянная.
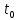– момент времени, соответствующий окончанию интервала, содержащего основную долю энергии сигнала.Проверим второе условие физической реализуемости:
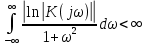
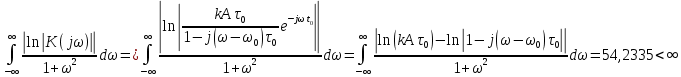
Исходя из того, что интеграл равен числу (Приложение А) первое условие физической реализуемости выполняется.
Рассчитаем комплексно-амплитудный спектр сигнала:
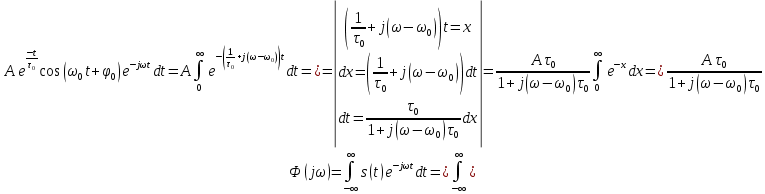
Таким образом, спектр сигнала
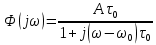
Частотная характеристика согласованного фильтра будет определяться следующим выражением
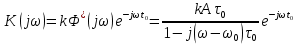
Здесь ????0 выбирается в момент времени, соответствующий окончанию интервала, содержащего основную долю энергии сигнала (0.9????