Добавлен: 05.12.2023
Просмотров: 84
Скачиваний: 14
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
????):
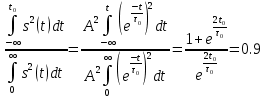
Таким образом,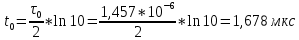
Проверим второе условие реализуемости данного фильтра с помощью импульсной характеристики согласованного фильтра
, если фильтр реализуем, то 
:
ИПФ согласованного фильтра определяется следующим выражением:
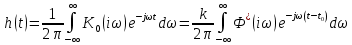
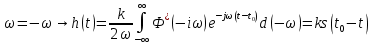
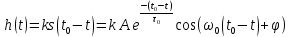
Результат расчета представлен на рисунке 2- условие не соблюдается
, значит, построение согласованного фильтра невозможно. 
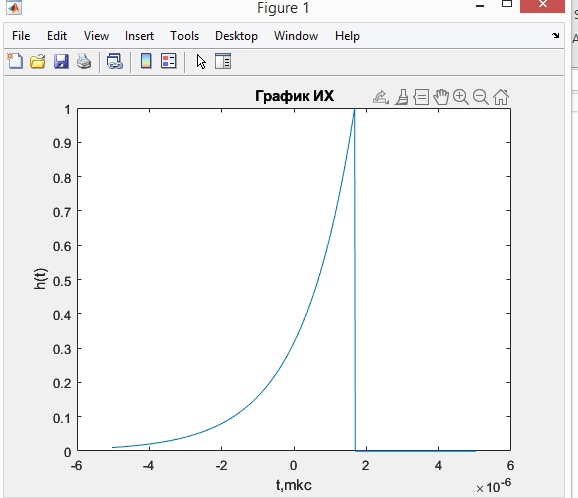
Рисунок 2- Проверка фильтра на физическую реализуемость
2.2 Построение квазиоптимального фильтра
Рассчитаем заданный квазиоптимальный фильтр. Его отношение сигнал/помеха на выходе лишь немного меньше значения, рассчитываемого для согласованного фильтра. Тогда ухудшение отношения сигнал/помеха на выходе квазиоптимального фильтра по сравнению с этим отношением на выходе оптимального фильтра равно:
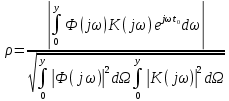
По условию квазиоптимальный фильтр состоит из 1 колебательного контура. Тогда его частотная характеристика равна:
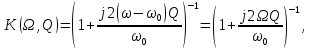
Где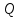
– добротность фильтра,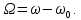 
Верхний предел интегрирования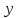
найдем следующим образом (Приложение А). То есть верхний предел интегрирования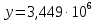 
Преобразуем выражение для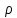
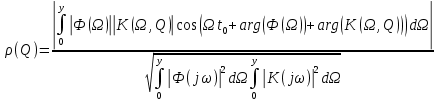
Подставим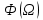
и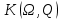 
в выражение для 
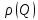и вычислим 
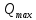, при котором достигается максимальное отношение сигнал/помеха. На рисунке 2 показана зависимость ухудшения отношения сигнал/помеха на выходе квазиоптимального фильтра от добротности конутра. Вычисления представлены ниже (Приложение А).
Используя вычислительный пакет Matlab получаю максимальное отношение сигнал/помеха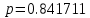
, оптимальная добротность 
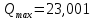, проигрыш составляет 15,828%.
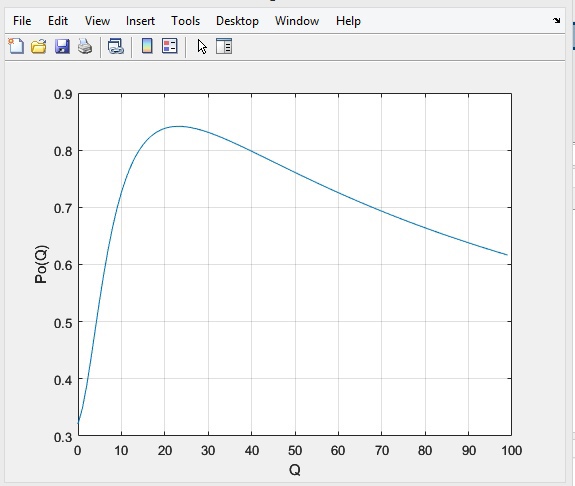
Рисунок 3- Ухудшение отношения сигнал/помеха на выходе
Полуширина частотной характеристики одиночного контура:
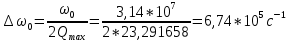
Ширина частотной характеристики одиночного контура:
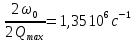
Отношение сигнал/помеха на выходе квазиоптимального фильтра выражается через отношение сигнал/помеха на входе:
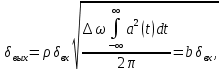
где
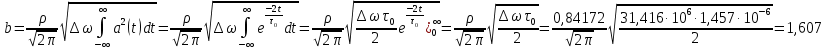
Ниже представлены вычисления (Приложение А). В итоге b=1,607
3. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ОБНАРУЖИТЕЛЯ СИГНАЛА
Обнаружитель Неймана-Пирсона соответствует обнаружению очень короткого сигнала. При обнаружении сигналов конечной длительности, если не требуется очень высокое быстродействие, целесообразно строить обнаружитель так, чтобы использовать полную энергию сигнала. Под простейшим обнаружителем Неймана Пирсона принимается схема линейный детектор – пороговое устройство.
В нашей работе используется оптимальный обнаружитель, который помимо порогового устройства включает в себя оптимальный фильтр, который ослабляет помехи. Обнаружитель состоит из следующих блоков: согласованный фильтр (1), линейный детектор (2), пороговое устройство (3).
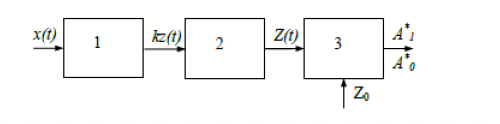
Рисунок 4 – Структура оптимального обнаружителя
Формула вероятности правильного обнаружения простейшего обнаружителя Неймана Пирсона:
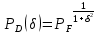
В оптимальном обнаружителе используется фильтр:
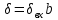
Вероятность правильного обнаружения сигнала оптимального обнаружителя равна:
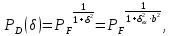
где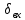
- отношение сигнал/помеха на входе фильтра.
Вероятность перебраковки
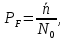
где в числителе стоит среднее количество ложных регистраций определяется из трансцендентного уравнения:
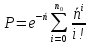
Так как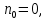
то
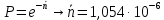
Рассчитаем вероятность ложной тревоги, зная по исходным данным N0 = 106:
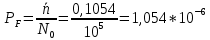
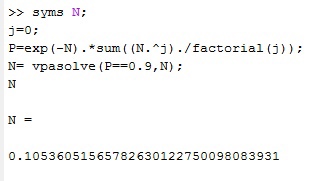
Рисунок 5- Нахождение среднего количества ложных регистраций
На рисунке 6 изображены характеристики обнаружения для оптимального обнаружителя и для обнаружителя Неймана-Пирсона.
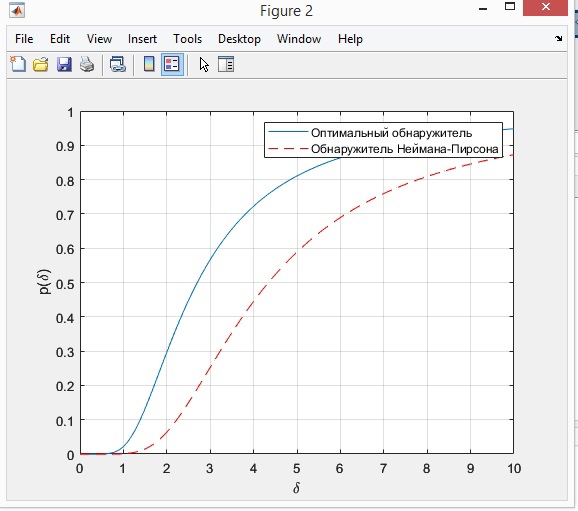
Рисунок 6- Зависимость вероятности правильного обнаружения от отношения сигнал/помеха на входе приемного тракта
ЗАКЛЮЧЕНИЕ
Максимально допустимое значение параметра
, если ультразвуковой
дефектоскоп должен раздельно принимать сигналы от дефектов, отстоящих по глубине на 3 мм по стали, составляет 1,457 мкс.
Исходя из того, что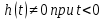
, можно сделать вывод, что построение согласованного фильтра невозможно. Нами был построен квазиоптимальный фильтр, состоящий из 1 колебательного контура, близкий по отношению сигнал/помеха к согласованному. Ширина полосы пропускания фильтра составляет 0,216 МГц. Оптимальное значение добротности составляет 23,001, а значение коэффициента b= 1,607.
Определили зависимость
на выходе приёмного тракта, при этом
среднее количество ложных регистраций 0,1054, вероятность перебраковки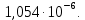
СПИСОК ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ
системах интроскопии: Учеб.пособие / ЛЭТИ. Л., 1990.
Приложение А
l = 3*10^-3;
c = 5940;
tao = (2.*l)/c;
% Определение длительности сигнала
tao_0 = tao/-log(0.5);
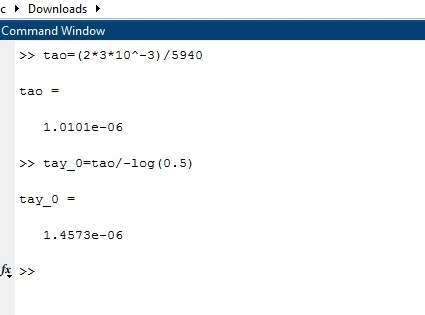
% Построение графика импульсной характеристики
Sp = @(t) (exp(-t./tao_0) .* heaviside(t))
» t_0=1.678e-06;
» tao_0=1.4573e-06;
» t = -3 * t_0 : t_0 / 100 : 3 * t_0;
» plot(t, Sp(t_0-t))
» title('График ИХ')
» xlabel('t,mkc')
» ylabel('h(t)')
f0 = 5e6;
w0 = 2*pi*f0;
deltaw = 2*pi*5e6;
n = 1; %число несвязанных колебательных контуров
P = 0.9; %Доверительная вероятность
n0 = 0; %Число ложных срабатываний
N0 = 1e5;%число импульсов
l = 3e-3;%разрешающая способность
tau0 =1.4573e-06;
t0 = (tau0/2)*log(10);
syms w
J = tau0/(1-1i*(w-w0)*tau0)*exp(-1i*w*t0);
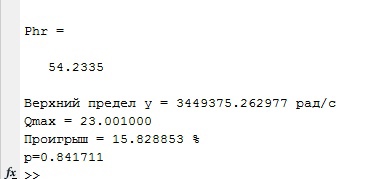
Phr = double(vpaintegral(abs(log(abs(J)))/(1+w^2),w,[-inf inf])) %Проверка условия физической реализуемости фильтра
tau0 =1.4573e-06;
t0 = (tau0/2)*log(10);
syms y omega
F = tau0/(1+1i*omega*tau0);
X = int(abs(F)^2,omega,[0 y])/int(abs(F)^2,omega,[0 deltaw/2]);
y = solve(X-0.9,y);
fprintf('Верхний предел y = %f рад/c\n', y);
syms Q Po Fi
K = 1/sqrt(1+(2*omega*Q/w0)^2)^n;
Fi = -n*atan(2*omega*Q/w0);
Po = abs(vpaintegral(abs(F)*K*cos(omega*t0+angle(F)+Fi),omega,[0 y]))/sqrt(vpaintegral(abs(F)^2, omega, [0 y])*vpaintegral(K^2, omega, [0 y]));
q = 0.001:1:100;
r =(subs(Po, {Q}, {q}));
plot(q, r);
grid on;
xlabel('Q');
ylabel('Po(Q)');
hold off;
[m_ro, idx] = max(r);
Qmax = q(idx);
fprintf('Qmax = %f \nПроигрыш = %f %% \n', Qmax, (1-m_ro)*100);
fprintf('p=%f\n', p);
b = 1.607;
Pf = 0.1054/N0;
delta = 0:0.1:10;
P = Pf.^(1./(1+b^2*delta.^2));
Ph = Pf.^(1./(1+delta.^2));
figure
plot(delta, P);
grid on;
xlabel('\delta');
ylabel('p(\delta)');
hold on;
plot(delta, Ph, 'r--')
legend('Оптимальный обнаружитель', 'Обнаружитель Неймана-Пирсона');
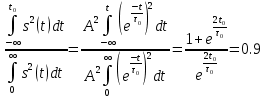
Таким образом,
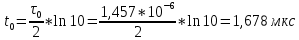
Проверим второе условие реализуемости данного фильтра с помощью импульсной характеристики согласованного фильтра
, если фильтр реализуем, то :ИПФ согласованного фильтра определяется следующим выражением:
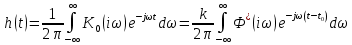
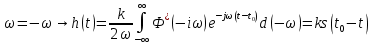
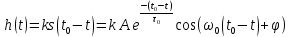
Результат расчета представлен на рисунке 2- условие не соблюдается
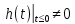, значит, построение согласованного фильтра невозможно. Рисунок 2- Проверка фильтра на физическую реализуемость
2.2 Построение квазиоптимального фильтра
Рассчитаем заданный квазиоптимальный фильтр. Его отношение сигнал/помеха на выходе лишь немного меньше значения, рассчитываемого для согласованного фильтра. Тогда ухудшение отношения сигнал/помеха на выходе квазиоптимального фильтра по сравнению с этим отношением на выходе оптимального фильтра равно:
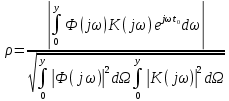
По условию квазиоптимальный фильтр состоит из 1 колебательного контура. Тогда его частотная характеристика равна:
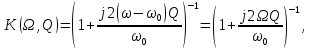
Где
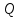– добротность фильтра,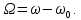 Верхний предел интегрирования
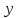найдем следующим образом (Приложение А). То есть верхний предел интегрирования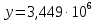 Преобразуем выражение для
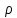
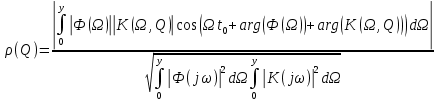
Подставим
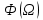и 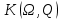в выражение для 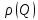и вычислим 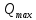, при котором достигается максимальное отношение сигнал/помеха. На рисунке 2 показана зависимость ухудшения отношения сигнал/помеха на выходе квазиоптимального фильтра от добротности конутра. Вычисления представлены ниже (Приложение А).Используя вычислительный пакет Matlab получаю максимальное отношение сигнал/помеха
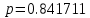, оптимальная добротность 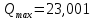, проигрыш составляет 15,828%. Рисунок 3- Ухудшение отношения сигнал/помеха на выходе
Полуширина частотной характеристики одиночного контура:
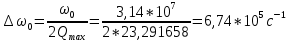
Ширина частотной характеристики одиночного контура:
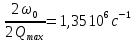
Отношение сигнал/помеха на выходе квазиоптимального фильтра выражается через отношение сигнал/помеха на входе:
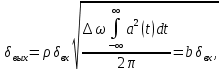
где
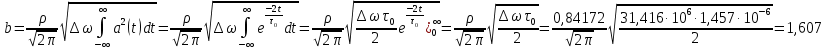
Ниже представлены вычисления (Приложение А). В итоге b=1,607
3. ОПРЕДЕЛЕНИЕ ХАРАКТЕРИСТИК ОБНАРУЖИТЕЛЯ СИГНАЛА
Обнаружитель Неймана-Пирсона соответствует обнаружению очень короткого сигнала. При обнаружении сигналов конечной длительности, если не требуется очень высокое быстродействие, целесообразно строить обнаружитель так, чтобы использовать полную энергию сигнала. Под простейшим обнаружителем Неймана Пирсона принимается схема линейный детектор – пороговое устройство.
В нашей работе используется оптимальный обнаружитель, который помимо порогового устройства включает в себя оптимальный фильтр, который ослабляет помехи. Обнаружитель состоит из следующих блоков: согласованный фильтр (1), линейный детектор (2), пороговое устройство (3).
Рисунок 4 – Структура оптимального обнаружителя
Формула вероятности правильного обнаружения простейшего обнаружителя Неймана Пирсона:
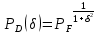
В оптимальном обнаружителе используется фильтр:
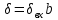
Вероятность правильного обнаружения сигнала оптимального обнаружителя равна:
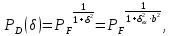
где
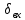- отношение сигнал/помеха на входе фильтра.Вероятность перебраковки
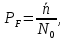
где в числителе стоит среднее количество ложных регистраций определяется из трансцендентного уравнения:
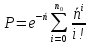
Так как
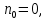то 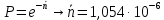Рассчитаем вероятность ложной тревоги, зная по исходным данным N0 = 106:
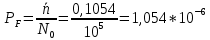
Рисунок 5- Нахождение среднего количества ложных регистраций
На рисунке 6 изображены характеристики обнаружения для оптимального обнаружителя и для обнаружителя Неймана-Пирсона.
Рисунок 6- Зависимость вероятности правильного обнаружения от отношения сигнал/помеха на входе приемного тракта
ЗАКЛЮЧЕНИЕ
Максимально допустимое значение параметра
, если ультразвуковойдефектоскоп должен раздельно принимать сигналы от дефектов, отстоящих по глубине на 3 мм по стали, составляет 1,457 мкс.
Исходя из того, что
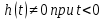, можно сделать вывод, что построение согласованного фильтра невозможно. Нами был построен квазиоптимальный фильтр, состоящий из 1 колебательного контура, близкий по отношению сигнал/помеха к согласованному. Ширина полосы пропускания фильтра составляет 0,216 МГц. Оптимальное значение добротности составляет 23,001, а значение коэффициента b= 1,607.
Определили зависимость
на выходе приёмного тракта, при этомсреднее количество ложных регистраций 0,1054, вероятность перебраковки
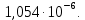
СПИСОК ИСПОЛЬЗОВАННЫХ
ИСТОЧНИКОВ
-
А. Б. Сергиенко. Цифровая обработка сигналов: Учеб. Пособие/ЛЭТИ., 2011 – М.: Высшая Школа, 1979/1991. -
Н. А. Быстрова, Д. Д. Добротин, Е. Л. Шейнман, Анализ и обработка сигналов: Учеб. Пособие/ЛЭТИ.Л., 2018. -
Д. Д. Добротин, Н.А. Зайцева, С. И. Коновалов. Обработка случайных сигналов:Учеб. пособие/ЛЭТИ. Л., 2016 -
Добротин Д. Д., Пигулевский Е. Д. Случайные сигналы и помехи в
системах интроскопии: Учеб.пособие / ЛЭТИ. Л., 1990.
Приложение А
l = 3*10^-3;
c = 5940;
tao = (2.*l)/c;
% Определение длительности сигнала
tao_0 = tao/-log(0.5);
% Построение графика импульсной характеристики
Sp = @(t) (exp(-t./tao_0) .* heaviside(t))
» t_0=1.678e-06;
» tao_0=1.4573e-06;
» t = -3 * t_0 : t_0 / 100 : 3 * t_0;
» plot(t, Sp(t_0-t))
» title('График ИХ')
» xlabel('t,mkc')
» ylabel('h(t)')
f0 = 5e6;
w0 = 2*pi*f0;
deltaw = 2*pi*5e6;
n = 1; %число несвязанных колебательных контуров
P = 0.9; %Доверительная вероятность
n0 = 0; %Число ложных срабатываний
N0 = 1e5;%число импульсов
l = 3e-3;%разрешающая способность
tau0 =1.4573e-06;
t0 = (tau0/2)*log(10);
syms w
J = tau0/(1-1i*(w-w0)*tau0)*exp(-1i*w*t0);
Phr = double(vpaintegral(abs(log(abs(J)))/(1+w^2),w,[-inf inf])) %Проверка условия физической реализуемости фильтра
tau0 =1.4573e-06;
t0 = (tau0/2)*log(10);
syms y omega
F = tau0/(1+1i*omega*tau0);
X = int(abs(F)^2,omega,[0 y])/int(abs(F)^2,omega,[0 deltaw/2]);
y = solve(X-0.9,y);
fprintf('Верхний предел y = %f рад/c\n', y);
syms Q Po Fi
K = 1/sqrt(1+(2*omega*Q/w0)^2)^n;
Fi = -n*atan(2*omega*Q/w0);
Po = abs(vpaintegral(abs(F)*K*cos(omega*t0+angle(F)+Fi),omega,[0 y]))/sqrt(vpaintegral(abs(F)^2, omega, [0 y])*vpaintegral(K^2, omega, [0 y]));
q = 0.001:1:100;
r =(subs(Po, {Q}, {q}));
plot(q, r);
grid on;
xlabel('Q');
ylabel('Po(Q)');
hold off;
[m_ro, idx] = max(r);
Qmax = q(idx);
fprintf('Qmax = %f \nПроигрыш = %f %% \n', Qmax, (1-m_ro)*100);
fprintf('p=%f\n', p);
b = 1.607;
Pf = 0.1054/N0;
delta = 0:0.1:10;
P = Pf.^(1./(1+b^2*delta.^2));
Ph = Pf.^(1./(1+delta.^2));
figure
plot(delta, P);
grid on;
xlabel('\delta');
ylabel('p(\delta)');
hold on;
plot(delta, Ph, 'r--')
legend('Оптимальный обнаружитель', 'Обнаружитель Неймана-Пирсона');