Файл: Исследование свободных процессов электрических цепях.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 108
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра Электронных приборов и устройств
отчет
по лабораторной работе №3
по дисциплине «Теоретические основы электротехники»
Тема: Исследование свободных процессов электрических цепях
| Студенты гр. 1207 | | Бачевский И.М |
| | | Базилов Б. Омурбеков А. |
| Преподаватель | | Козулина Т.П. |
Санкт-Петербург
2023
Цель работы: изучение связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости; экспериментальное определение собственных частот и добротности RLC-контура по осциллограммам.
Схема установки:
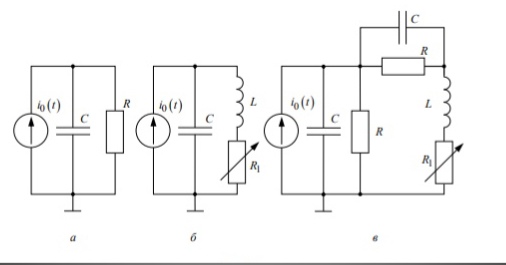
Рис. 1 Схема установки исследования свободных процессов электрических цепях: а – первого порядка, б – второго порядка, в – третьего порядка.
Обработка результатов эксперимента
3.2.1. Исследование свободных процессов в цепи первого порядка
Теоретическая собственная частота цепи
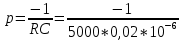=10-4
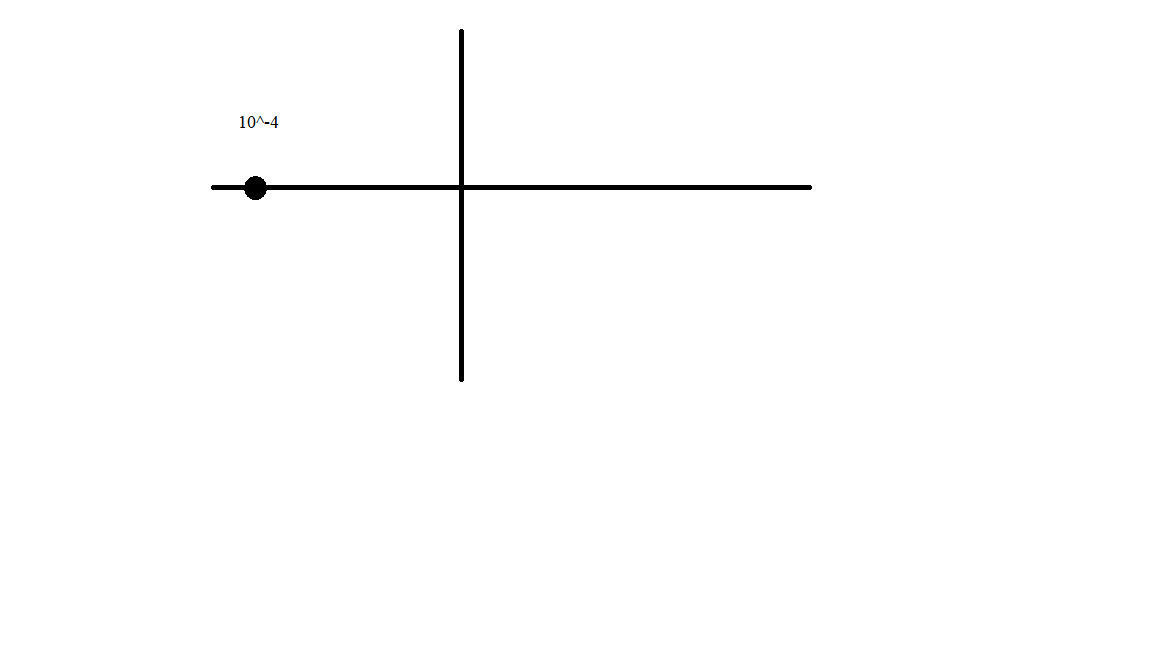Рис. 1 Диаграмма расположения собственной частоты цепи первого порядка.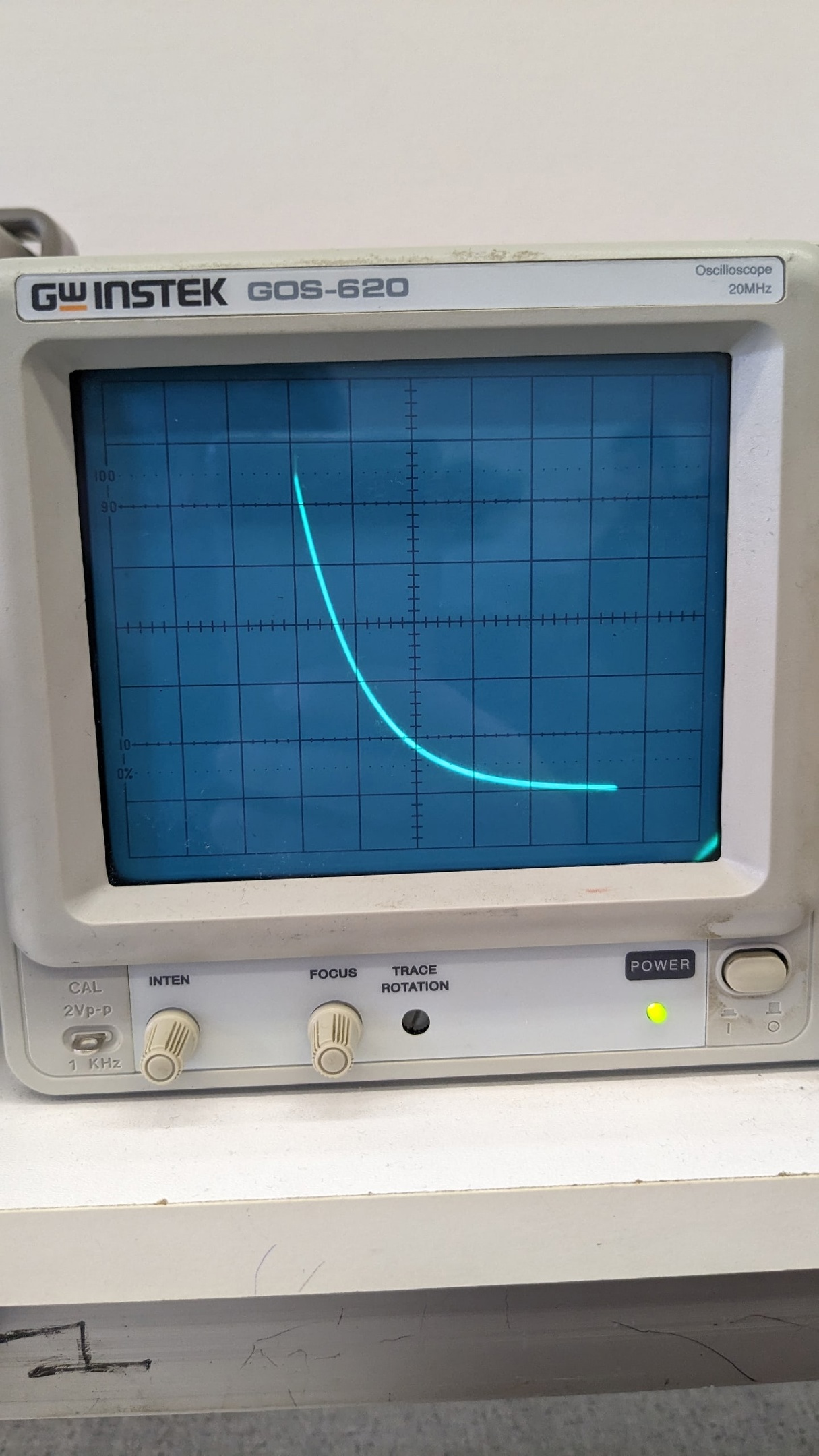
Рис 2. Осциллограмма свободного процесса в цепи первого порядка
; 
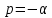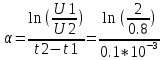
= 9162, 90732 c
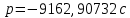
3.2.2 Исследование свободных процессов в цепи второго порядка
Колебательный режим:
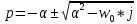
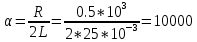
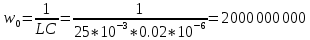
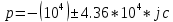
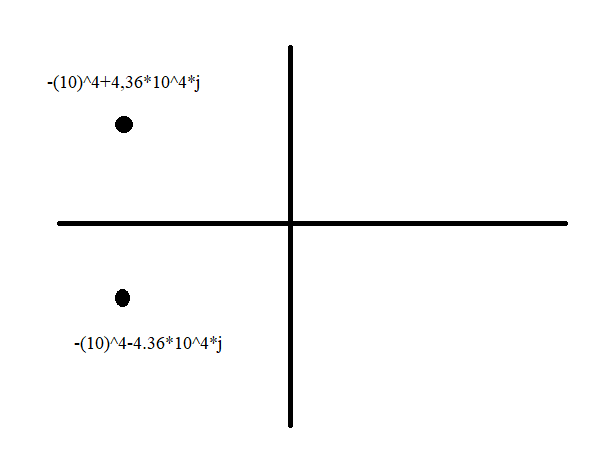
Рис 3. Диаграмма расположения собственной частоты в цепи второго порядка. Колебательный режим.
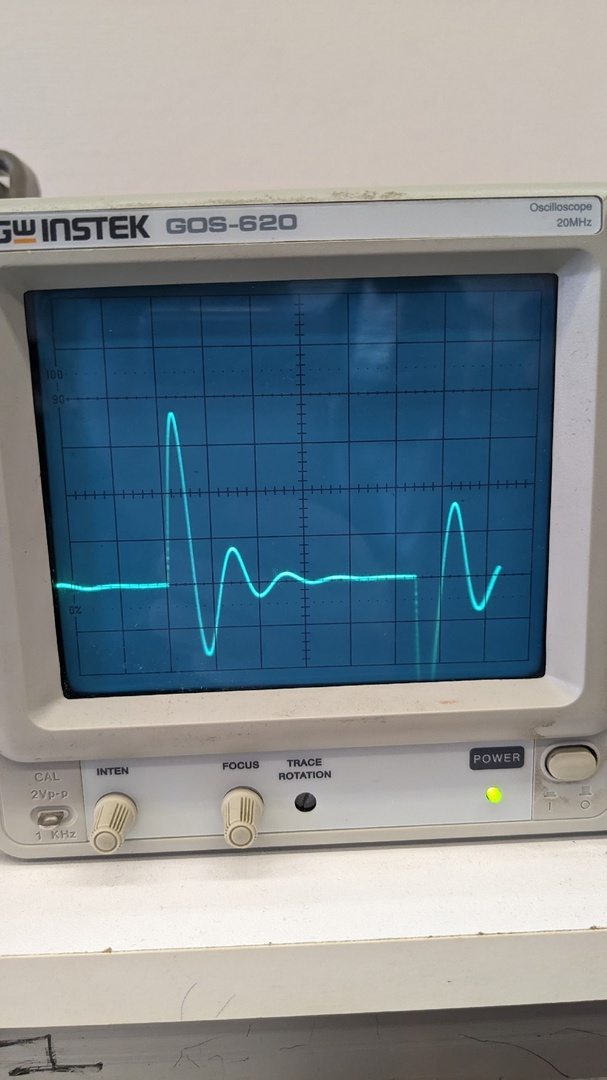
Рис. 4 Осциллограмма колебательного процесса в цепи второго порядка
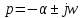
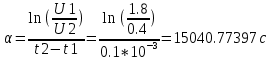
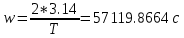
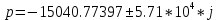cАпериодический режим:
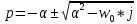
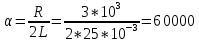
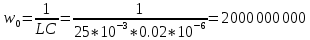
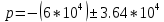c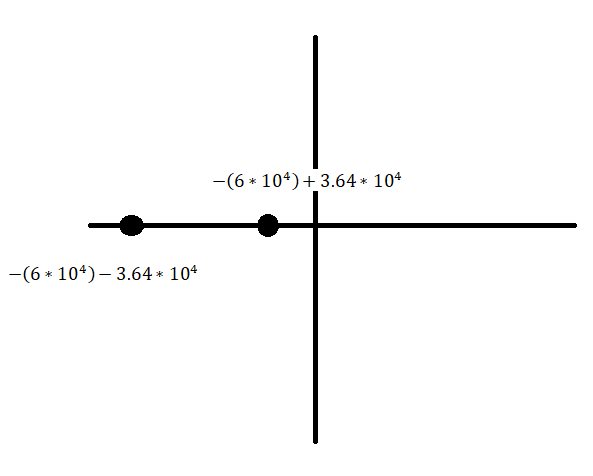
Рис. 5 Диаграмма расположения собственной частоты в цепи второго порядка. Апериодический режим
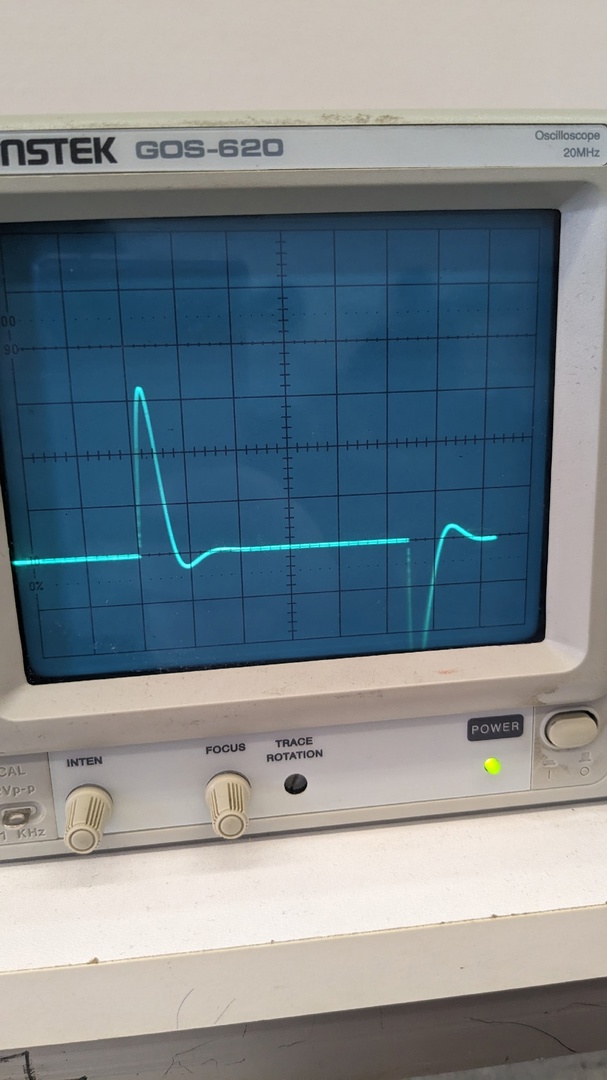
Рис.6 Осциллограмма апериодического режима
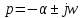
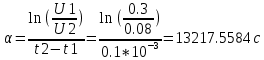
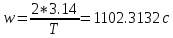
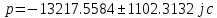
Критический режим:
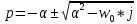
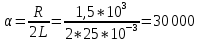
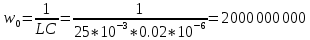
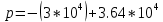
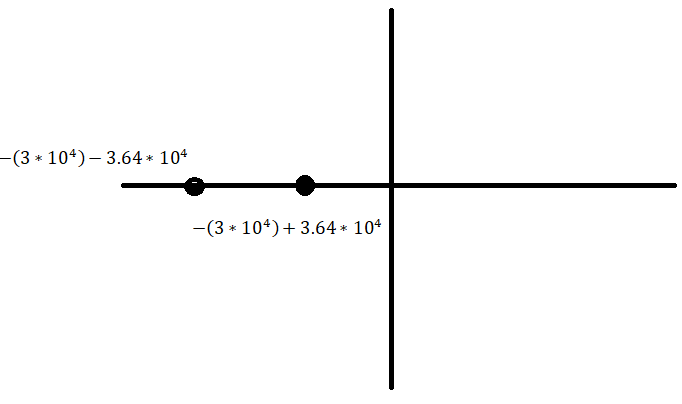
Рис. 7 Диаграмма расположения собственной частоты в цепи второго порядка. Критический режим.
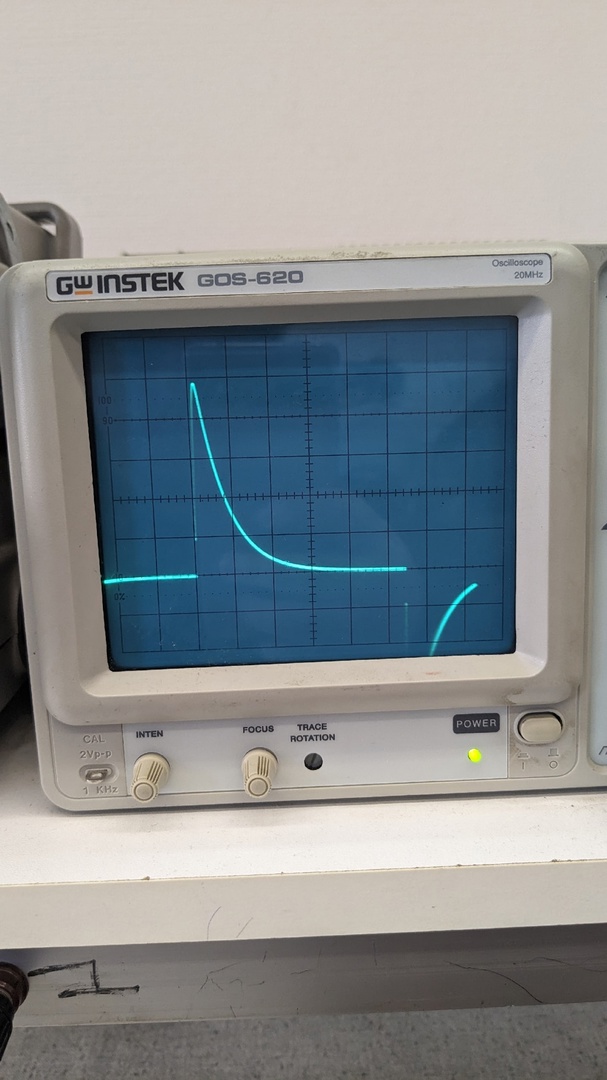
Рис. 8 Осциллограмма критического режима
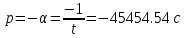
Собственная частота цепи по осциллограмме различается от действительной теоретической на относительно малую величину, что говорит о неверных значениях сопротивления на переменном резисторе.
Добротность контура при R=0.5 kOm
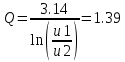
Добротность при R=0 Om
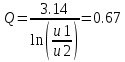
Расчет теоретического значения собственной частоты контура для цепи третьего порядка
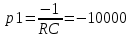
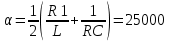
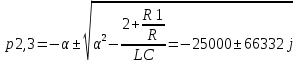
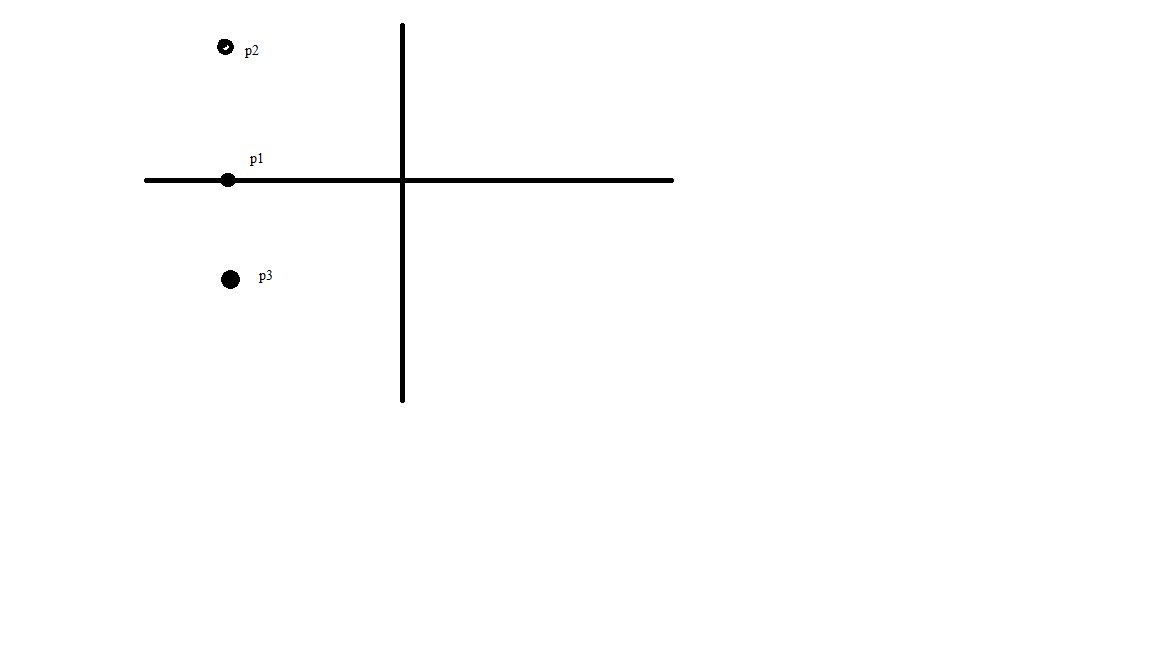
Рис. 9 Диаграмма расположения собственной частоты в цепи третьего порядка
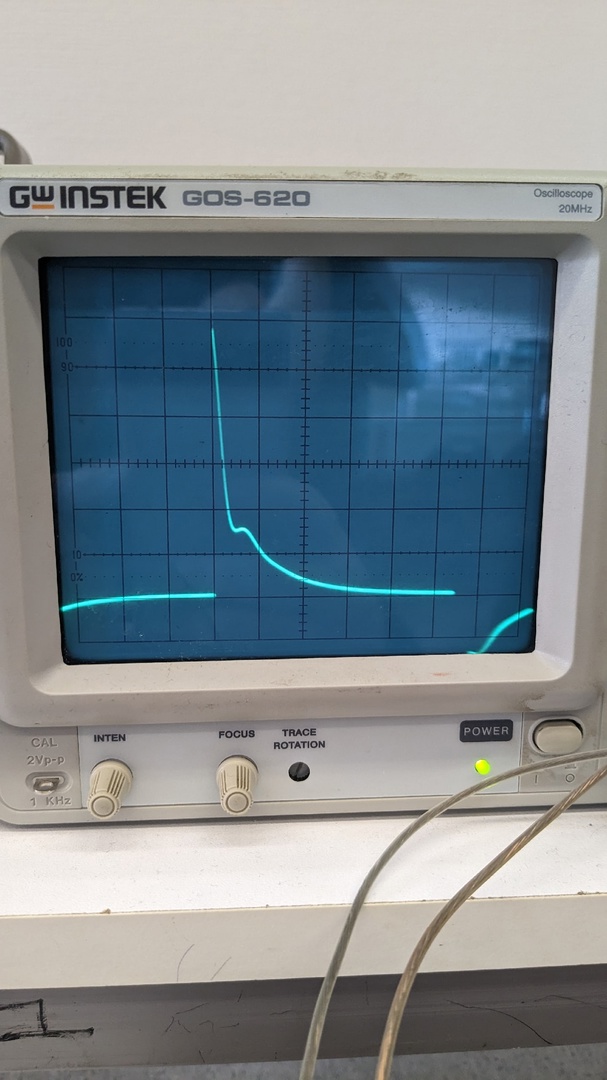
Рис.10 Осциллограмма цепи 3 порядка
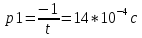
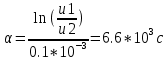
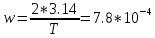
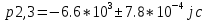
Контрольные вопросы:
1. Uc = Ae-10000t .
2. С большой погрешностью, но соответствуют.
3. U(t) = ∑
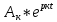
4. Найденные собственные частоты сильно отличаются от выполненного теоретического расчета. Что может быть вызвано износом RLC-компонентов или исследуемой схемы.
6. Теоретическая добротность контура при R1 = 0.5 кОм: Q= 0,2236
Теоретические добротности процессов колебательного режима при R1 = 0.5 кОм не совпадают с экспериментальными в связи с износом исследуемой схемы, но соответствуют протекающим процессам. Для колебательного процесса: Q>0.5
Вывод: Проведено связи между видом свободного процесса в электрической цепи и расположением ее собственных частот (корней характеристического уравнения) на комплексной плоскости. Составлены диаграммы расположения собственных частот цепи на комплексной плоскости, обработаны осциллограммы свободных процессов в цепях. Большинство теоретических выкладок далеки от значений, найденных экспериментально. Так как в формулах расчета теоретических значений переменными являются значения индуктивности, емкости и сопротивления исследуемых элементов, можно судить что различия в значениях собственной частоты вызваны отличием действительного значения характеристик этих элементов от используемых при экспериментальных исследованиях. Так как практически все исследуемые процессы соответствуют теоретическим, но расходится только по значениям частот.