Файл: Отчет по расчётнографической работе 3 По дисциплине Логические основы цифровых систем управления.docx
Добавлен: 05.12.2023
Просмотров: 45
Скачиваний: 5
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
Некоммерческое акционерное общество
«АЛМАТИНСКИЙ УНИВЕРСИТЕТ ЭНЕРГЕТИКИ И СВЯЗИ ИМЕНИ ГУМАРБЕКА ДАУКЕЕВА»
Кафедра Электрических машин и электропривода
ОТЧЕТ
по расчётно-графической работе №3
По дисциплине: Логические основы цифровых систем управления
Тема: Синтез логических схем
Специальность: Электроэнергетика
Выполнил: Группа:
Принял:Мустафин М. А.
Алматы 2023
3 Расчетно - графическая работа №3. Синтез логических схем
3.1 Задание на расчетно - графическую работу
По словесному описанию технологического процесса составить аналитическое описание (логическую функцию) и логическую схему. Минимизировать логическую функцию с помощью карты Карно и составить схему в булевом базисе (с использованием только элементов И, ИЛИ, НЕ) и в базисах И-НЕ, ИЛИ-НЕ.
3.2 Методические указания к расчетно - графической работе
Разработка логической схемы по её аналитическому описанию имеет название задачи синтеза логической схемы [1,4,7].
3.2.1 Разработка логической схемы начинается с определения логической функции, которую должна реализовать логическая схема. Первым шагом является построение таблицы истинности логической схемы по методике, использованной в расчетно - графической работе № 1.
3.2.2 На основании полученной таблицы истинности составляем логическую функцию. Минимизацию булевой функции проводим методом Карно.
Для примера минимизируем логическую функцию трех переменных:
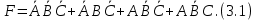
а) Строим таблицу истинности функции F:
Таблица 3.1
| A | B | C | F |
| 0 | 0 | 0 | 1 |
| 0 | 1 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 0 | 1 | 0 |
| 0 | 1 | 1 | 0 |
| 1 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 |
б) Заданную функцию представим с помощью карты Карно:
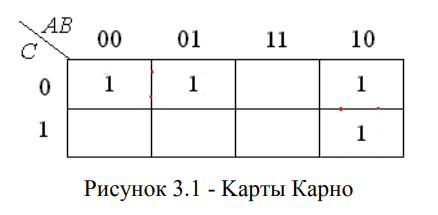
с) Затем производится объединение 2-х, 4-х или 8-ми единиц (рисунок 3.2). В данном случае объединение двух единиц по горизонтали соответствует операции склеивания, в результате которой исключается переменная B:
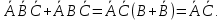
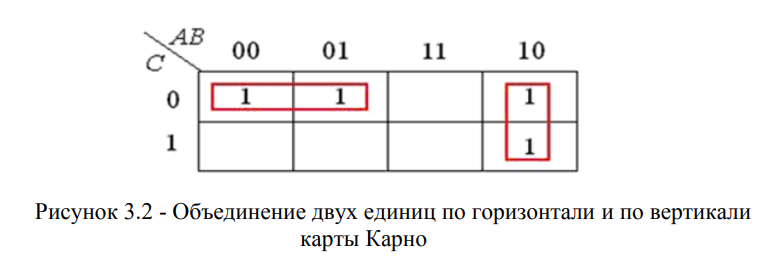
Объединение двух единиц по вертикали соответствует операции склеивания, в результате которой исключена переменная С:
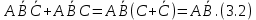
d) Следовательно, минимальная форма заданной функции примет следующий вид:
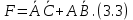
3.1.3 Первая схема проектируется в Булевом базисе (И, ИЛИ, НЕ). Каждой дизъюнкции (логической сумме) соответствует элемент "ИЛИ", число входов которого определяется количеством переменных в дизъюнкции. Каждой конъюнкции (логическому произведению) соответствует элемент "И", число входов которого определяется количеством переменных в конъюнкции. Каждому отрицанию (инверсии) соответствует элемент "НЕ".
Для построения логической схемы необходимо элементы, реализующие логические операции, указанные в выходной функции, располагать в порядке, заданной этой функцией. Например, из выражения
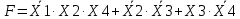(3.4)видно, что понадобятся 4 схемы "НЕ", одна трёхвходовая схема "И", 2 двухвходовые схемы "И" и одна трёхвходовая схема "ИЛИ". В соответствии с этим получаем логическую схему, изображенную на рисунке 3.1:
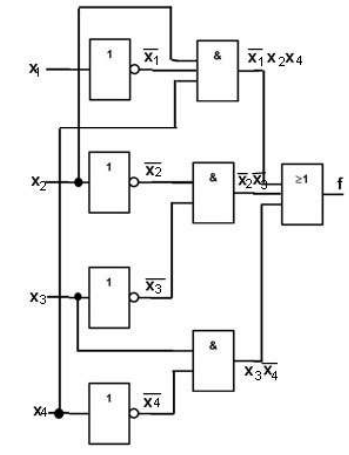
Рисунок 3.3
3.1.4 Часто для сокращения числа микросхем используют элементы "ИНЕ" или/и "ИЛИ-НЕ". Рассмотрим примеры, как построить схему, реализующую ту же функцию (3), но, сначала в базисе "И-НЕ", а затем в базисе "ИЛИ-НЕ".
В качестве примера построим в базисе "И-НЕ" логическую схему, реализующую функцию алгебры логики .
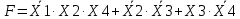
Для этого логическая функция должна быть приведена к виду, содержащему только операции логического умножения (конъюнкции) и инвертирования (отрицания). Это делается при помощи двойного инвертирования исходного выражения функции и применения закона де Моргана:
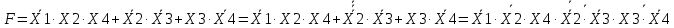(3.5)Для построения логической схемы потребуются 8 схем «И-НЕ». Получаем логическую схему, изображенную на рисунке 3.2.
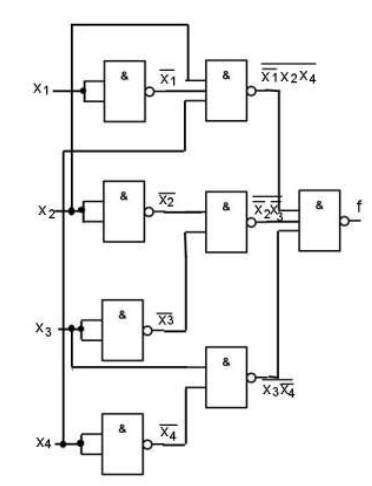
Рисунок 3.4
3.1.5 Построим логическую схему, реализующую функцию алгебры логики
. В базисе «ИЛИ-НЕ». Логическая функция должна быть приведена к виду, содержащему только операции логического сложения (дизъюнкции) и инвертирования (отрицания). Это делается также при помощи двойного инвертирования исходного выражения функции и применения закона де Моргана:
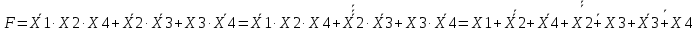(3.6)Для построения логической схемы потребуются 8 схем "И-НЕ". Получаем логическую схему, изображенную на рисунке 3.3.
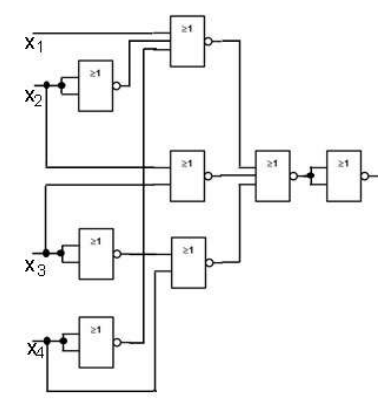
Рисунок 3.5
Решения РГР-3
Таблица 3.2 – Мой вариант заданий на расчетно-графическую работу №3
| X | Y | Z | F1 |
| 1 | 1 | 1 | 0 |
| 1 | 1 | 0 | 0 |
| 1 | 0 | 1 | 0 |
| 1 | 0 | 0 | 1 |
| 0 | 1 | 1 | 1 |
| 0 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 0 | 0 | 0 | 1 |
Моя функция из таблицы будет выглядеть следующим образом:
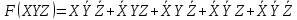
Приступим к упрощению этой функции.
Первым делом я добавил связку
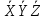, поскольку эта связка и так присутствует в исходной формуле то повторение этой связки нечего не изменить:
Потом использую «переместительный» и «распределительный» закон вынесу повторившиеся элементы за скобки:
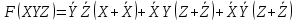
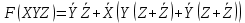
Потом по правилу «операция переменной с её инверсией» убираем всё лишнее:
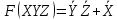
Заданную функцию представим с помощью карты Карно:
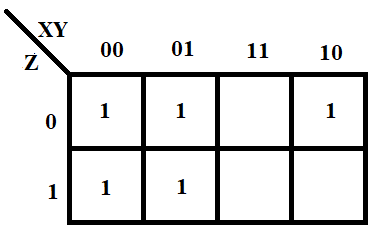
Рисунок 3.6 – Карта Карно
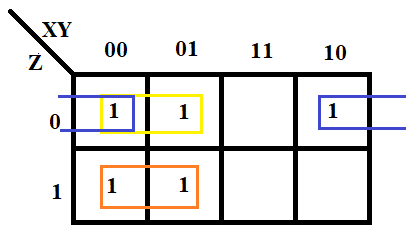
Рисунок 3.7 – Карта Карно объединение по 2 единицам по горизонтали
Начинаем объединение по двум единицам по горизонтали соответствует операции склеивания:
1)
2)
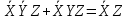
3)
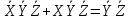
1 и 2 функцию можно еще раз упростить, используя склеивание
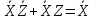
Следовательно, итоговая форма заданной функции примет следующий вид
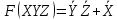
Построим схему используя элементы «И», «ИЛИ», «НЕ». Для изначальной функции
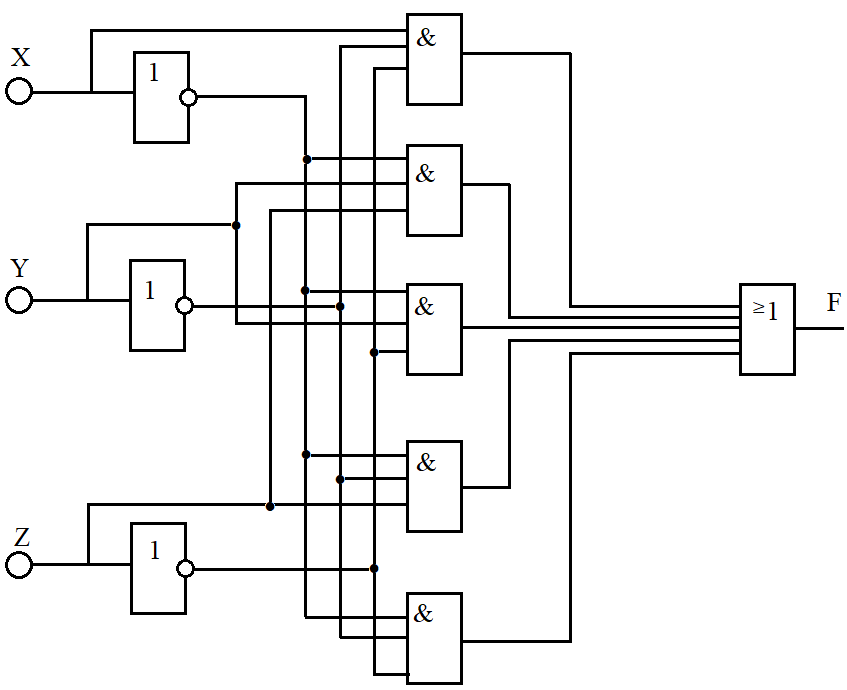
Рисунок 3.8 – Схема состоящих из элементов «И», «ИЛИ», «НЕ».
Построим схему используя элементы «И-НЕ»
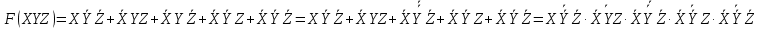
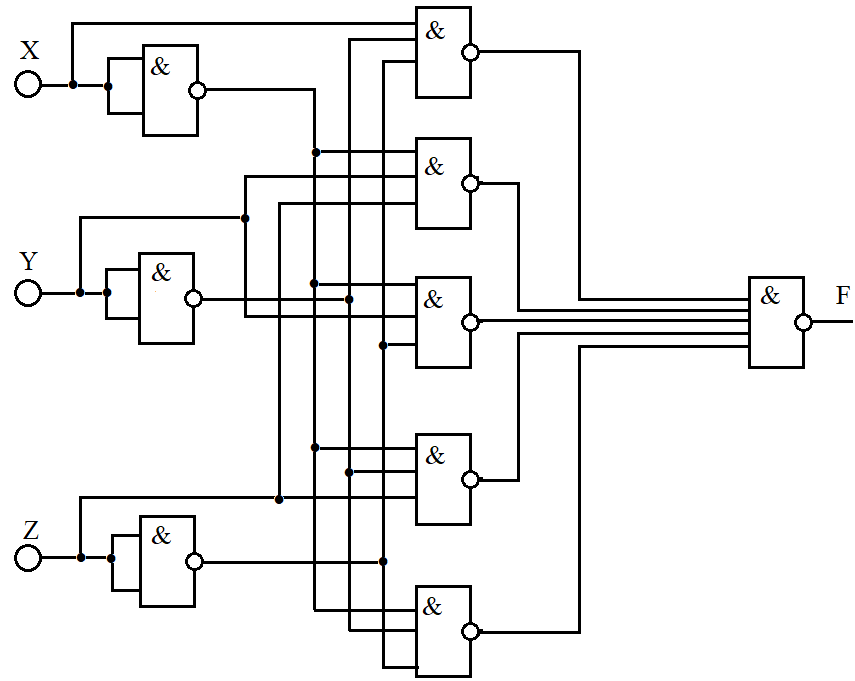
Рисунок 3.9 – Схема состоящий из элемента «И-НЕ»
Построим схему используя элементы «ИЛИ-НЕ»
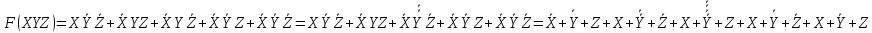
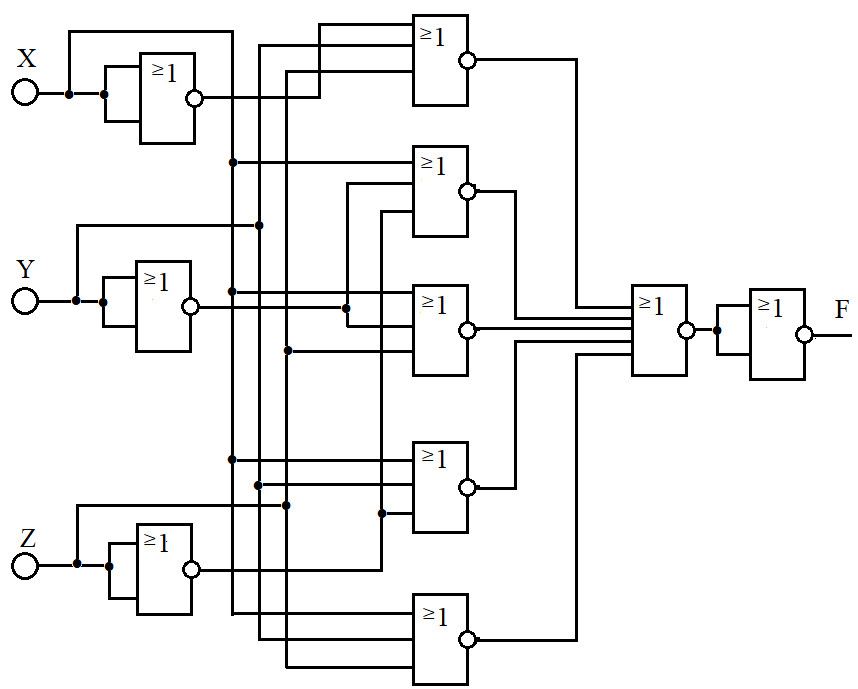
Рисунок 3.10 – Схема состоящий из элемента «ИЛИ-НЕ»