ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 26
Скачиваний: 1
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ
Цели: ввести понятие вписанной окружности и описанного около окружности многоугольника; рассмотреть теорему о том, что в любой треугольник можно вписать окружность.
Ход урока
I. Проверка домашнего задания.
Выполнить устно:
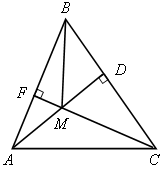 | 1) а) Докажите, что  АВМ == МСА.б) АМ = 4, МD = 3, ВD = 4. Найдите расстояние от точки М до стороны АС. | ||
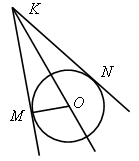 | 2) Найдите 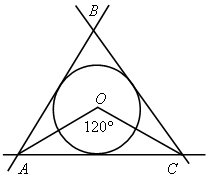МKN и расстояние MN, если ОМ =  , KМ = 3. | ||
| 3) Найдите углы  АВС, если ОАС = 20° и АОС = 120°. | |||
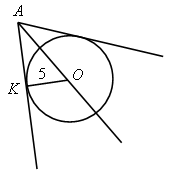 | 4) стороны угла А касаются окружности радиуса r с центром О. а) Найдите ОА, если r = 5 см, А = 60°. | ||
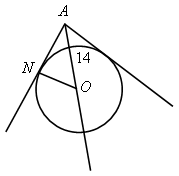 | б) Найдите r, если ОА = 14 дм, А = 90°. | ||
II. Изучение нового материала.
Изложить в виде лекции п. 74 до замечания 2.
III. Закрепление изученного материала.
Выполнить №№ 701 (для остроугольного треугольника), 689, 691.
№ 689.
Решение
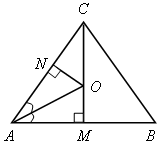 | 1) Центр О вписанной окружности искомого радиуса r лежит на биссектрисе СМ треугольника АВС, а так как СМ  АВ, то вписанная окружность касается отрезка АВ в точке М. Поэтому ОМ = r. |
Далее обсудить с учащимися различные способы решения этой задачи:
I способ.
1. АМ =
AB = 5 см.2. M и N – точки касания, следовательно, AN = АМ = 5 см, откуда CN = АС – АN = 8 cм.
3. В
АСМ : СМ = 
= 12 (см).4. В
СON : СО2 = СN2 + ON2, то есть (12 – r)2 = 82 + r2
144 – 24r + r2 = 64 + r2.
r = 3
.ОМ = ON = 3
см.II способ.
1. В
АСМ : АМ = AB = 5см.СМ =
= 12 (см).2. Отрезок АО – биссектриса треугольника АМС (так как о – центр вписанной окружности), поэтому
или 
; 13r = 60 – 5r, r = 3
.ОМ = ОN = 3
см.IV. Итоги урока.
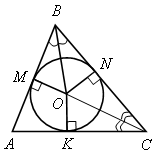 | 1) Центр вписанной в треугольник окружности в точке пересечения биссектрис; 2) ОМ = ON = ОK – радиусы вписанной окружности; 3) окружность единственная для данного треугольника. |
Домашнее задание: вопросы 21, 22, с. 188; №№ 701
Стандартный вид числа
Цели: ввести понятие стандартного вида числа; формировать умение его применять при решении задач.
Ход урока
I. Организационный момент.
II. Устная работа.
– Заполните пустые клеточки:
а) 25 =
2; б) 81 = 3
; в) 625 = (52) ;г)
= 3 ; д) (а3)8 = а ; е) х–8 = (х2) ;ж) (у
)14 = у–28; з) (ab2)–6 = a b
; и)
.III. Самостоятельная проверочная работа.
В а р и а н т 1
Упростить выражение:
1) 6х–5у7 · 2,5х7у–6; 3)
;2) 3,2a6b : (0,8a3b–3); 4)
.В а р и а н т 2
Упростить выражение:
1)
; 3) 
;2)
; 4) 
.IV. Объяснение нового материала.
Согласно пункту учебника ввести понятие стандартного вида числа. Вынести на доску запись:
| Стандартный вид числа: а · 10п, где 1 ≤ а < 10, п – целое число, п – порядок числа. |
После этого дать учащимся задание, которое направлено на усвоение данного понятия.
З а д а н и е. Определить, какие из чисел записаны в стандартном виде, а какие – нет. Ответ объяснить:
а) 2,3 · 109; г) 8 · 10–5; ж) –3 · 10–15;
б) 1,23 · 10–11; д) 4,2 · 1005; з) 0,24 · 10–17;
в) 15 · 1014; е) 5,8 · 1023; и) 10 · 104.
После усвоения понятия показать, как оно может быть применено на практике (разобрать примеры на с. 211–212 учебника).
V. Формирование умений и навыков.
1. № 1013 – устно.
2. Представьте в виде степени числа 10 выражение:
а) 1000 · 10–6; д) 0,1 · 100 · 10–5;
б) 10–10 · 10–5; е) 10000;
в) 10–8 : 104; ж) 0,001;
г) (10–2)3; з) 0,01 · 100.
3. № 1014, № 1015 (б, г), № 1016 (б, г, е, з).
Р е ш е н и е
№ 1014.
а) 52000000 = 5,2 · 107.
П р и м е ч а н и е. На этом примере разбираем, что в стандартном виде числа
а · 10п, а
[1; 10). В исходном числе мы перенесли запятую на 7 цифр влево, то есть уменьшили число в 107 раз. Поэтому 52000000 больше 5,2 в 107 раз.б) 2180000 = 2,18 · 106.
в) 675000000 = 6,75 · 108.
г) 40,44 = 4,044 · 101.
д) 0,00281 = 2,81 · 10-3.
П р и м е ч а н и е. На этом примере разбираем, что в исходном числе мы перенесли запятую на 3 цифры вправо, то есть увеличили число в 103 раз. Поэтому 0,00281 меньше 2,81 в 103 раз.
е) 0,0000035 = 3.5 · 10–6.
№ 1015.
б) 117 · 105 = 1,17 · 102 · 105 = 1,07 · 107;
г) 0,06 · 105 = 6 · 10–2 · 105 = 6 · 103.
№ 1016.
б) 6000000 = 6 · 106;
г) 0,85 = 8,5 · 10–1;
е) 0,000282=2,82 · 10–4;
з) 0,042 · 102 = 4,2 · 10–2 · 102 = 4,2 · 100.
4. № 1017.
Р е ш е н и е
Масса Земли равна 6 · 1021 т.
Масса атома водорода равна 1,7 · 10–21 г.
5. № 1018.
Р е ш е н и е
а) 3,8 · 103 (т) = 3,8 · 103 · 103 (кг) = 3,8 · 103 · 106 (г) = 3,8 · 109 (г);
б) 1,7 · 10–4 (км) = 1,7 · 10–4 · 103 (м) = 1,7 · 10–1 · 102 (см) = 1,7 · 10 (см);
в) 8,62 · 10–1 (кг) = 8,62 · 10–1 · 10–3 (т) = 8,62 · 10–4(т);
г) 5,24 · 105 (см) = 5,24 · 105 · 10–2 (м) = 5,24 · 103 (м).
6. Выполните действия. Результат запишите числом в стандартном виде:
а) (2,8 · 105) · (2,5 · 10–7);
б) (5,7 · 104) : (3,8 · 10–3);
в) 6,2 · 10–2 + 4,8 · 10–2.
Р е ш е н и е
а) (2,8 · 105) · (2,5 · 10–7) = (2,8 · 2,5) · (105 · 10–7) = 7 · 10–2.
б) (5,7 · 104) : (3,8 · 10–3) = (5,7 : 3,8) · (104 : 10–3) = 1,5 · 107.
в) 6,2 · 10–2 + 4,8 · 10–2 = 10–2 · (6,2 + 4,8) = 11 · 10–2 = 1,1 · 10–3.
VI. Итоги урока.
В о п р о с ы у ч а щ и м с я:
– Как записывается число в стандартном виде?
– Записаны ли числа 11 · 108 и 0,93 · 10–5 в стандартном виде? Почему?
– Если число записано в стандартном виде, что называется его порядком?
– Для чего на практике применяется запись чисел в стандартном виде?
Домашнее задание: № 1015 (а, в), № 1016 (а, в, д, ж), № 1019, № 1020, № 10226.
Транспортир, градус, алгоритм измерения углов
(п. 42, ч. 1)
Цель: научить давать определение градуса, обозначать его, измерять углы с помощью транспортира.
Ход урока
I. Оргмомент