Задача №1

Работа выхода электрона из лития А=2,5 эВ. Будет ли фотоэффект при освещении лития монохроматическим светом с длиной волны λ=50 нм?

Решение

В задаче рассматривается явление внешнего фотоэффекта. Применительно к

данному явлению закон сохранения энергии выражается формулой Эйнштейна:



h - постоянная Планка ( h = 6,62 ⋅10^-34Дж·с)

Формула указывает, что энергия фотона при фотоэффекте расходуется на работу по

вырыванию электрона с поверхности металла и сообщение ему кинетической энергии.

Для красной границы фотоэффекта Umax=0. Поэтому выполняется условие

,следовательно,

Произведя вычисления, найдем

Следовательно, фотоэффекта не произойдет.

Задача №2

Электрон пролетает через щель шириной l=1 мкм. С какой наименьшей погрешностью в момент пролета щели может быть определена составляющая импульса электрона на ось Ох?

Решение

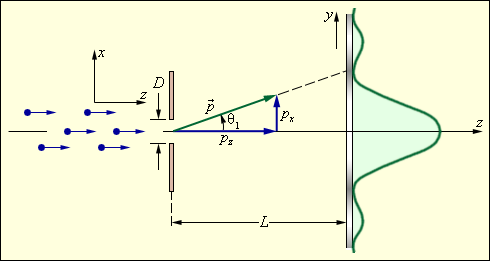
Рассмотрим, например, дифракцию электронов на одиночной щели ширины l (рис. 1).

3

Рисунок 1. Дифракция электронов на щели. График справа – распределение электронов на фотопластинке.

Более 85 % всех электронов, прошедших через щель, попадут в центральный дифракционный максимум. Угловая полуширина θ₁ этого максимума находится из условия

D sin θ1 = λ.

 

Это формула волновой теории. С корпускулярной точки зрения можно считать, что при пролете через щель электрон приобретает дополнительный импульс в перпендикулярном направлении. Пренебрегая 15 % электронов, которые попадают на фотопластинку за пределами центрального максимума, можно считать, что максимальное значение p_y поперечного импульса равно

---

где p – модуль полного импульса электрона, равный, согласно де Бройлю, h / λ. Величина p при прохождении электрона через щель не меняется, т. к. остается неизменной длина волны λ. Из этих соотношений следует

Квантовая механика вкладывает в это простое на вид соотношение, являющееся следствием волновых свойств микрочастицы, чрезвычайно глубокий смысл. Прохождение электронов через щель является экспериментом, в котором y – координата электрона – определяется с точностью Δy = D. Величину Δy называют неопределенностью измерения координаты. В то же время точность определения y – составляющей импульса электрона в момент прохождения через щель – равна p_y или даже больше, если учесть побочные максимумы дифракционной картины. Эту величину называют неопределенностью проекции импульса и обозначают Δp_y. Таким образом, величины Δy и Δp_y связаны соотношением

Δy · Δpy ≥ h,

которое называется соотношением неопределенностей Гейзенберга. Величины Δy и Δp_y нужно понимать в том смысле, что микрочастицы в принципе не имеют одновременно точного значения координаты и соответствующей проекции импульса. Соотношение неопределенностей не связано с несовершенством применяемых приборов для одновременного измерения координаты и импульса микрочастицы. Оно является проявлением двойственной корпускулярно-волновой природы материальных микрообъектов. Соотношение неопределенностей позволяет оценить, в какой мере можно применять к микрочастицам понятия классической механики. Оно показывает, в частности, что к микрообъектам неприменимо классическое понятие траектории, так как движение по траектории характеризуется в любой момент времени определенными значениями координат и скорости. Принципиально невозможно указать траекторию, по которой двигался какой-то конкретный электрон после прохождения щели и до фотопластинки в рассмотренном мысленном эксперименте. 

---

Смотрите также файлы

• Рабочая программа преддипломной практики опоп по специальности 43. 02. 11 Гостиничный сервис Заочная форма обучения 2018 г.doc

• Фисташковый торт.docx

• 1 изучить нормативнотехническую документацию по теме.docx

• Исследование коэффициента мощности систем электроснабжения промпредприятия по курсу Электроснабжение Тема Внутризаводское электроснабжение Цели работы Уяснение цели повышения коэффициента мощности на предприятии.docx

• Тема Короткие замыкания в системах электроснабжения.docx