Файл: Цель выполнения контрольнокурсовой работы. По окончании курса Общая теория измерений.docx

Скачать файл
Заказать решение

ВУЗ: Не указан

Категория: Курсовая работа

Дисциплина: Не указана

Добавлен: 05.12.2023

Просмотров: 29

Скачиваний: 5

ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.


Цель выполнения контрольно-курсовой работы.

По окончании курса «Общая теория измерений» студент должен знать и уметь использовать методики обработки результатов различных видов измерений, в том числе многократных равноточных измерений, характерных для метрологических работ. Данная контрольно-курсовая работа имеет целью:

  • закрепить навыки определения точечных оценок и исключения грубых погрешностей;

  • выработать умение строить гистограмму, производить проверку гипотезы о нормальности закона распределения вероятности, пользуясь таблицами нормального распределения и распределения c2;

  • выработать умение правильной оценки результата измерений в виде доверительного интервала.

  • углубить и закрепить знания по курсу;

  • развить навыки самостоятельной работы с научной и справочной литературой, нормативными документами, материалами, опубликованными в периодической печати и др.;

  • приобрести опыт их творческого использования;

  • развить умение связывать теоретические положения с условиями современной практики;


Задание

Вариант 7

Результаты измерений

30.46 30.28 29.88 30.00 30.12 30.24 30.18 30.32 30.10 30.62 30.31 30.28 29.93 30.14 30.03 30.35 30.15 30.15 30.18 29.77 30.00 30.11 30.00 29.98 30.09 30.19 29.63 30.34 30.09 29.92 29.99 29.78 30.02 30.39 29.89 29.97 30.21 29.84 29.85 30.09 29.74 30.07 30.09 30.01 30.28 30.04 30.36 30.06 30.08 30.40 29.89 29.95 30.37 29.90 30.38 30.32 29.83 30.12 30.08 30.09 30.43 29.75 30.22 30.10 30.08 29.73 30.08 30.10 29.96 30.19 30.39 29.84 30.24 30.10 30.05 29.84 30.30 29.96 30.11 29.79 29.93 30.28 29.93 30.36 29.98 30.32 30.09 30.44 30.11 29.87 30.53 29.79 30.21 30.00 29.98 29.76 30.16 29.97 30.16 30.09

Определить вид ЗРВ по критерию Пирсона;

Записать результат с доверительной вероятностью P= 0.97

Результаты измерений

44.44 44.17 44.10 44.22 44.02 44.30 44.11 44.26 44.06 44.18 44.16 44.21 44.06 44.16 43.93 44.18 44.05 44.22 44.08 43.97 44.22 44.23 44.32 44.21 44.07 44.28 44.10 44.22 44.16 44.15 44.43 44.43 44.41 44.11 44.15 44.07 44.11 44.28 44.49 44.14 44.19 44.34 44.09 44.19 44.11 44.13 44.20 44.09 44.03 44.03 44.18 44.29 44.12 44.24 44.23 44.37 44.11 44.26 44.24 44.11 44.21 44.25 44.12 44.05 44.09 44.18 44.10 44.06 44.28 44.36 44.26 44.23 44.17 44.09 44.07 44.17 44.13 44.01 44.06 44.26 44.27 44.18 44.28 44.21 43.99 44.19 44.07 44.10 44.14 44.21 44.28 44.08 44.39 44.02 44.30 44.16 44.16 44.37 44.09 44.21

Определить вид ЗРВ по критерию Пирсона;

Записать результат с доверительной вероятностью P= 0,96

Для 100 независимых числовых значений результата измерения некоторой физической величины необходимо:

  • проверить гипотезу о нормальности распределения вероятности результатов измерения;

  • записать результат в принятой форме, исходя из уровня доверительной вероятности 0,96;

  • представить два варианта доверительного интервала – для нормального и для неизвестного закона распределения вероятности среднего арифметического значения измеряемого напряжения

Равноточными называются измерения, у которых все значения отсчетов «Xi» имеют одинаковую дисперсию (точность).

Обработка результатов многократных равноточных измерений производится в следующем порядке:

  1. Определение оценок числовых характеристик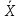 и S закона распределения вероятности результата измерения ( 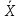и S – среднее арифметическое и оценка среднеквадратического отклонения измеряемой величины соответственно);

  2. Исключение «грубых промахов», если таковые имеются, из результатов измерений и пересчет оценок числовых характеристик закона распределения вероятности результата измерения;

  3. Проверка гипотезы о виде закона распределения вероятности результата измерения (чаще всего проверяется гипотеза о его нормальности);

  4. Представление результата измерения в виде доверительного интервала, соответствующего определенному уровню доверительной вероятности.




Исходные данные

X
m

43,93
1

43,97
1

43,99
1

44,01
1

44,02
2

44,03
2

44,05
2

44,06
4

44,07
4

44,08
2

44,09
5

44,1
4

44,11
6

44,12
2

44,13
2

44,14
2

44,15
2

44,16
5

44,17
3

44,18
5

44,19
3

44,2
1

44,21
6

44,22
4

44,23
3

44,24
2

44,25
1

44,26
4

44,27
1

44,28
5

44,29
1

44,3
2

44,32
1

44,34
1

44,36
1

44,37
2

44,39
1

44,41
1

44,43
2

44,44
1

44,49
1

Решение:

1. Используя полученные данные, найдем значение среднего арифметического X ср и оценки среднего квадратического отклонения S:

X ср=4417,86/100=44,1786

S=0,1116

2. С помощью правила «трех сигм» проверим наличие грубых промахов:



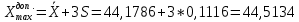
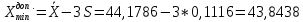
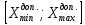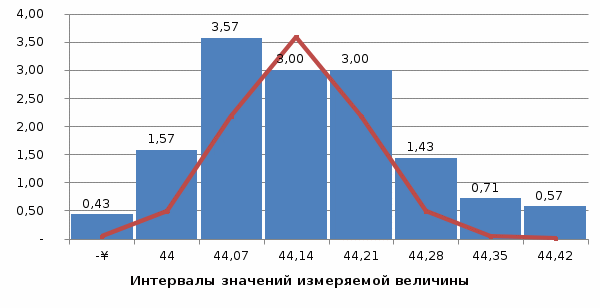
Ни один из результатов не выходит за границы интервала , следовательно, с вероятностью 0,9973 принимается гипотеза об отсутствии грубых промахов.
3. Результаты отдельных измерений расположим в вариационный ряд по возрастанию их численных значений заносим в таблицу 2. Строим гистограмму (рисунок 1).Участок оси абсцисс, на котором располагается вариационный ряд значений физической величины, разбивается на k одинаковых ∆X.

Принимаем k=8

Тогда

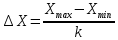
4. Полученное значение округляем до возможно меньшего числа значащих цифр для удобств последующих действий.



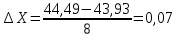
Определим значение аргумента 
zj интегральной функции нормированного нормального распределения:


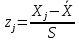
j
Интервал
mj
zj
Ф(zj)
Pj
mj-n Pj
j2

Xj-1
Xj

1

44
3
-1,59932
0,05476
0,05476
-2,47595
1,119504

2
44
44,07
11
-0,97249
0,165247
0,110488
-0,04877
0,000215

3
44,07
44,14
25
-0,34565
0,364717
0,19947
5,053011
1,280039

4
44,14
44,21
21
0,281179
0,610784
0,246066
-3,60665
0,528634

5
44,21
44,28
21
0,908012
0,81822
0,207436
0,256371
0,003168

6
44,28
44,35
10
1,534845
0,937711
0,119492
-1,94916
0,317948

7
44,35
44,42
5
2,161678
0,984733
0,047021
0,297889
0,018872

8
44,42
+
4
+
1
0,015267
2,473258
4,006574









100






1
0
7,274954




  1. Поскольку конец предыдущего интервала является одновременно началом следующего, то теоретическая вероятность попадания результата определится по формуле

.

Началом первого интервала следует считать «–∞», а функции .

  1. По последнему столбцу рассчитаем значение χ2-критерия: χ2 = 7,2749.

  2. Определим табличное (критическое) значение χ2-критерия Пирсона, задавшись доверительной вероятностью, равной 0,96 и вычислив по формуле число степеней свободы: r=k-3

r = 8 – 3 = 5

т2=11,6443, т2>2.

Таким образом, с вероятностью 0,96 гипотеза о нормальности закона распределения вероятности значения физической величины принимается.

5. Представим результаты в виде доверительного интервала с доверительной вероятностью Р = 0,96.

Sx2=0,1116/100=0,01116

  1. Исходя из того, что закон распределения вероятности значений физической величины с вероятностью 0,96 соответствует нормальному, считаем, что, и закон распределения вероятности среднего арифметического тоже соответствует нормальному. Поэтому выбираем параметр t  по таблице нормированного нормального распределения вероятности. Для доверительной вероятности Р=0,96 параметрt=2,08.

Тогда результат измерения запишется следующим образом:

44,1786-2,08*0,1116X44,1786+2,08*0,1116

или с вероятностью Р=0,96

43,95X44,41.

Если же есть основания полагать, что среднее арифметическое имеет неизвестное, отличное от нормального распределение вероятности, то относительную ширину доверительного интервала рассчитаем из неравенства Чебышева: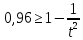





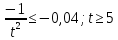
Окончательно результат измерения примет вид:

44,1786-5*0,1116X44,1786+5*0,1116

43,62X44,74.

Построим гистограмму

1. Шишкин, И.Ф. Метрология, стандартизация и управление качеством. Учебник для вузов/ Под ред. Н.С. Соломенко. - М.: Изд-во стандартов, 1990.- 342с.

Смотрите также файлы