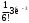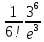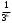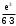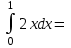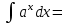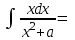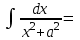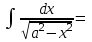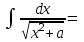Файл: Если функция uf(x,y) имеет непрерывные смешанные производные высших порядков, то справедливо соотношение.docx
ВУЗ: Не указан
Категория: Не указан
Дисциплина: Не указана
Добавлен: 05.12.2023
Просмотров: 86
Скачиваний: 4
ВНИМАНИЕ! Если данный файл нарушает Ваши авторские права, то обязательно сообщите нам.
-
Если функция u=f(x,y) имеет непрерывные смешанные производные высших порядков, то справедливо соотношение…
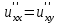 .
.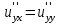 .
.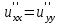 .
.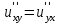 .
.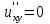 .
.-
Найти 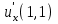 , если
, если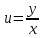 :
:
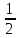 .
.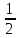 .
.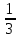 .
.-
Вычислить 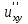 , если
, если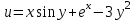 :
:
-
Вычислить 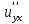 , если
, если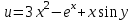 :
:
6.
cosy.
-
Найти 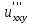 приx=y=1, если
приx=y=1, если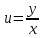 :
:
0.
-
Значение 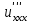 приx=y=1, если
приx=y=1, если 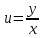 лежит в промежутке
лежит в промежутке
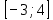
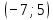
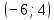
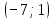
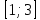
-
Двойным интегралом 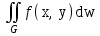 от функции f(x, y) по области G называется:
от функции f(x, y) по области G называется:
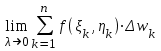 ;
; 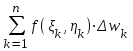 ;
; 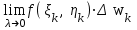 ;
; 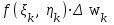 ;
;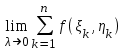 .
.-
По какой области вычисляется интеграл 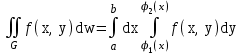 ?
?
-
Вычислить 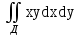 , где Д – прямоугольник
, где Д – прямоугольник 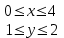 .
.
-
Вычислить 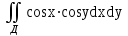 , где Д – квадрат
, где Д – квадрат 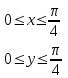 .
.
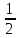 ;
; 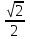 ;
; 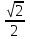 ;
; 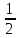 ;
; 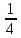 .
.-
Вычислить 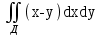 , где Д – прямоугольник
, где Д – прямоугольник 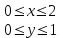 .
.
-
Изменить порядок интегрирования 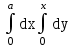 .
.
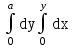 ;
; 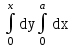 ;
; 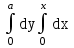 ;
; 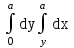 ;
; 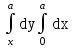 .
.-
Двойной интеграл 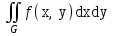 в полярных координатах имеет вид:
в полярных координатах имеет вид:
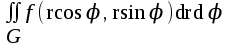 ;
;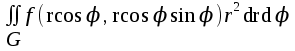 ;
;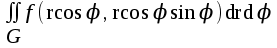 ;
;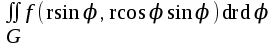
-
Вычислить 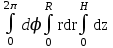 :
:
-
Интеграл 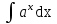 равен:
равен:
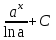 ;
; 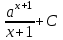 ;
; 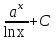 ;
; -
Вычислить 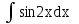 .
.
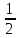 cos2x + C;
cos2x + C; 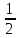 cos2x + C;
cos2x + C; -
Вычислить 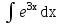 .
.
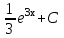 ;
; 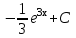 ;
; 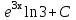 ;
; 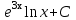 ;
; 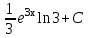 .
.-
Какназываетсявыражение 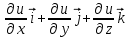 ?
?
-
Каким методом решается интеграл 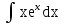 ?
?
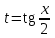 .
.-
Каким методом решается интеграл 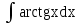 ?
?
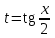 .
.-
Разложение рациональной функции 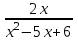 на элементарные дроби имеет вид:
на элементарные дроби имеет вид:
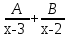 ;
; 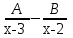 ;
; 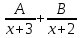 ;
; 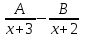 ;
; -
Вычислить 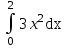 .
.
-
Градиент функции u = x2y2z2 в произвольной точке равен
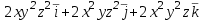
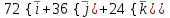 =(72,36,24)
=(72,36,24)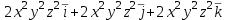
-
Наибольшая скорость возрастания функции (x, y) = x2 – 2xy + 3y при переходе через точку (1, 2) равна
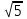
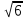
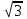
-
Если кривую интегрирования AB разбивать на части AC и CB, то
-
При изменении направления на кривой интегрирования криволинейный интеграл I рода:
-
По формуле 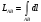 вычисляется:
вычисляется:
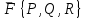 , действующей на точку при перемещении ее по дуге AB
, действующей на точку при перемещении ее по дуге AB-
По формуле 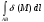 вычисляется:
вычисляется:
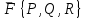 , действующей на точку при перемещении ее по дуге AB
, действующей на точку при перемещении ее по дуге AB-
По формуле 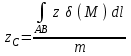 вычисляется:
вычисляется:
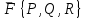 , действующей на точку при перемещении ее по дуге AB
, действующей на точку при перемещении ее по дуге AB-
По формуле 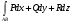 вычисляется:
вычисляется:
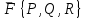 , действующей на точку при перемещении ее по дуге AB
, действующей на точку при перемещении ее по дуге AB-
Двойной интеграл 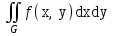 с положительной подынтегральной функцией может быть истолкован физически как:
с положительной подынтегральной функцией может быть истолкован физически как:
-
Двойной интеграл 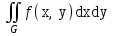 с неотрицательной подынтегральной функцией может быть истолкован геометрически как:
с неотрицательной подынтегральной функцией может быть истолкован геометрически как:
-
Двойной интеграл 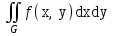 в полярных координатах имеет вид:
в полярных координатах имеет вид:
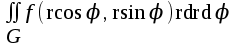 ;
;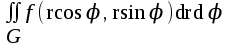 ;
;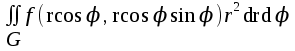 ;
;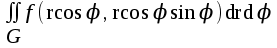 ;
;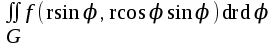
-
Тройным интегралом от функции f(x, y) по области называется:
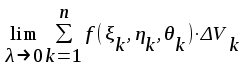 ;
;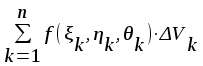 ;
;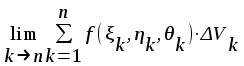 ;
;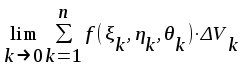 ;
;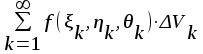
-
Тройной интеграл 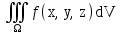 с положительной подынтегральной функцией может быть истолкован физически как:
с положительной подынтегральной функцией может быть истолкован физически как:
-
Формула преобразования тройного интеграла 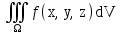 к цилиндрическим координатам имеет вид:
к цилиндрическим координатам имеет вид:
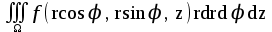 ;
;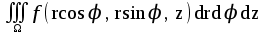 ;
; ;
;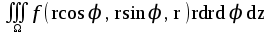 ;
;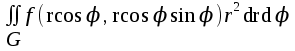
-
Двойной интеграл 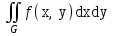 с положительной подынтегральной функцией может быть истолкован физически как:
с положительной подынтегральной функцией может быть истолкован физически как:
-
Двойной интеграл 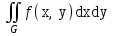 с неотрицательной подынтегральной функцией может быть истолкован геометрически как:
с неотрицательной подынтегральной функцией может быть истолкован геометрически как:
-
Двойной интеграл 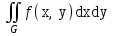 в полярных координатах имеет вид:
в полярных координатах имеет вид:
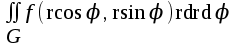 ;
;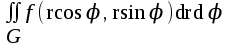 ;
;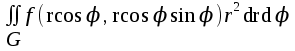 ;
;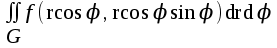 ;
;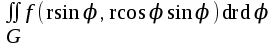
-
Тройным интегралом от функции f(x, y) по области называется:
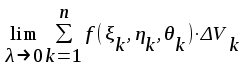 ;
;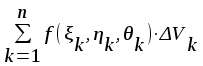 ;
;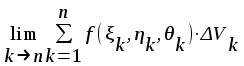 ;
;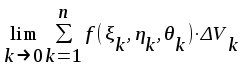 ;
;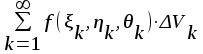
-
Тройной интеграл 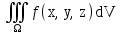 с положительной подынтегральной функцией может быть истолкован физически как:
с положительной подынтегральной функцией может быть истолкован физически как:
-
Формула преобразования тройного интеграла 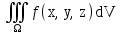 к цилиндрическим координатам имеет вид:
к цилиндрическим координатам имеет вид:
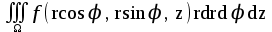 ;
;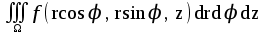 ;
;-
Сумма членов бесконечной числовой последовательности u1, u2, …, un, … или u1 + u2 + … + un + … =  un называется:
un называется:
-
Суммы Sn = u1 + u2 + …+ un =  uk, n = 1, 2 называются:
uk, n = 1, 2 называются:
-
Предел последовательности частичных сумм limSn= S, S =  un называется:
un называется:
-
Ряд  (un + vn), где элементы получены в результате сложения исходных элементов с одинаковыми номерами, называется:
(un + vn), где элементы получены в результате сложения исходных элементов с одинаковыми номерами, называется:
-
Для того, чтобы последовательность а1, а2, … , аn была сходящейся, необходимо и достаточно, чтобы для любого Е > 0 существовал такой номер N, что при n>N и любом p> 0, где p – целое число, выполнялось бы равенство: │an+p - an│
-
Выберитегармоническийряд:
-
Для сходимости ряда  unc неотрицательными членами необходимо и достаточно:
unc неотрицательными членами необходимо и достаточно:
-
Если для ряда  un с положительными членами существует такое число g< 1, что для всех достаточно больших n выполняется неравенство
un с положительными членами существует такое число g< 1, что для всех достаточно больших n выполняется неравенство  g, то ряд
g, то ряд  uncходится, если же для всех достаточно больших n выполняется условие
uncходится, если же для всех достаточно больших n выполняется условие  , то ряд
, то ряд  un расходится. Это признак сходимости:
un расходится. Это признак сходимости:
-
Если для ряда  un с неотрицательными членами существует такое число g< 1, что для всех достаточно больших n выполняется неравенство
un с неотрицательными членами существует такое число g< 1, что для всех достаточно больших n выполняется неравенство  g, то ряд
g, то ряд  un сходится, если же для всех достаточно больших n выполняется неравенство, то ряд
un сходится, если же для всех достаточно больших n выполняется неравенство, то ряд  un расходится. Это признак сходимости:
un расходится. Это признак сходимости:
-
Если существует предел limn→∞  = p, то при p<1 ряд сходится, а при p>1 ряд:
= p, то при p<1 ряд сходится, а при p>1 ряд:

-
Укажите общегармонический ряд:
-
Еслиузнакочередующегосярядаu1 – u2 + u3 – u4 + … + (-1)n+1un + … абсолютные величины u1 убывают u1>u2>u3> … и общий член стремится к нулю un→0, то ряд сходится. Это признак сходимости:
-
Если сходится ряд  │un│, то этот ряд
│un│, то этот ряд  un называется:
un называется:
-
Если существует предел 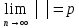 , то при p<1 ряд
, то при p<1 ряд  un будет абсолютно сходящимся, а при p>1 ряд будет расходящимся. При p=1 признак не дает ответа о сходимости ряда. Это признак сходимости:
un будет абсолютно сходящимся, а при p>1 ряд будет расходящимся. При p=1 признак не дает ответа о сходимости ряда. Это признак сходимости:
-
Для абсолютной сходимости ряда  un необходимо и достаточно, чтобы его можно было представить в виде:
un необходимо и достаточно, чтобы его можно было представить в виде:
-
Если членами ряда являются не числа, а функции от х, то ряд называется:
-
Функция Sn (X) =  (x), n = 1, 2 функционального ряда
(x), n = 1, 2 функционального ряда  (х) называется:
(х) называется:
-
Совокупность всех значений х, для которых сходится ряд  (х) называется:
(х) называется:
-
Ряд  (х) сходится равномерно и притом абсолютно на отрезке [a, b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами М1 + М2 + … + Мn… т.е. имеет место неравенство │un (x)│≤ Mn. Это признак равномерной сходимости:
(х) сходится равномерно и притом абсолютно на отрезке [a, b], если модули его членов на том же отрезке не превосходят соответствующих членов сходящегося числового ряда с положительными членами М1 + М2 + … + Мn… т.е. имеет место неравенство │un (x)│≤ Mn. Это признак равномерной сходимости:
-
Равномерно сходящийся на отрезке [a, b] ряд с непрерывными членами можно почленно интегрировать на этом отрезке, т.е. ряд, составленный из интегралов от его членов по отрезку [a, b] сходится к интегралу от суммы ряда по этому отрезку  ; α, β
; α, β  [a, b]. Это теорема о:
[a, b]. Это теорема о:
-
Если члены ряда  сходится на отрезке [a, b] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных
сходится на отрезке [a, b] представляют собой непрерывные функции, имеющие непрерывные производные, и ряд, составленный из этих производных  сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно:
сходится на этом отрезке равномерно, то и данный ряд сходится равномерно и его можно дифференцировать почленно: . Это теорема о:
. Это теорема о:
-
Ряд вида а0 + а1х + а2х2 + … + аnxn + … =  называется:
называется:
-
Если степенной ряд а0 + а1х + а2х2 + … + аnxn + … =  сходится при х=х1, то он сходится и притом абсолютно для всех │х│>│х1│. Это теорема:
сходится при х=х1, то он сходится и притом абсолютно для всех │х│>│х1│. Это теорема:
-
Если ряд  сходится, а
сходится, а  │un│ расходится, то
│un│ расходится, то  называется:
называется:
-
Необходимое условие сходимости выполнено для ряда:
-
Найдите радиус сходимости степенного ряда  :
:
-
Для исследования сходимости ряда 
 надо применить признак :
надо применить признак :
-
Первые три члена ряда  есть числа:
есть числа:
-
Найдите радиус сходимости степенного ряда  :
:
-
Знакопеременный ряд  называется условно сходящимся, если:
называется условно сходящимся, если:
1) ряд
2) ряд
3) оба ряда
4)
-
Среди предложенных вариантов ответа выберите значение площади фигуры, ограниченной линиями  :
:
-
Среди предложенных вариантов ответа выберите значение площади фигуры, ограниченной линиями  :
:
-
Среди предложенных вариантов ответа выберите значение площади фигуры, ограниченной линиями  :
:
;
 ;
; 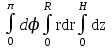 ;
; 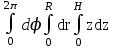
-
Вычислить  :
:
-
Формула преобразования тройного интеграла 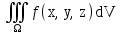 к сферическим координатам имеет вид:
к сферическим координатам имеет вид:
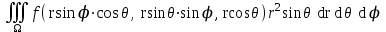 ;
;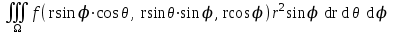 ;
;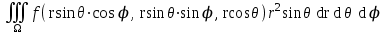 ;
;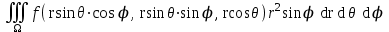 ;
;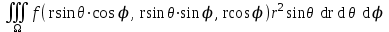
-
Какое выражение называется элементом объёма в сферических координатах?
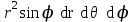 ;
;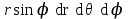 ;
;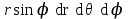 ;
;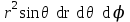 ;
;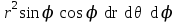 .
.-
Объём шара радиуса R вычисляется по формуле:
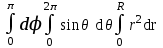 ;
; 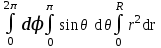 ;
;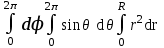 ;
; 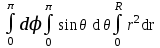 ;
;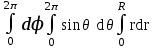
-
Вычислить: 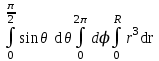 .
.
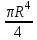 ;
; 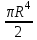 ;
; -
Вычислить 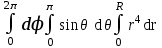 .
.
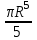 ;
; 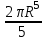 ;
; 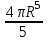 .
.-
Тройной интеграл от единичной функции f(x, y, z) 1 численно равен:
-
Данкриволинейныйинтеграл 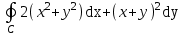 . Вычислить
. Вычислить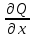 .
.
-
Данкриволинейныйинтеграл 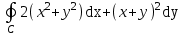 . Вычислить
. Вычислить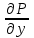 .
.
-
Данкриволинейныйинтеграл 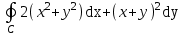 . Вычислить
. Вычислить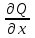 -
-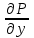 .
.
-
Данкриволинейныйинтеграл 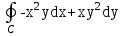 . Вычислить
. Вычислить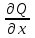 .
.
-
Данкриволинейныйинтеграл 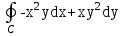 . Вычислить
. Вычислить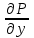 .
.
-
Данкриволинейныйинтеграл 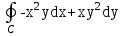 . Вычислить
. Вычислить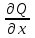 -
- 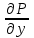 .
.
-
Градиентом скалярного поля u = u (x, y, z) называется вектор:
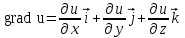 ;
; 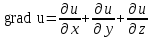 ;
; 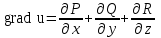 ;
; 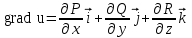 ;
;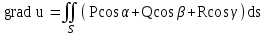 .
.-
Дивергенцией скалярного поля F(M) называется скаляр:
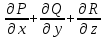 ;
;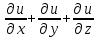 ;
;  ;
; 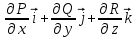 ;
; 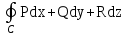 .
.-
Неопределенным интегралом от функции f(x) называется:
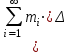 хi;
хi; 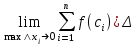 хi;
хi;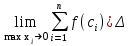 хi;
хi;-
Определенным интегралом от функции f(x) называется:
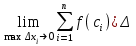 хi
хi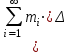 хi
хi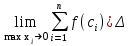 хi
хi-
Продолжитьформулу 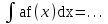
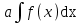 ;
; -
Интеграл  равен:
равен:
 ;
;  ;
;  ;
; -
Интеграл 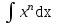 равен:
равен:
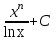 ;
; 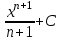 ;
; 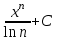 ;
; -
Вычислить 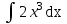 .
.
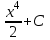 .
.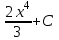 ;
; 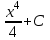 ;
; -
Вычислить 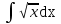 .
.
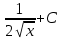 ;
; 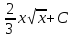 ;
; 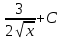 ;
; 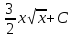 ;
; 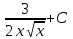 .
.-
Вычислить  .
.
 cos2x + C;
cos2x + C;  cos2x + C;
cos2x + C; -
Вычислить  .
.
 ;
; ;
; ;
;  ;
;  .
.-
Интеграл 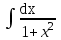 равен:
равен:
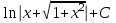 ;
; 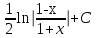 ;
; 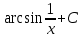
-
Формула интегрирования по частям это:
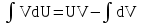 ;
; 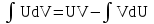 ;
;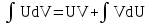 ;
; 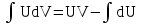 ;
; 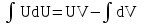
-
Интеграл 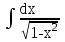 равен:
равен:
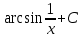 ;
; 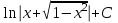 ;
; 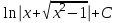 ;
;-
Вычислить 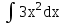 .
.
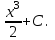
-
Интеграл 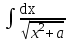 равен:
равен:
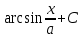 ;
; 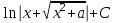 ;
;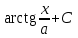 ;
; 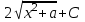 ;
; 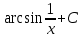
-
Интеграл 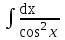 равен:
равен:
-
Интеграл 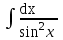 равен:
равен:
-
Каким методом решается интеграл  ?
?
 .
.-
Каким методом решается интеграл 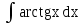 ?
?
 .
.-
Каким методом решается интеграл 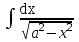 ?
?
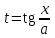 .
.-
Разложение рациональной функции 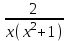 на элементарные дроби имеет вид:
на элементарные дроби имеет вид:
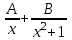 ;
; 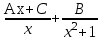 ;
; 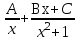 ;
; 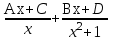 ;
; 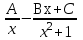
-
Разложение рациональной функции  на элементарные дроби имеет вид:
на элементарные дроби имеет вид:
 ;
;  ;
;  ;
;  ;
; 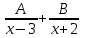
-
Формула Ньютона – Лейбница это:
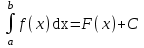 ;
; 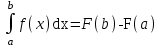 ;
;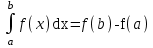 ;
; 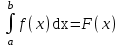
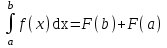 .
.-
Вычислить 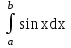 .
.
-
Вычислить  .
.
-
Вычислить 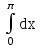 .
.
-
Геометрический смысл определенного интеграла это:
-
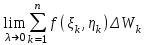 называется:
называется:
-
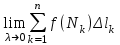 называется:
называется:
-
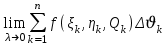 называется:
называется:
-
Если область G-прямоугольник: a 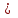 x
x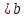 ,
, 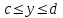 , то
, то 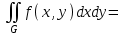
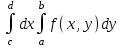
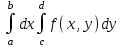
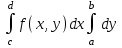

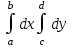
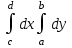
-
Если областьG ограничена снизу и сверху – непрерывными кривыми, слева и справа – прямыми, то 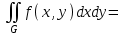
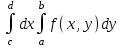
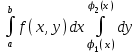
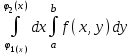
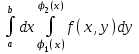
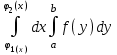
-
Если область G ограничена снизу и сверху- прямыми, слева и справа – непрерывными кривыми, то 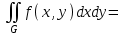
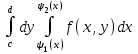
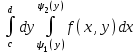
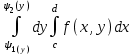
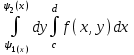
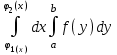
-
Какой интеграл с положительной подынтегральной функцией физически истолковывают как массу соответствующей пластины?
-
Какой интеграл с неотрицательной подынтегральной функцией геометрически истолковывают как объем соответствующего цилиндроида?
-
Какой интеграл с положительной подынтегральной функцией физически истолковывают как массу соответствующего тела?
-
Какой интеграл от единичной функции f(x,y,z) 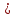 1 численно равен объему области интегрирования?
1 численно равен объему области интегрирования?
-
Как называется выражение  ?
?
-
Как называется выражение  ?
?
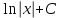
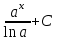
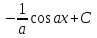
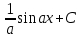
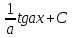
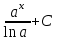
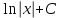
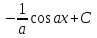
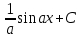
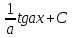
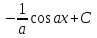
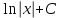
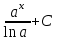
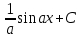
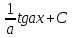
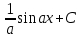
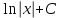
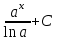
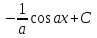
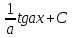
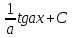
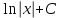
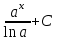
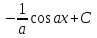
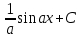
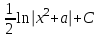
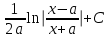

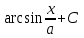
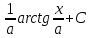
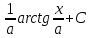
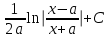

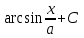
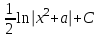
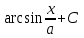
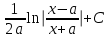

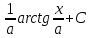
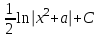

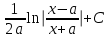
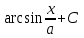
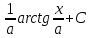
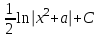
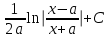

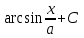
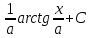
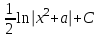
-
Производная функции (x,y)= 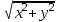 в точке (x0, y0) по направлению вектора
в точке (x0, y0) по направлению вектора 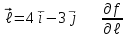 равна:
равна:
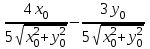
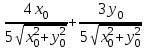
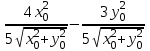
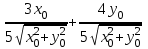
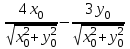
-
Наибольшая скорость возрастания функции (x,y)= 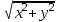 при переходе через точку (3, 4) равна
при переходе через точку (3, 4) равна
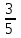
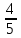
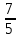
-
Градиент функции u = x2y2z2 в произвольной точке равен

 =(72,36,24)
=(72,36,24)
-
Наибольшая скорость возрастания функции (x, y) = x2 – 2xy + 3y при переходе через точку (1, 2) равна



-
(x, y) = x2 – 2xy + 3y - 1. Тогда градиент 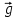 в точке (1, 2) равен
в точке (1, 2) равен
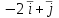
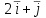
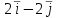
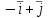
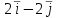
-
Градиент функции u = x2 – y2 + sin z в произвольной точке равен
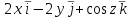

-
Градиент функции u = x2y2z2 в точке (1,2,3) равен
 =(72,36,24)
=(72,36,24) 
-
Производная функции (x, y) = ln (x + y) в точке (1, 2) по направлению биссектрисы первого координатного угла 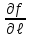 равна
равна
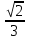
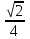
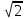
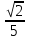
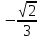
-
Производная функции f(x, y) = x2 + y2 – 4yz в точке (0, 1, 2) по направлению к точке (2, 3, 3) равна
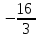
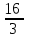
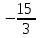
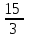
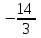
-
Наибольшая скорость изменения функции u(x, y, z) в точке M(x, y, z) равна
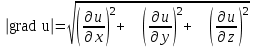
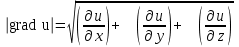
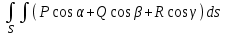
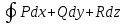

-
Наибольшая скорость возрастания функции (x, y) = 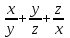 при переходе через точку (-1, 1, -1) равна
при переходе через точку (-1, 1, -1) равна
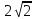
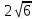

-
Градиент функции (x, y) = 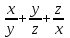 в точке (-1, 1, -1) равен
в точке (-1, 1, -1) равен
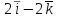
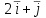
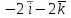
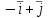
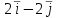
-
Направляющие косинусы вектора 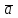 = (2, 2, 1) равны
= (2, 2, 1) равны
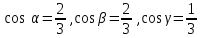
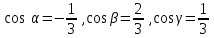
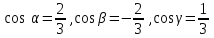
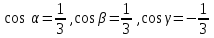
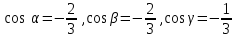
-
Формула 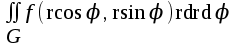 это
это
-
Формула 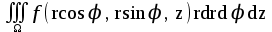 это
это
-
Формула  это
это
-
Найти интеграл 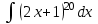 :
:
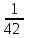 (2х+1)21 + С.
(2х+1)21 + С. (2х+1)21 + С.
(2х+1)21 + С.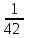 (2х+1)20 + С
(2х+1)20 + С-
Найтиинтеграл 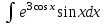 :
:

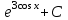 .
.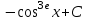 .
.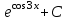 .
. .
.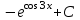 .
.-
Найтиинтеграл 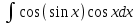 :
:
-
Найтиинтеграл 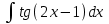 :
:

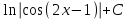 .
.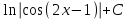 .
.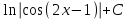 .
.
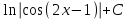 .
.
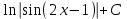 .
.-
Найтиинтеграл 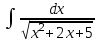 :
:
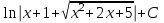 .
.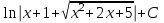 .
.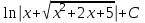 .
.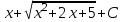 .
.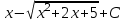 .
.-
Вычислить 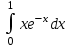 :
:
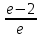 .
.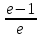 .
.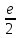 .
.-
Найтиинтеграл 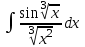 :
:
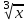 +C.
+C. 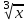 +C.
+C.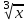 +C.
+C.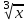 +C.
+C.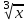 +C.
+C.-
Найти площадь фигуры, ограниченной линиями х = 0, х = , у = 0, у = sinx:
-
Найти площадь фигуры, ограниченной линиями х = 2, у = 0, у = х3:
-
Вычислить 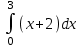 :
:
-
Найтиинтеграл 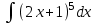 :
:
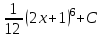 .
.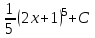 .
.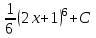 .
.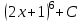 .
.
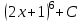 .
.-
Изменить порядок интегрирования: 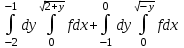
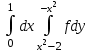
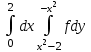
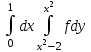
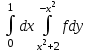
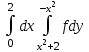
-
Вычислить 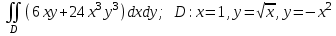 :
:
-
Вычислить 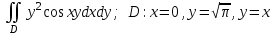 :
:
-
Вычислить 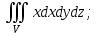
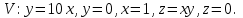
-
Найти площадь фигуры, ограниченной данными линиями 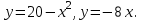
-
Пластинка 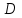 задана ограничивающими ее кривыми,
задана ограничивающими ее кривыми, 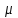 -поверхностная плотность. Найти массу пластинки.
-поверхностная плотность. Найти массу пластинки.
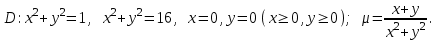
-
Найти объем тела, заданного ограничивающими его поверхностями: 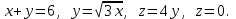
-
Найти объем тела, заданного ограничивающими его поверхностями:
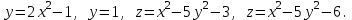
-
Найти объем тела, заданного ограничивающими его поверхностями:
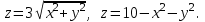
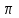
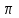
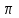
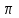
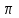
-
Найти объем тела, заданного ограничивающими его поверхностями 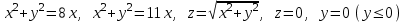 :
:
-
Найти объем тела, заданного ограничивающими его поверхностями 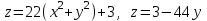 :
:
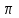
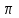
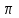
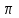
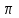
-
Найти объем тела, заданного неравенствами 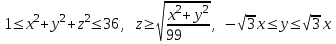 :
:
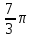
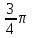
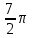
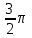
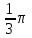
-
Тело 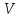 задано ограничивающими его поверхностями,
задано ограничивающими его поверхностями, 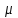 -плотность. Найти массу тела
-плотность. Найти массу тела
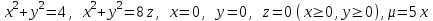 :
: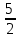
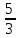
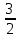
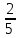
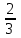
-
Решите уравнение y=y//+y/:
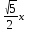 +c2e
+c2e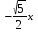 )
) 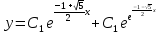
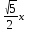 +c2e
+c2e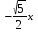 )
) -
Решите дифференциальное уравнение у"-Зу'=0.
-
Найти общее решение y//-5y/+6y=0:
-
Уравнение y’’+k*y’-b*y-sinx=0 – естьуравнение
-
.Решить уравнение первого порядка
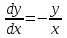
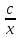
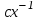
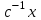
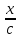
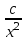
-
Дифференциальное уравнение n-порядка 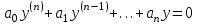
называется:
-
Если два решения однородного уравнения 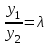 , то
, то
-
Решитеуравнение y’= 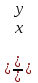 -1
-1
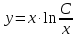
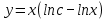
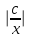
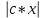
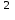 *ln
*ln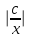
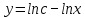
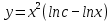
-
Уравнение вида y’’=f(x,y’)
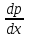 ;
;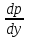 ;
;-
question> Уравнение вида y’+P(x)*y=Q(x)
-
Уравнение вида y’+P(x)*y=Q(x)*y 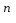 , где n
, где n 0, n
0, n 1,P(x), Q(x) непрерывные функции от х (или постоянные):
1,P(x), Q(x) непрерывные функции от х (или постоянные):
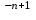
-
С помощью подстановки z = y 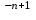 решается
решается
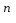 , где n
, где n 0, n
0, n 1
1-
Уравнение вида 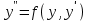 называется Д У, где явно:
называется Д У, где явно:
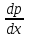 ;
;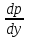 ;
;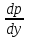 ;
;-
Вычислите: 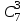
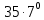
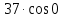
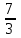
-
Вычислите: 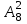
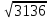
<variant>

-
В урне 18 шаров: 9 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны красный шар?
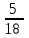
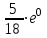
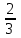

-
В ящике содержится 20 шаров, из них 6 красных, 4 синих и 10 белых. Найти вероятность того, что при случайном вынимании шар окажется цветным.
 .
. 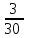 .
. 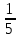 .
. 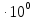
-
Куб, все грани которого окрашены, распилен на тысячу кубиков одинакового размера, которые затем тщательно перемешаны. Найти вероятность того, что наудачу извлеченный кубик будет иметь три окрашенные грани.
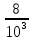
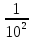
-
В мешочке имеется 5 одинаковых кубиков. На всех гранях каждого кубика написана одна из следующих букв О, П, Р, С, Т. Найти вероятность того , что на вынутых по одному и расположенных в одну линию можно прочесть слово «СПОРТ».
-
При стрельбе из винтовки относительная частота попадания в цель оказалась равной 0,85. Найти число попаданий, если всего было произведено 120 выстрелов:
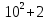
-
В денежно-вещевой лотерее на каждые 10000 билетов разыгрывается 150 вещевых и 50 денежных выигрышей. Чему равна вероятность выигрыша, безразличного или вещевого, для владельца одного лотерейного билета?
-
В партии из 10 деталей 8 стандартных. Найти вероятность того, что среди наудачу извлеченных 2 деталей есть хотя бы одна стандартная.
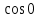
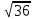
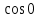
-
Два стрелка произвели по одному выстрелу. Вероятность попадания в мишень первым стрелком 0,7, а вторым 0,6. Найти вероятность того, что хотя бы один из стрелков попал в мишень.
-
У сборщика имеется 16 деталей, изготовленных заводом №1 и 4 детали завода №2. Наудачу взяты 2 детали. Найти вероятность того, что, хотя бы одна из них окажется изготовленной заводом №1
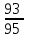
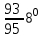
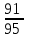
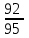
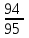
-
В группе спортсменов 20 лыжников, 6 велосипедистов и 4 бегуна. Вероятность выполнить квалификационную норму такова: для лыжника – 0,9; для велосипедиста – 0,8; для бегуна – 0,75. Найти вероятность того, что спортсмен, выбранный наудачу, выполнит норму
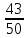
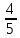
-
В типографии имеется 4 плоскопечатных машины. Для каждой машины вероятность того, что она работает в данный момент равна 0,9. Найти вероятность того, что в данный момент работает хотя бы одна машина
В сосуд емкостью 10 л попала ровно одна болезнетворная бактерия. Какова вероятность зачерпнуть ее при наборе из этого сосуда стакана воды (200см3)
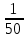
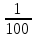
-
Завод отправил на базу 5000 доброкачественных изделий. Вероятность того, что в пути изделие повредиться, равна 0,0002. Найти вероятность того, что на базу прибудут 3 негодных изделия.
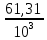
-
16Задумано двузначное число. Найти вероятность того, что задуманным числом окажется случайно названное двузначное число, цифры которого различны.
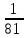
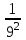
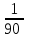
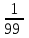
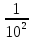
-
Случайная величина Х задана функцией распределения 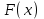 . Найти математическое ожидание случайной величины.
. Найти математическое ожидание случайной величины.
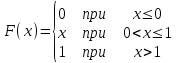


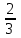

-
Автоматическая телефонная станция получает в среднем 3 вызова в минуту. Вероятность того, что станция получит 6 вызовов за данную минуту, равна